
- •Часть 1
- •Глава I
- •§ 1. Статистическое распределение
- •§ 2. Статистическая независимость
- •§ 3. Теорема Лиувилля
- •§ 4. Роль энергии
- •§ 5. Статистическая матрица
- •§ 6. Статистическое распределение в квантовой статистике
- •§ 7. Энтропия
- •§ 8. Закон возрастания энтропии
- •Глава II
- •§ 9. Температура
- •§10. Макроскопическое движение
- •1) Производную по вектору надо понимать как вектор, составляющие которого равны производным по составляющим вектора, по которому произ- водится дифференцирование.
- •§11. Адиабатический процесс
- •§ 12. Давление
- •§ 13. Работа и количество тепла
- •§ 14. Тепловая функция
- •§ 15. Свободная энергия н термодинамический потенциал
- •§16. Соотношения между производными термодинамических
- •§ 16] Производные термодинамических величин
- •§ 17. Термодинамическая шкала температуры
- •§ 18. Процесс Джоуля — Томсона
- •§ 19. Максимальная работа
- •§ 20. Максимальная работа, производимая телом, находящимся во внешней среде
- •§ 20] Тело, находящееся во внешней среде 77
- •§ 21. Термодинамические неравенства
- •§ 22. Принцип Ле-Шателье
- •§ 23. Теорема Нернста
- •§ 24. Зависимость термодинамических величин от числа частиц
- •§ 25. Равновесие тела во внешнем поле
- •§ 26. Вращающиеся тела
- •§ 27. Термодинамические соотношения в релятивистской области
- •Глава III
- •§ 28. Распределение Гиббса
- •§ 29. Распределение Максвелла
- •§ 30. Распределение вероятностей для осциллятора
- •§ 31. Свободная энергия в распределении Гиббса
- •§ 32. Термодинамическая теория возмущений
- •§ 33. Разложение по степеням %
- •§ 34. Распределение Гиббса для вращающихся тел
- •§ 35. Распределение Гиббса с переменным числом частиц
- •§ 36. Вывод термодинамических соотношений из распределения Гиббса
- •Глава IV
- •§ 37. Распределение Больцмана
- •§ 38. Распределение Больцмана в классической статистике
- •§ 39. Столкновения молекул
- •§ 40. Неравновесный идеальный газ
- •§ 41. Свободная энергия больцмановского идеального газа
- •§ 42. Уравнение состояния идеального газа
- •§ 43. Идеальный газ с постоянной теплоемкостью
- •15. Определить максимальную работу, которую можно получить с по- мощью идеального газа при охлаждении от температуры т до температуры среды т0 при постоянном объеме.
- •§ 44. Закон равнораспределения
- •§ 43. Одноатомный идеальный газ
- •§ 46. Одноатомный газ. Влияние электронного момента
- •§ 47. Двухатомный газ с молекулами из различных атомов. Вращение молекул
- •§ 48. Двухатомный газ с молекулами из одинаковых атомов. Вращение молекул
- •§ 49. Двухатомный газ. Колебания атомов
- •§ 50. Двухатомный газ. Влияние электронного момента
- •§51] Многоатомный газ 169
- •§ 51. Многоатомный газ
- •§ 52. Магнетизм газов
- •Глава V
- •§ 53. Распределение Ферми
- •§ 54. Распределение Бозе
- •§ 55. Неравновесные ферми- и бозе-газы
- •§ 56. Ферми- и бозе-газы элементарных частиц
- •§ 56] Ферми- и бозе-газы элементарных частиц 185
- •§ 57. Вырожденный электронный газ
- •§ 58. Теплоемкость вырожденного электронного газа
- •§ 59. Магнетизм электронного газа. Слабые поля
- •§ 60. Магнетизм электронного газа. Сильные поля
- •§ 61. Релятивистский вырожденный электронный газ
- •§ 62. Вырожденный бозе-газ
- •§ 63. Черное излучение
- •Глава VI
- •§ 64. Твердые тела при низких температурах
- •§ 65. Твердые тела при высоких температурах
- •§ 66. Интерполяционная формула Дебая
- •§ 67. Тепловое расширение твердых тел
- •§ 68. Сильно анизотропные кристаллы
- •§ 69. Колебания кристаллической решетки
- •§ 70. Плотность числа колебаний
- •§ 71. Фононы.
- •§ 72. Операторы рождения и уничтожения фононов
- •§ 73. Отрицательные температуры
- •Глава VII
- •§ 74. Отклонение газов от идеальности
- •§ 75. Разложение по степеням плотности
- •§ 76. Формула ван-дер Ваальса
- •§ 77. Связь вириального коэффициента с амплитудой рассеяния
- •§ 78. Термодинамические величины классической плазмы
- •§ 79. Метод корреляционных функций
- •§ 80. Термодинамические величины вырожденной плазмы
- •1) В этом случае
- •Глава VIII
- •§ 81. Условия равновесия фаз
- •§ 82. Формула Клапейрона — Клаузиуса
- •§ 83. Критическая точка
- •§ 84. Закон соответственных состояний
- •Глава IX
- •§ 85. Системы с различными частицами
- •§ 86. Правило фаз
- •§ 87. Слабые растворы
- •§ 88. Осмотическое давление
- •§ 89. Соприкосновение фаз растворителя
- •§ 90. Равновесие по отношению к растворенному веществу
- •§ 91. Выделение тепла и изменение объема при растворении
- •§ 92. Растворы сильных электролитов
- •§ 93. Смесь идеальных газов
- •§ 94. Смесь изотопов
- •§ 95. Давление пара над концентрированным раствором
- •§ 96. Термодинамические неравенства в растворах
- •§ 97. Кривые равновесия
- •§ 98. Примеры диаграмм состояния
- •§ 99. Пересечение особых кривых поверхности равновесия
- •§ 100. Газ и жидкость
- •Глава X
- •§ 101. Условие химического равновесия
- •§ 102. Закон действующих масс
- •§ 103. Теплота реакции
- •§ 104. Ионизационное равновесие
- •§ 105. Равновесие по отношению к образованию пар
- •Глава XI
- •§ 106. Уравнение состояния вещества при больших плотностях
- •§ 107. Равновесие тел с большой массой
- •§ 108. Энергия гравитирующего тела
- •§ 109. Равновесие нейтронной сферы
- •Глава XII
- •§110. Распределение Гаусса
- •§ 110] Распределение гаусса 365
- •§ 111. Распределение Гаусса для нескольких величин
- •§ 113. Флуктуации в идеальном газе
- •§114. Формула Пуассона
- •§ 115. Флуктуации в растворах
- •§ 116. Пространственная корреляция флуктуации плотности
- •§ 117. Корреляция флуктуации плотности в вырожденном газе
- •§ 118. Корреляция флуктуации во времени
- •§ 119. Временная корреляция флуктуации нескольких величин
- •§ 120. Симметрия кинетических коэффициентов
- •§ 121. Диссипативная функция
- •§ 122. Спектральное разложение флуктуации
- •§ 123. Обобщенная восприимчивость
- •§ 123] Обобщенная восприимчивость 411
- •§ 124. Флуктуационно-диссипационная теорема
- •§ 125. Флуктуационно-диссипационная теорема для нескольких величин
- •§ 126. Операторное выражение обобщенной восприимчивости
- •§ 127. Флуктуации изгиба длинных молекул
- •Глава XIII
- •§ 128. Элементы симметрии кристаллической решетки
- •§ 129. Решетка Бравэ
- •§ 130. Кристаллические системы
- •§ 131. Кристаллические классы
- •§ 132. Пространственные группы
- •§ 133. Обратная решетка
- •§ 134. Неприводимые представления пространственных групп
- •§ 135. Симметрия относительно обращения времени
- •§ 136. Свойства симметрии нормальных колебаний кристаллической решетки
- •§ 137. Структуры с одно- и двумерной периодичностью
- •§ 138. Корреляционная функция в двумерных системах
- •§ 139. Симметрия по ориентации молекул
- •§ 140. Нематические и холестерические жидкие кристаллы
- •§ 141. Флуктуации в жидких кристаллах
- •Глава XIV
- •§ 142. Фазовые переходы второго рода
- •§ 143. Скачок теплоемкости
- •§ 144. Влияние внешнего поля на фазовый переход
- •§ 145. Изменение симметрии при фазовом переходе второго рода
- •§ 146. Флуктуации параметра порядка
- •§ 147. Эффективный гамильтониан
- •§ 148. Критические индексы
- •§ 149. Масштабная инвариантность
- •§ 150. Изолированные и критические точки непрерывного перехода
- •§ 151. Фазовый переход второго рода в двумерной решетке
- •§ 153. Флуктуационная теория критической точки
- •Глава XV
- •§ 154. Поверхностное натяжение
- •§ 155. Поверхностное натяжение кристаллов
- •§ 156. Поверхностное давление
- •§ 157. Поверхностное натяжение растворов
- •§ 158. Поверхностное натяжение растворов сильных электролитов
- •§ 159. Адсорбция
- •§ 160. Смачивание
- •§ 161. Краевой угол
- •§ 162. Образование зародышей при фазовых переходах
- •§ 1Б2] образование зародышей при фазовых переходах 581
- •§ 163. Невозможность существования фаз в одномерных системах
Полученное
в предыдущем параграфе уравнение
состояния (74,6) представляет собой по
существу первые два члена разложения
давления по степеням 1/V:
(75,1)
Первый
член разложения соответствует идеальному
газу. Второй член получается при учете
парного взаимодействия молекул, а в
следующих членах должно участвовать
взаимодействие молекул по три, по
четыре и т. д.2).
Коэффициенты
В,
С, ... в
разложении (75,1) называют вторым,
третьим и т. д. вириальными
коэффициентами.
Для
определения этих величин удобно
начать с вычисления не свободной
энергии, а потенциала Q.
Снова
рассматриваем одноатомный газ и исходим
из общей формулы (35,5), которая в применении
к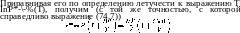
§ 75. Разложение по степеням плотности
![]()
х)
Напомним, что мы рассматриваем слабо
неидеальный газ, т. е. сравнительно''малые
давления. Только в этом приближении
справедлив полученный результат—не
зависящая от давления точка инверсии
(ср. задачу 4 к § 76).
2)
Безразмерным малым параметром, по
которому производится разложение,
является в действительности отношение
Nv0/V
«объема»
одной молекулы v0
к
приходящему на одну молекулу объему
газа V/N.
газу из одинаковых частиц гласит:
со
е-а/г = £ > е,ш/т \e-EN (p. q)/T dYN. (75,2)
Л' = 0 ' J
Мы ввели множитель 1/ЛЧ, после чего интегрирование производится просто по всему фазовому пространству системы Лг частиц (ср. (31,7)).
В последовательных членах суммы по N энергия En (р, q) имеет следующий вид. При N = 0, разумеется, E0(p,q) = 0. При N=1 это есть просто кинетическая энергия одного атома: Ех(р, q) = р212т. При N = 2 она складывается из кинетической энергии двух атомов и энергии их взаимодействия:
2 2
£.(Р.<7) = 2-Ц+^.-
Аналогично
а= 1
где U12i—энергия взаимодействия трех атомов (не сводящаяся, вообще говоря, к сумме (712 + U13 + U2S), и т. д.
Подставим эти выражения в (75,2) и введем обозначение
£ = -^ [e-M»Td,p== (Л^_у-е^ (75 3)
(2я&)3 J И \ 2кР J К
Ниже мы увидим, что это выражение есть не что иное, как
![]()
где Рпд—давление идеального газа при данных Т и V. Получим Q=-rin{ l+lV + ^-^e-^^dV1dV2 +
+ ЩЦе~и,а/7dVidV*dV* + ■ • • }■
Каждая из U12, U12S, ... есть функция только от взаимных расстояний атомов; поэтому, вводя относительные координаты атомов (скажем, относительно первого атома), мы уменьшим кратность интегралов на единицу, получив при этом по лишнему множителю V:
Q=_PV=-Tln{l+|V + -^f Je-iwr dV2 +
Наконец, разлагаем это выражение по степеням £; получающийся ряд может быть представлен в виде
Р = Т%±1", (75,4)
л=1 -
где
J,= \(e-u»>T-l)dVt,
(75 5)
7з== П (е-и"*'т— е~и^т—е-и»'Т—е-и*>'т + 2) dV2dV3
и т. д. Интегралы /„ построены по очевидному закону: подынтегральное выражение в Jп заметно отлично от нуля, лишь если п атомов близки друг к другу, т. е. при столкновении п атомов.
Продифференцировав (75,4) по р, мы получим число частиц в газе, так как
\ф Jt,v \ду. Jt.v
Имея в виду, что согласно определению (75,3) dl/дц = ЦТ, получим
Л^Х-^гЕ». (75,6)
Два уравнения (75,4) и (75,6) определяют в параметрическом виде (параметр |) связь между Р, V и Т, т. е. уравнение состояния газа. Исключая из них £, можно получить уравнение состояния в виде ряда (75,1) с любым желаемым числом членов1).
