§ 62. Вырожденный бозе-газ

При низких температурах свойства бозе-газа не имеют ничего общего со свойствами ферми-газа. Это заранее очевидно из того, что у бозе-газа состоянием наименьшей энергии, в котором газ находится при 7 = 0, должно быть состояние с £ = 0 (все частицы в квантовом состоянии с е = 0), между тем как ферми-газ при абсолютном нуле обладает отличной от нуля энергией.

Если при заданной плотности N/V газа понижать его темпе­ратуру, то химический потенциал р, определяемый уравнением (56,5) (с нижним знаком), будет увеличиваться, т. е., будучи отрицательным, уменьшаться по абсолютной величине. Он достиг­нет значения р. = 0 при температуре, определяемой равенством

N _g(mT)^} Yzdz ^

V 2^1/гяФ.) e^z— 1 *

о

Входящий сюда интеграл выражается через ^-функцию (см. при­мечание на стр. 191); обозначая искомую температуру посред­ством Т₀, получим

При Т <Т₀ уравнение (56,5) не имеет отрицательных решений, между тем как в статистике Бозе химический потенциал должен быть отрицательным при всех температурах.

Это кажущееся противоречие связано с тем, что в данных условиях не законен переход от суммирования (в формуле (54,3)) к интегрированию (в формуле (56,5)). Действительно, при_этом переходе первый член суммы (с e_ft = 0) умножается на ]/е = 0, т. е. выпадает из суммы. Между тем при понижении темпера­туры частицы должны скапливаться именно в этом состоянии с наименьшей энергией, пока при Т = 0 туда не попадут все они. Математически это обстоятельство проявляется в том, что в сумме (54,3) при переходе к пределу р—+0 сумма всех членов ряда, за исключением первого, стремится к конечному пределу (опре­деляемому интегралом (56,5)), а первый член (с е_А = 0) стремится к бесконечности. Устремляя р не к нулю, а к некоторому ма­лому конечному значению, можно, следовательно, придать ука­занному первому члену суммы требуемое конечное значение.

Поэтому в действительности при Т < Т₀ дело будет обстоять следующим образом. Частицы с энергией е > 0 распределены по формуле (56,4) с р = 0:

_dN _ m^8/2V V^de

Полное число частиц с энергиями е > 0 будет, следовательно,

о

Остальные

ЛГ_Е=о = Лг[1-(-^-)^3/2] (62,4)

_р__ёУ(тТГ*Т С о

частиц находятся в низшем состоянии, т. е. имеют энергию е = 0¹). Энергия газа при Т < Т₀ определяется, конечно, только теми частицами, которые имеют е > 0; полагая в (56,7) р. = 0, имеем

gV(mT)^3/2T } z^3/2dz

2^1/2яФ J е^г—1 о

Этот интеграл приводится к £ (5/2) (см. примечание на стр. 191) и получается

/Т \ 3/2 _тЗ/2т.5/2

£ = 0,770Л/Г(-) =0,128g^-^—V. (62,5)

_{С„ = Ш> (62,6)}

Отсюда теплоемкость

(

"° 2Т

т. е. теплоемкость пропорциональна Т^3/2. Интегрируя теплоем- кость, находим энтропию:

S=~, (62,7)

и свободную энергию F — E— TS:

F^-~E. (62,8)

Последний результат вполне естествен, так как при р, = 0 F = (b~PV = Nn+Q = Q. Для давления Р =—(dF/dV)r имеем

_тЗ/2_Г5/2

P = 0,0851g^-_Z_. (62,9)

Мы видим, что при Т < Г₀ давление пропорционально Т^ъ!г и не зависит вовсе от объема. Это обстоятельство—естественное след­ствие того, что частицы, находящиеся в состоянии с е = 0, не обладая импульсом, не дают никакого вклада в давление.

В самой точке Т = Т₀ все перечисленные термодинамические величины непрерывны. Можно, однако, показать, что производная

Явление накапливания частиц в состоянии с е=0 называют конденса­цией Бозе—Эйнштейна. Подчеркнем, что речь может при этом идти разве что о «конденсации в импульсном пространстве», никакой реальной конденсации в газе, конечно, не происходит.

от теплоемкости по температуре испытывает в этой точке скачок (см. задачу к этому параграфу). Кривая самой теплоем­кости как функции от температуры имеет в точке Т = Т₀ излом,

причем в этой точке теплоемкость максимальна (я равна

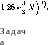Определить скачок производной (dC_v/dT)_v в точке Т = Т₀. Решение. Для решения задачи надо определить энергию газа при малых положительных Т—Т„. Переписываем равенство (56,5) тождественно в виде

N = N₀(T)­

3/2

gVtri

2^1/2п²Р

₁

I

g(e-n)/r_ j

1

1

где функция N₀ (Т) определяется равенством (62,1). Разлагаем подынтегральное выражение, имея в виду, что ц мало вблизи точки Т = Т₀, а поэтому в инте­грале существенна область малых е, и находим, что стоящий здесь интеграл равен

de

KM«+ll*D

-лТ У~Щ.

(1)

Подставляя это значение и выражая затем ц через N—N₀, получим

2л²Р fN₀ — N\²

g²m^s

TV

С той же точностью пишем теперь:

ajj. 2 дц~ 2 ^N ~ 2 °'

откуда

■N

g²m^{s 0} у

TV

fdC_v \ дТ

(2)

где E₀ = E₀ (T)—энергия при ц.=0, т. е. функция (62,5). Вторая производная от второго члена по температуре даст, очевидно, искомый скачок производной теплоемкости. Произведя вычисления, найдем

6я*« Г ( 1 dN₀

g²m^sV²

_{=—3,66^- . г=г0 Т0}

*) Подчеркнем, однако, что такое поведение теплоемкости—результат именно полного пренебрежения взаимодействием частиц газа; ситуация меняется при введении уже хотя бы слабого взаимодействия.

_{Значение}¹ _{производной (dCv/dT)r при Т—Т0—0 есть, согласно (62,5), +2,89N/T0, а при Т = Г0-|-0 оно равно, следовательно, —0,77'N/T0.}