
- •Математические уравнения в геофизике
- •Лабораторная работа 1 (3 часа)
- •Лабораторная работа 2 (3 часа)
- •Лабораторная работа 3 (2 часа)
- •Лабораторная работа 4 (2 часа)
- •Лабораторная работа 5 (2 часа)
- •Лабораторная работа 6 (2 часа)
- •Лабораторная работа 7 (2 часа)
- •Лабораторная работа 8 (2 часа)
- •Лабораторная работа 9 (2 часа)
- •Проверка.
- •Лабораторная работа 10 (2 часа)
- •Лабораторная работа 11 (2 часа)
- •Лабораторная работа 12 (2 часа)
- •Лабораторная работа 13 (3 часа)
- •Лабораторная работа 14 (3 часа)
Лабораторная работа 4 (2 часа)
Задание 1. Матричные операции в MathCad.
Команды Символика – Матрица предназначены для проведения в символьном виде трех наиболее распространенных матричных операций: транспонирование матриц, создание обратных матриц, вычисление определителя матриц. Это команды в подменю Матрица меню Символика обозначены так: Переместить (транспонировать), Инверсировать (обратить), Детерминант (определитель).
Транспонирование матрицы - перестановка строк и столбцов. Подлежащая транспонированию матрица должна быть выделена.
Обращение матрицы – создание такой матрицы А-1, которая при умножении на исходную матрицу А дает единичную матрицу. Обращение допустимо только для квадратных матриц.
Например,
Транспонирование матрицы
Исходное выражение Результат операции
![]()
![]()
![]()
![]()
Обращение матрицы
Исходное выражение Результат операции
![]()

![]()
![]() ·
·![]()
Вычисление детерминанта матрицы
Исходное выражение Результат операции
a·d-b·c
-14
Задание 2. Интегральные преобразования Фурье.
Преобразования Фурье лежат в основе спектрального анализа и синтеза сигналов.
Прямое преобразование Фурье позволяет получить в аналитическом виде функцию частоты F(ω), если задана временная функция f(t). Для этого используется формула:
F(ω)
=
![]()
Обратное преобразование Фурье задается следующей формулой:
f(t)
=
![]()
Для выполнения преобразования Фурье используется команда Трансформация – Фурье меню Символика. Для обратного преобразования Фурье используется команда Трансформация – Инверсная Фурье (обратное преобразование Фурье) меню Символика.
Для выполнения команд преобразования следует записать исходное выражение и выделить в нем переменную, относительно которой будет проводиться преобразование.
Например,
Исходное выражение Результат операции
a·t (прямое преобразование Фурье) 2·1i·π·a·Dirac(1,ω)
2·1i·π·a·Dirac(1,ω) (обратное преобразование) a·t
t+2 (прямое преобразование Фурье) 2·i·π·Dirac(1,ω)+4·π·Dirac(ω)
2·i·π·Dirac(1,ω)+4·π·Dirac(ω) (обратное преобразование) t+2
Задание 3. Интегральные преобразования Лапласа.
Интегральные преобразования Лапласа лежат в основе методов расчета электрических цепей. Эти преобразования позволяют легко решать линейные дифференциальные уравнения. В этих преобразованиях фигурирует оператор Лапласа, который обозначается в в идее s = jw (иногда он обозначается как р). Оператор Лапласа позволяет переходить от уравнений с комплексными величинами к уравнениям с действительными величинами. Для выполнения этих преобразований служат команды Трансформация – Лапласа и Трансформация –Инверсная Лапласа меню Символика.
Прямое преобразование Лапласа позволяет по известной временной функции f(t) найти передаточную функцию F(s) по формуле:
F(s)
=
![]() .
.
Обратное преобразование Лапласа позволяет по передаточной функции F(s) найти временную функцию f(t) по формуле:
f(t)
=
![]()
Выражение F(s) должно иметь особенности слева от линии Re(s) = s.
Например,
Исходное выражение Результат операции
1-exp(-![]() (прямое преобразование)
(прямое преобразование)
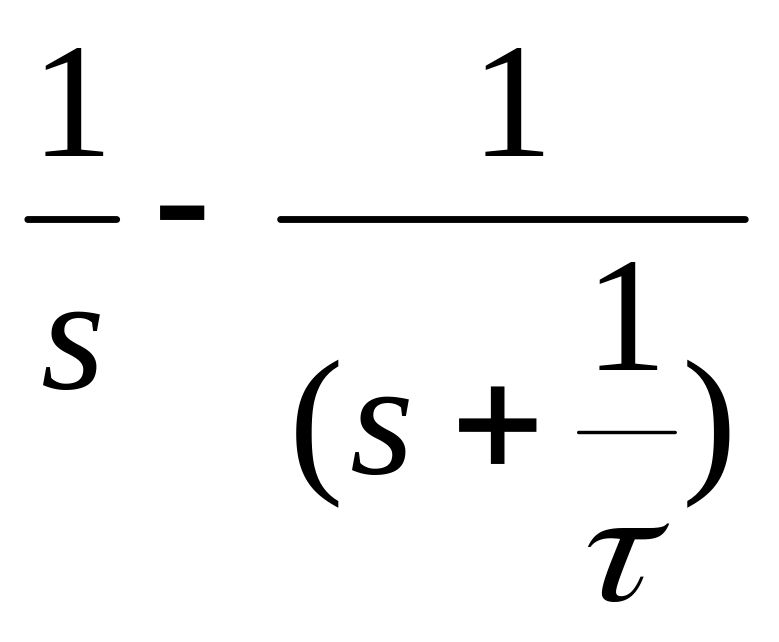
(обратное
преобразование)
![]()
Результат обратного преобразования не всегда приводит к первоначальному результату.
1-t (прямое
преобразование)
![]()
(обратное преобразование) 1-t
Задание 4. Интегральные Z - преобразование.
Применяются в теории автоматического управления и в различных сферах прикладной математики.
Прямое Z – преобразование реализуется выражением:
F(z)
=
![]() .
.
Обратное Z – преобразование соответствует контурному интегралу:
f(n)
=
![]() .
.
Для выполнения этих преобразований служат команды Трансформация – Z и Трансформация –Инверсная Z меню Символика.
Например,
Исходное выражение Результат операции
a·n
(прямое преобразование)
a·![]()
a· (обратное преобразование) a·n
Задание 5. Символьные операции с применением оператора символьного вывода.
Специальный оператор символьного вывода имеет вид удлиненной горизонтальной стрелки, направленной вправо. Этот оператор можно вызвать нажатием комбинации клавиш Ctrl + . (точка) или из палитры математических символов (Панели ключевой символики).
В шаблоне оператора символьного вывода имеется место ввода, куда необходимо ввести исходное выражение. Если задать исходное выражение и вывести курсор из формульного блока, то после оператора символьного вывода система выведен результат символьных преобразований.
Используется также расширенный оператор символьного вывода, который задается нажатием комбинации клавиш Ctrl + Shift + . или выбором из палитры символьных операций (Панели ключевой символики).
В шаблоне оператора имеется два места ввода. В первое вводится исходное выражение, а во второе – одна из директив символьных преобразований. Директивы символьных преобразований задаются либо вводом соответствующих ключевых слов, либо выбором из палитры символьных операций.
Директивы символьного оператора.
- simplify – упрощение выражений;
- expand – разложение выражения по степеням;
- factor – разложение выражения на простые дроби;
- complex – преобразование в комплексной форме;
- assume – присваивание переменным определенного значения, а также задание ограничения на значения или тип переменных;
- series – разложение в ряд по заданным переменным;
- float – преобразование в формат чисел с плавающей точкой;
- literally - запрет символьного преобразования для последующего выражения;
- parfrac – разложение на элементарные дроби;
- coeffs – возвращение вектора с коэффициентами полинома;
- fourier – прямое преобразование Фурье;
- laplace – прямое преобразование Лапласа;
- ztrans – прямое Z – преобразование;
- infourier – обратное преобразование Фурье;
- invlaplace – обратное преобразование Лапласа;
- invztrans – обратное Z – преобразование;
- MT → - транспонирование матрицы;
- M-1 → - инвертирование матрицы;
- |M| → - вычисление детерминанта матрицы;
- Modifier – модифицированные команды:
- assume - вводное слово для приведенных ниже определений;
- real – для var = real – означает вещественное значение переменной var;
- RealRange – для var = RealRange(a, b) – означает принадлежность вещественной переменной var к интервалу [a, b];
- trig – задает направление тригонометрических преобразований.
Например,

