4. Теплопроводность (6 часов).

Лекция 7. Одномерная стационарная теплопроводность. Простые аппроксимации профилей и предположение о виде профиля. Дискретный аналог. Основные принципы выбора интерполяционных функций и профилей.

Лекция 8. Нестационарная одномерная теплопроводность. Обобщенный дискретный аналог. Явная, Кранка-Николсона и полностью неявная схемы. Двух- и трехмерные задачи нестационарной теплопроводности. Дискретный аналог для двух и трех измерений. Особенности дискретных аналогов не в ПДСК.

Лекция 9. Итерационные методы решения системы линейных уравнений. Поточечный последовательный метод Гаусса-Зейделя. Критерий Скарбороу. Метод переменных направлений (полинейный метод). Методы верхней и нижней релаксации. Использование коэффициента релаксации. Релаксация с использованием инерции.

+ Особенности дискретных аналогов не в ПДСК.

Одномерная стационарная теплопроводность 4-1

Простые аппроксимации профилей 4-1

Предположение о виде профиля 4-1

Дискретный аналог 4-2

Основные принципы выбора интерполяционных функций и профилей 4-2

Нестационарная одномерная теплопроводность 4-3

Обобщенный дискретный аналог 4-3

Явная, Кранка-Николсона и полностью неявная схемы 4-4

2D и 3D нестационарная теплопроводность 4-6

Дискретный аналог для двух измерений 4-6

Дискретный аналог для трех измерений 4-7

Особенности дискретных аналогов не в ПДСК 4-7

Итерационные методы 4-8

Решение алгебраических уравнений 4-8

Поточечный последовательный метод Гаусса - Зейделя 4-9

Критерий Скарбороу 4-10

Метод переменных направлений (полинейный метод) 4-11

Методы верхней и нижней релаксации 4-12

Использование коэффициента релаксации 4-12

Релаксация с использованием инерции 4-13

Одномерная стационарная теплопроводность

Рассмотрим стационарную задачу теплопроводности, описываемую уравнением

, (4.1)

где S – скорость выделения тепла в единице объема.

Для получения дискретного аналога будет использовано показанное на рис. 4.1 расположение точек. В центре точка P (Point - точка), соседние точки W (West – запад, направление обратное оси х, против потока) и Е (East – восток, направление вдоль оси х, по потоку).

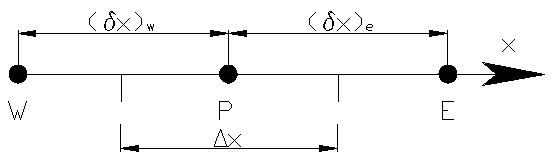
Рис. 4.1 Схема расположения точек для одномерного дискретного аналога

Объем показанного КО: х*1*1 (размеры вдоль y и z равны 1).

Интегрируем по КО получаем

Простые аппроксимации профилей

На рисунках 4.2 и 4.3 показаны соответственно ступенчатый и кусочно-линейный профиль, которые являются простейшими аппроксимациями более сложных функций.

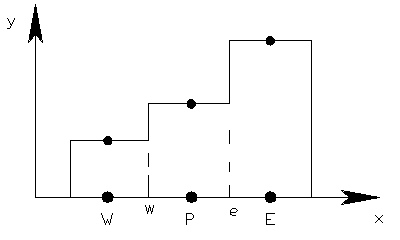
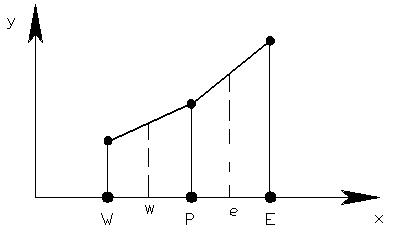
Рис. 4.2 Ступенчатый профиль Рис. 4.3 Кусочно-линейный профиль

Предположение о виде профиля

Сделаем теперь предположение о виде профиля или интерполяционной формулы. На рис. 4.2 и 4.3 показаны два простых профиля. В простевшем случае предполагается, что значение T в узловой точке сохраняется для всего окружающего ее контрольного объема. Это предположение приводит к показанному на рис. 4.2 ступенчатому профилю. Для такого профиля производная dT/dx на границах КО (т.е. в точках w или е) не определена. Эта трудность не возникает для кусочно-линейиого профиля, у которого изменение Т между узловыми точками описывается линейными интерполяционными функциями (см. рис. 4.3).