3. Угловые соотношения между плоскостями

Рассмотрим две плоскости, определяемые общими уравнениями:

А₁х + В₁у + С₁z + D₁ =0, А₂х + В₂у + С₂z + D₂ =0.

У глом между двумя плоскостями называется любой из двух смежных двугранных углов, образованных этими плоскостями (рис. 11.10).

Один из указанных двугранных углов равен углу между нормальными векторами к соответствующим плоскостям:

={А₁, В₁, С₁}

и ={А₂, В₂, С₂}.

Эти векторы можно построить из общего начала. Второй двугранный угол будет смежным с ним.

Следовательно, . (11.5)

Пример 11.3. Найти двугранные углы, образованные пересечением плоскостей х – у + z – 3 = 0, х + у – z + 4 = 0.

Решение. Один из искомых двугранных углов равен углу между нормальными векторами = {1, – , 1}, = {1, , –1} к рассматриваемым плоскостям. Находим его по формуле (11.5):

, ₁ = .

Другой двугранный угол равен .

Условие параллельности двух плоскостей

П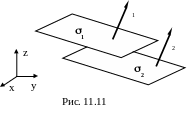 лоскости, определяемые общими уравнениями, параллельны, очевидно, тогда и только тогда, когда их нормальные векторы и коллинеарны (рис. 11.11).

Условием коллинеарности двух векторов служит пропорциональность их соответствующих координат. Следовательно, необходимым и достаточным признаком параллельности двух плоскостей, определяемых общими уравнениями, служит равенство .

Условие перпендикулярности двух плоскостей

Плоскости, определяемые общими уравнениями вида (11.3), перпендикулярны тогда и только тогда, когда их нормальные векторы и перпендикулярны (рис. 11.12).

Условием перпендикулярности двух векторов служит равенство нулю их скалярного произведения:

Таким образом, необходимым и достаточным условием перпендикулярности двух плоскостей служит равенство A₁A₂ + B₁B₂ + C₁C₂ = 0.

П ример 11.4. Определить, при каком значении  плоскости

₁: 2х + у – 3z – 4 = 0 и

₂: х + у – 3z – 8 = 0

будут перпендикулярны.

Решение. Координатами нормальных векторов плоскостей ₁ и ₂ будут коэффициенты при х, у и z:

₁ = {2, , -3}, ₂ = { , 1, -3}.

Тогда по условию _{1 2} = 0 получим: 2 +  + 9 = 0, отсюда  = - 3.

Вопросы на понимание основных понятий:

1. По какой формуле вычисляется угол между двумя плоскостями?

2. Каково условие параллельности двух плоскостей?

3. Каково условие перпендикулярности двух плоскостей?

4. Уравнения прямой а) Канонические уравнения прямой в пространстве

П усть в пространстве R³ задана прямая L. Всякий отличный от нуля вектор = {, m, n}, коллинеарный прямой L, т.е. параллельный прямой или лежащий на ней, называется направляющим вектором этой прямой, а его координаты , m, n – направляющими коэффициентами прямой (рис. 11.13).

Через данную точку M₀(x₀, y₀, z₀) можно провести единственную прямую L, параллельную вектору .

Составим уравнение этой прямой. Пусть M(x, y, z) произвольная точка пространства. Обозначим через радиус-векторы точек M₀(x₀, y₀, z₀), M(x, y, z) соответственно. Точка M(x, у, z) будет лежать на прямой L тогда и только тогда, когда вектор будет коллинеарен вектору , и, следовательно, (11.6),

где скалярный множитель t, называемый параметром, может принимать любые действительные значения в зависимости от положения точки M на прямой L.

Из выражения (11.6) очевидно, что . (11.7)

Это равенство выражает закон изменения радиуса вектора точки M, перемещающейся вдоль прямой L по мере изменения параметра t. В связи с этим его называют векторным уравнением прямой L, проходящей через данную точку параллельно вектору

Если параметр t рассматривать как время, то векторному уравнению (11.7) можно дать физическую интерпретацию. Записав его в равносильной форме (11.6), видим, что за единицу времени t = 1 (например за 1 секунду) точка M, двигаясь вдоль прямой L, получит приращение, равное вектору . Следовательно, векторное уравнение (11.7) выражает закон прямолинейного движения точки M со скоростью ; модуль этой скорости равен модулю вектора : .

Если все координаты направляющего вектора прямой не равны нулю, , m  0, n  0, то условие коллинеарности векторов и мы можем записать в виде

. (11.8)

Условимся записывать равенства (11.8) и в том случае, когда одно или два из чисел , m, n равны нулю, считая в этом случае и соответствующий числитель равным нулю.

Уравнения (11.8) называются каноническими уравнениями прямой линии, проходящей через точку M₀(x₀, y₀, z₀) и имеющей направляющий вектор .