МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БАШКОРТОСТАН

Государственное бюджетное образовательное учреждение

среднего профессионального образования

«Уфимский механико-технологический колледж»

Методическая разработка

Методические указания по

выполнению самостоятельных работ

по дисциплине ''Математика''

для студентов 1 курса

специальностей:

140448 «Техническая эксплуатация и обслуживание электрического и электромеханического оборудования (по отраслям)»,

151022 «Монтаж и техническая эксплуатация холодильно-компрессорных машин и установок (по отраслям)»,

151031 «Монтаж и техническая эксплуатация промышленного оборудования (по отраслям)»,

260101 «Технология хранения и переработки зерна»,

260103 «Технология хлеба, кондитерских и макаронных изделий»,

260107 «Технология бродильных производств и виноделия»,

260113 «Технология консервов и пищеконцентратов»,

260201 «Технологии молока и молочных продуктов»,

260807 «Технология продукции общественного питания»,

080114 «Экономика и бухгалтерский учет (по отраслям)»,

100801 «Товароведение и экспертиза качества потребительских товаров»

Разработал:	Преподаватель	________________________ (Подпись)	Т.И. Казыханова О.В. Седова А.В. Хасанова (И.О.Фамилия)	____________ (Дата)
Согласовано:	Председатель ПЦК ФМД и ИКТ _____________________________	(Подпись)	Э.Р. Усманова (И.О.Фамилия)	____________ (Дата)

2014 г.

Содержание

Y

I Общие рекомендации по выполнению самостоятельных работ 2

II Самостоятельная работа 3

Раздел 1. Алгебра и элементарные функции 3

Виды колебаний 7

Уравнение гармонического колебания 8

1. Вычислить предел числовой последовательности: 10

2. Вычислить предел числовой последовательности: 11

3. Вычислить предел числовой последовательности: 11

4. Вычислить предел числовой последовательности: 11

5. Вычислить предел числовой последовательности: 12

6. Вычислить предел числовой последовательности: 12

7. Вычислить предел числовой последовательности: 13

8. Вычислить предел числовой последовательности: 13

9. Вычислить предел числовой последовательности: 14

10. Вычислить предел числовой последовательности: 14

11. Вычислить предел числовой последовательности: 14

Раздел 2. Начала математического анализа 17

Раздел 3. Геометрия 39

Раздел 4. Элементы теории вероятностей и математической статистики 126

Правила при написании доклада 127

Литература 133

I Общие рекомендации по выполнению самостоятельных работ

В соответствии с рабочим и календарно-тематическим планом студенты первого курса на базе основного общего образования при изучении математики выполняют самостоятельные работы в объеме 90 часов, в том числе: реферат – 8 часов, составление кроссворда – 8 часов, работа с книгой - 74 часа. Предусматриваются различные виды самостоятельной учебной деятельности: подготовка устных сообщений, решение задач определенной тематики, изучение тем по учебникам и конспекту, разработка кроссвордов, рефератов по темам изучаемой дисциплины.

Перед выполнением заданий студент должен руководствоваться следующим:

1. Самостоятельную работу необходимо выполнить или сдать на проверку в срок, установленный преподавателем.

2. Перед выполнением самостоятельной работы студенту следует изучить конспект, соответствующие разделы учебной литературы.

3. При затруднениях, возникших при выполнении самостоятельной работы, студент может получить консультацию преподавателя, в том числе по интернету в специально группе.

II Самостоятельная работа Раздел 1. Алгебра и элементарные функции

(Самостоятельная работа 24 час.)

1.1. Составление кроссвордов по теме «Степени и логарифмы» (4 часа).

По словарю русского языка Ожегова «кроссворд – игра-задача, в которой фигуру из квадратов нужно заполнить буквами, составляющими пересекающиеся слова».

Кроссворды – это гимнастика ума и испытание на эрудицию. Вряд ли есть люди, которые не разгадывали кроссворды. Для многих это становится любимым развлечением и часто приводит к тому, что человек начинает сам составлять кроссворды.

Оптимальный вариант – это выбрать сетку и начать ее заполнять. При обретении достаточного опыта, можно пойти и от обратного: то есть, сетку строить потом, но это достаточно сложно – нужно симметрично располагать слова и т.д.

Если сложно нарисовать сетку самостоятельно, то легко можно взять сетку из любого печатного издания – стандартную классическую черно-белую сетку разных конфигураций.

Первый совет: надо обратить внимание на количество пересечений. Самое простое – это когда слова пересекаются в двух, максимум – в трех местах. Больше – это будет намного сложнее, особенно к концу кроссворда. Допустим, сетка с двойным или тройным пересечением слов выбрана, и теперь надо перейти к ее заполнению.

Совет второй: старайтесь, чтобы в местах пересечений оказались гласные. Составить пересекающееся слово в варианте «-а-и-а» гораздо легче, чем «-к-с-н». Если все же в пересечении попали согласные, то желательно выбирать легко сочетаемые и часто встречающиеся, например, «к», «р», «с». В предпоследнее пересечение можно поставить «н» или «к».

Естественно, обычно в кроссворде встречается несколько длинных слов и много-много слов из 5-ти или 4-х букв.

Совет третий: придумать сначала длинные слова, состыковать их друг с другом, а уж затем подгонять под них короткие. Выбор оригинальных слов из трех букв довольно невелик, и поэтому они, по техническим причинам, кочуют из одного кроссворда в другой. Наиболее интересные слова лучше заполнять сначала – потом, к концу сетки, придется элементарно подгонять их по уже имеющемуся в наличии сочетанию букв, а в начале пути еще есть полный простор.

Наиболее трудно составляемые из всех – это тематические кроссворды. Сначала нужно выписать или вспомнить максимум слов, которые относятся к данной теме, например, «Степени и логарифмы».

Определения к кроссвордам должны быть разнообразными, например, «животное с картины Леонардо да Винчи» – горностай (имеется в виду знаменитая «Дама с горностаем») и т.д. Именно определения делают кроссворд интересным и захватывающим, потому что знание географии и зоологии – это одно, а способность к ассоциативному мышлению – это другое.

1 шаг

Для начала нам необходимо составить вопросы и правильно их сформулировать. Это дело не хитрое и для успешного создания вопросов нужно помнить только 3 правила: 1) Составляем несложные вопросы, с недлинным ответом. 2) Ответ должен состоять из одного слова без наличия в нём дефиса и других знаков, в именительном падеже. 3) Разделите ответы на горизонтальные и вертикальные.

2 шаг

Далее составив вопросы с ответами, запускаем Excel и записываем ответы в виде кроссворда, вам понадобится лишь дизайнерский талант. Аккуратно составив, далее мы выделяем всю область где находится кроссворд и окружаем его в рамку (Выделяем диапазон – границы – внешние границы). Теперь те строки и столбцы где будут ответы, мы выделяем по очереди и выбираем Границы – Все границы. Теперь у Вас есть поле с выделенными местами для ответов, для более красивого внешнего вида, выделите те ячейки в которых нет ответа и поставьте свой цвет заливки. Наиболее подходит серый цвет (Белый фон, более тёмный оттенок 15%).

3 шаг

Для того чтобы все ячейки уменьшить или увеличить и задать одинаковый размер выделенному диапазону, мы его выделяем и заходим по следующему адресу: Для изменения размера строки – Формат – Строка – Ширина строки (На мой вкус лучше ставить значение 20). Для изменения размера столбца – Формат – Столбец – Ширина столбца (На мой вкус лучше ставить значение 4).

4 шаг

Далее нумеруем ячейки. Первая буква ответа должна иметь номер это вопроса. Лучше всего выбирать восьмой размер шрифта и шрифт Calibri. Ну вот и всё. В принципе дело не хитрое, но немного подумать стоит. Всем удачи и успехов.

Задание. Составить кроссворд по теме «Степени и логарифмы», содержащий не меньше 10 слов. Оформить на листе формата А4.

Основные свойства степени. Если а и b — положительные, а

— любые действительные числа, то

1) а° = 1;

2)

3)

4)

5)

6)

Логарифмом положительного числа b по основанию а (а > 0; а # 1) называется показатель степени, в которую нужно возвести основание а, чтобы получить b.

Обозначение:

log_ab (Iog₁₀ b = lg b, log_eb = In b).

Определение логарифма записывается в виде равенства

a^log_a^b = b

которое называется основным логарифмическим тождеством. Из этого тождества и свойств степени вытекают следующие свойства логарифмов:

1) log_a(b₁b₂) = log_a b₁ + log_a b₂

2)

3)

4)

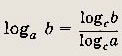
5) log_a х² = 2log_a| x|.