П рактическое задание

Вариант 1

1. Запишите элемент С₂₄ матрицы С

2. Вычислите минор М₄₄

3. Вычислить алгебраическое дополнение С₁₁

4. Вычислить произведение элементов главной диагонали

5. Разложите определитель по 3-й строчке, не вычисляя полученные определители.

6. Разложите определитель по 2 –у столбцу, через алгебраические дополнения (не вычисляя).

Вариант 2

1. З апишите элемент Е₁₄ матрицы Е

2. Вычислите минор Е₂₃

3. Вычислить алгебраическое дополнение Е₃₁

4. Вычислить произведение элементов побочной диагонали

5. Разложите определитель по 2-й строчке, не вычисляя полученные определители.

6. Разложите определитель по 4 –у столбцу, через алгебраические дополнения (не вычисляя).

Вариант 3

1 . Запишите элементD₁₂ матрицы D

2. Вычислите минор D₃₁

3. Вычислить алгебраическое дополнение D₂₃

4. Вычислить произведение элементов побочной диагонали

5. Разложите определитель по 1-й строчке, не вычисляя полученные определители.

6. Разложите определитель по 3 –у столбцу, через алгебраические дополнения (не вычисляя).

Вариант 4

1. З апишите элемент F₂₂ матрицы F

2. Вычислите минор F₄₁

3. Вычислить алгебраическое дополнение F₁₄

4. Вычислить произведение элементов главной диагонали

5. Разложите определитель по 4-й строчке, не вычисляя полученные определители.

6. Разложите определитель по 1 –у столбцу, через алгебраические дополнения (не вычисляя).

Практическое занятие № 2 Решение систем линейных уравнений по формулам Крамера.

Тема программы: Системы линейных уравнений

Цель работы: научиться решать системы линейных уравнений по формулам Крамера.

Время выполнения: 2 часа.

Теоретические основы

Определители впервые были введены для решения системы уравнений первой степени. В 1750г. швейцарский математик г. Крамер дал общие формулы, выражающие неизвестные через определители, составленные из коэффициентов системы.

Рассмотрим систему трех уравнений первой степени с тремя неизвестными :

(коэффициенты 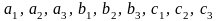и свободные члены считаются заданными).

Тройка чисел называется решением системы , если в результате подстановки этих чисел вместо все три уравнения обращаются в тождество.

В дальнейшем основную роль будут играть следующие четыре определителя:

Определитель называется определителем системы . Определители , , получаются из определителя системы заменой свободными членами элементов соответственно первого, второго и третьего столбцов.

Возможны три случая:

1) Если определитель системы отличен от нуля ( ), то существует, и притом единственное, решение этой системы и оно выражается формулами (формулы Крамера)

2) Если определитель системы равен нулю ( ) и хотя бы один из определителей , , отличен от нуля, то система не имеет решения (несовместна).

3) Если и , то система либо совсем не имеет решений, либо если система имеет хотя бы одно решение, то она имеет бесконечно много решений. В этом случае, одно из трех уравнений является следствием двух других. Система сводится к двум уравнениям с тремя неизвестными и имеет бесчисленное множество решений.