ГБОУ СПО «Серпуховский машиностроительный техникум МО»
Дисциплина «Элементы высшей математики»
Раздел 1. Элементы линейной алгебры.
1. Линейные действия над матрицами и их свойства
Определение
Числовой
матрицей (матрицей) размера
будем называть прямоугольную таблицу
чисел, содержащую
строк и
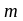столбцов, и обозначать
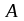или
.
Матрица
,
содержащая один столбец, называется
столбцом.
Матрица
,
содержащая одну строку, называется
строкой.
Столбцы
и строки будем обозначать как векторы
-
.
Пример.
Матрица
содержит свои элементы в 3-х строках и
3-х столбцах.
Обозначение:
=
или
= |
|,
=1,2,3,
=1,2,3
- обозначение элемента матрицы, расположенного в -й строке, и -м столбце, ( =1,2,3, =1,2,3);
- индекс, указывающий номер строки;
- индекс, указывающий номер столбца.
Линейными действиями над матрицами называются операции сложения матриц, и умножения матрицы на число.
Определение
При
сложение матриц
и
образуется матрица
,
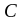каждый элемент которой равен сумме
соответствующих элементов матриц
и
.
Обозначение суммы матриц: = +
где
=|
|,
=|
|,
=|
|,
=
+
,
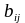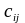=1,…,n,
=1,…,m.
Пример
№.
+
=
Определение
При
умножении матрицы
на
образуется матрица
,
каждый элемент которой равен произведению
соответствующего элемента матрицы
на
.
Обозначение
произведения матрицы на число:
=
где =| |, =| |, = , =1,…,n, =1,…,m, .
Пример.
3
=
Определение
Линейной
комбинацией столбцов
с коэффициентами
называется выражение вида:
=
Пример.
Столбец
=
является линейной комбинацией столбцов
=
и
=
с коэффициентами 1, 2.
линейно
выражается через
и
:
=
+ 2
=
=
+2
.
Аналогично
вводится понятие линейной комбинации
матриц
с коэффициентами
:
=
.
Линейные свойства матриц:
Пусть
=|
|,
=|
|,
=1,…,n,
=1,…,m,
,
,
тогда:
1.A + B = B + A (коммутативность)
2.(A + B) + C = A + (B + C) (ассоциативность)
3. (A + B) = A + B (дистрибутивность)
4.(
+
)A
=
A
+
A
(дистрибутивность)
5.( )A= ( A) (ассоциативность)
2. Произведение матриц и их свойства
Определение.
Произведением
матриц
и
называется матрица
,
элементы которой определяются по формуле:
=
,
(
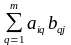=1,…,n,
=1,…,k
).
Обозначение
:
=
,
=|
|.
Пример. Пусть , . Найти = .
=
=
+
+…+
,
=
=
+
+…+
,
=
=
+
+…+
,
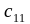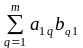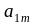
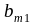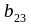и т.д.
Матрицы и можно перемножить, если число столбцов матрицы (т.е. длина строки матрицы ) равно числу строк матрицы (т.е. длине столбца матрицы ).
Количество строк матрицы ( где = ) определяется количеством строк матрицы , а количество столбцов – количеством столбцов матрицы B.
Пример.
=
=
=
3
1
+ 1
0
+ 0
1
+ 2
3
= 9
= 6
1
+ 2
0
+ 0
1
+ 4
3
= 18
=
3
2
+ 1
3
+ 0
7
+ 2
0
= 9
= 6
2
+ 2
3
+ 0
7
+ 4
0
= 18
=
3
7
+ 1
0
+ 0
9
- 2
6
= 9
= 6
7
+ 2
0
+ 0
9
- 4
6
= 18
Свойства произведения матриц:
1.
=
(ассоциативность)
2.
=
+
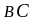(дистрибутивность)
В
общем случае произведение матриц не
коммутативно, т.е.
.
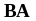Если = , тогда матрицы и называются перестановочными.
Пример.
Умножим
матрицу
=
на столбец
=
=
=
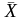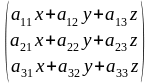
Матричной записью системы линейных уравнений
называется
выражение вида:
=
,
или кратко:
=
,
где:
= - матрица системы;
= - столбец неизвестных; = - столбец свободных членов.