
- •Второе начала термодинамики. Энтропия.
- •Свойства энтропии
- •Цикл карно
- •Соотношение первого и второго начал термодинамики
- •Изменение энтропии в различных процессах в закрытой системе
- •Контрольные вопросы
- •Формулировка второго начала тд :Что такое Энтропия?
- •Свойства энтропии
- •Соотношение I и II начал тд: ∆Uобр
- •Третье начало термодинамики
- •Характеристические функции. Термодинамические потенциалы
- •Термодинамические условия самопроизвольного протекания процесса и достижения состояния равновесия
- •Контрольные вопросы
дЛекция №4.1
Второе начала термодинамики. Энтропия.
Второе начало (второй закон) термодинамики определяет направление, условия и пределы самопроизвольного протекания процессов (без затраты энергии извне).
Второе начало термодинамики имеет статистический (вероятностный) смысл, т.е. применимо к системам, состоящим из большого числа частиц, и определяет наиболее вероятное направление самопроизвольного протекания процесса в данных условиях.
Существуют различные эквивалентные формулировки второго начала термодинамики:
а) Теплота не может самопроизвольно переходить от более холодного тела к более горячему.
б) Невозможен процесс, единственным результатом которого было бы превращение теплоты в работу или вечный двигатель второго рода невозможен.
Вечный двигатель (перпетуум мобиле) второго рода — воображаемая периодически действующая тепловая машина, целиком превращающая в работу теплоту, переданную окружающей средой.
в) Математическая формулировка. Введем функцию состояния S системы функцию энтропия системы. Определим эту функцию следующим образом.
Для обратимого изотермического процесса
dS =Q/T, ∆S = Q/T,
где dS и ∆S — соответственно бесконечно малое и конечное изменение энтропии; Q и Q - бесконечно малая и конечная величина теплоты, переданной системе окружающей средой; Т - абсолютная температура системы; Q/T и Q/T- соответственно элементарная приведенная теплота и приведенная теплота.
Для необратимого изотермического процесса
dS > Q/T, ∆S>Q/T
Эти соотношения выражают математическую формулировку второго начала термодинамики. В общем случае dS > Q / Т , ∆S > Q / Т/
Свойства энтропии
Энтропия S - экстенсивная функция состояния системы, приращение которой в обратимом процессе при постоянной температуре равно отношению теплоты Q процесса к температуре Т, т.е. приведенной теплоте процесса Q / Т.
Единицы измерения молярной энтропии - Дж/моль . К
В изолированной системе самопроизвольно протекают процессы, сопровождающиеся увеличением энтропии. С ростом температуры энтропия системы увеличивается.
Понятие энтропия имеет многогранный физический смысл:
1)Энтропия — функция состояния системы, изменение которой в обратимом бесконечно малом изотермическом процессе равно приведенной теплоте процесса.
Энтропия — функция состояния системы, являющаяся производной от энергии Гиббса по температуре с отрицательным знаком (при постоянном давлении) или производной от энергии Гельмгольца по температуре с отрицательным знаком (при постоянном объеме).
Энтропия — мера разупорядоченности (хаотичности) системы. Чем больше разупорядоченность системы, тем выше энтропия системы.
4) Энтропия - мера деградации энергии системы, ее превращения в теплоту, поскольку (согласно одному из постулатов Планка) любая форма энергии может полностью превратиться в теплоту, однако теплота превращается в другие формы энергии лишь частично. Энтропия — мера рассеяния теплоты по частям (или частицам) системы.
Цикл карно
Термодинамический цикл - это замкнутый процесс, совершаемый термодинамической системой, который можно многократно повторять.
Замкнутый (круговой) процесс — изменение состояния термодинамической системы, в результате которого система возвращается в первоначальное состояние. При этом изменение внутренней энергии равно нулю (∆U = 0), а теплообмен (теплота) Q равен внешней работе W. Если теплота Q и внешняя работа W положительны, то система совершает работу за счет полученной извне теплоты. Если теплота Q и внешняя работа отрицательны, то система отдает теплоту вследствие действия внешних сил.
Рассмотрение одного из замкнутых круговых процессов - так называемого цикла Карно — позволяет дать формулировку второго начала термодинамики и математически обосновать введение энтропии S для обратимых процессов как функции состояния системы, изменение которой равно приведенной теплоте процесса.
к |
|
2 |
|
||
|
||
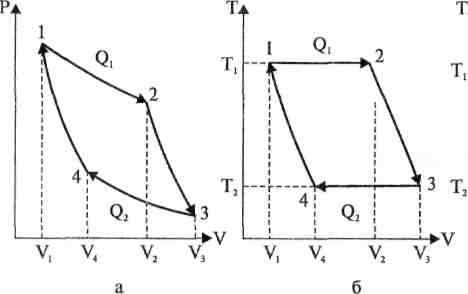
Рис. 1. Цикл Карно в разных координатах: давление Р — объем V, температура Т - объем V, температура Т - энтропия S.
Рис. 1. Цикл Карно в координатах Р — V (а), Т — V (б), Т — S (в) : 1—>2 — изотермическое расширение газа от объема V1 до объема V2 ; 2—>3 — адиабатическое расширение газа от объема V2 до объема V3; 3->4 - изотермическое сжатие газа от объема V3 до объема V4; 4—>1 — адиабатическое сжатие газа от объема V4 до объема V1,. Q1 — тепло, поступающая в «нагреватель», Q2 — тепло, возвращаемая «холодильнику» (Q2 < Q1).
Идеальная тепловая машина Карно содержит «нагреватель» при температуре Т1 и «холодильник» при более низкой температуре Т2. Рабочее тело - газ - последовательно вначале изотермически расширяется при температуре Т1 от объема V1 до объема V2, затем адиабатический расширяется от объема V2 до объема V3, после чего изотермически сжимается при температуре Т2 от объема V3 до объема V4 и, наконец, адиабатический сжимается от объема V4 до объема V1, возвращаясь в исходное положение 1.
Изотерма 1>2 соответствует изотермическому расширению газа от объема V1 до объема V2 с поглощением теплоты Q1 у «нагревателя». Адиабата 2->3 отвечает адиабатическому расширению газа от объема V2 до объема V3. Изотерма 3->4 отвечает изотермическому сжатию газа от объема V3 до объема V4; при этом газ возвращает теплоту Q2 (Q2<Q1) «холодильнику». Адиабата 4->1 соответствует адиабатическому сжатию газа от объема V4 до объема V3.
Разность Q1 - Q2 отвечает работе, которую при одном обратимом цикле совершила тепловая машина. Эта работа равна по рис. 1 площади цикла 1->2 3->4->1 в координатах P-V.
Коэффициент полезного действия η тепловой машины в цикле Карно равен Q1 - Q2 Т1 - Т2
η = -------------- = ----------------
Q 1 Т1
где Q1 и Q2 - соответственно теплота, полученная рабочим телом газом от «нагревателя» при температуре Т1 и теплота, частично возвращенная «холодильнику» при температуре Т2; Т2 < Т1 .
Таким образом, коэффициент полезного действия η идеальной тепловой машины зависит только от разности температур «нагревателя» и «холодильника» и не зависит от природы рабочего тела тепловой машины. Коэффициент полезного действия любой тепловой машины не может быть больше коэффициента полезного действия идеальной тепловой машины цикла Карно.
Лекция №4.2
