9. Лабораторная работа № 6 системы счисления и арифметические операции над числами

9.1. Цель работы

Научиться переводить числа из одной системы счисления в другую и выполнять простейшие арифметические операции над числами

9.2. Теоретическая часть

Система счисления - совокупность различных приемов обозначе­ния чисел., Если при записи числа одна и та же цифра имеет различ­ное значение (в зависимости от позиции), то система счисления называется позиционной в

Например: 7 7 7

- число единиц

- число десятков

-число сотен

В общем виде любое число в позиционной системе счисления имеет вид

а₁ а₂ а₃ … а_к-1 а_к = а₁Нt^-1 + а₂Нt^-2 + а₃Нt^-3 + … а_кНt^-к,

где Н - основание системы;

к - количество разрядов в числе;

• - фиксированное число равное числу разрядов до запятой.

Основание системы – это количество символов используемых для представления числа. Исторически сложилось так, что наибольшее распространение получила десятич­ная система счисления (на руках 10 пальцев).

Например: 359,78 = 3*10² + 5*10¹ + 9*10⁰ + 7*10^-1 + 8*10^-2

Н = 10; t = 3; к = 5.

Однако, в вычислительной технике применяют и другие системы счис­ления.

Шестнадцатеричная: на месте коэффициентов a_n, a_n-1, … a₁ могут быть любые из шестнадцати символов.

десятичные числа	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
шестнадцатеричные числа	0	1	2	3	4	5	6	7	8	9	А	В	С	D	Е	F

Основание Н такой системы является число 16.

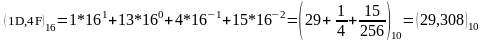
Восьмеричная: на месте коэффициентов a_n, a_n-1, … a₁ могут быть первые восемь цифр десятичного алфавита

0, 1, 3, 4, 5, 6, 7

Основанием Н такой системы является число 8

(213,4)₈ = 2*8² + 1*8¹ + 3*8⁰ + 4*8^-1 = (139,5)₁₀

Двоичная: используются всего две цифры 0 и 1

Основанием Н такой системы является число 2.

(10101)₂ = 1*2⁴ + 0*2³ + 1*2² + 0*2¹ + 1*2⁰ = 16 + 4 + 1 = (21)₁₀

Двоичная система получила наибольшее распространение в вычисли­тельных машинах из-за простоты схемной реализации устройств, т.к. в природе очень много явлений, имеющих два состояния (включено и выключено, намагничено - размагничено, транзистор открыт - транзистор закрыт, есть отверстие в перфокарте или его нет). Микропроцессор К580ВМ80А тоже работает с двоичными числами, однако вводят их в УМК устройство памяти в шестнадцатеричной системе счисления, т.к. такой ввод короче. Восьмеричная система счисления применяется при вводе чисел в персональных ЭВМ серии ДВК.

Для того, чтобы перевести целое число Х из одной системы счисления с основанием Н в новую систему счисления с основанием Н¹ необходимо последовательно делить заданное число и получающиеся в процессе деления частные на основание новой системы до тех пор, пока последнее частное не окажется меньше нового осно­вания. Результат перевода запишется в виде последовательности цифр, начиная с последнего частного и заканчивая первым остатком,

Например, перевести число 875 из десятичной системы в дво­ичную.

875	2
874	437	2
1	436	218	2
	1	218	109	2
		0	108	54	2
			1	54	27		2
				0	26		13		2
					1		12		6		2
							1		6		3		2
									0		2		1
(875)10 = (1101101011)2										1

Для того, чтобы перевести правильную дробь из системы с од­ним основанием в другую, нужно произвести последовательное умножение этой дроби и получающихся дробных частей произведений на основание новой системы. Результатом перевода является прямая последовательность целых частей полученных произведений. Если дробная часть не равна нулю, то производят округление. Например, перевести десятичную дробь 0,125 в двоичную систему счисления.

направление чтения	0	125	Х2
	0	250	Х (0,125)10 = (0, 001)2 2
	0	500	Х2
	1	000

Перевод чисел из двоичной системы в шестнадцатеричную производится по следующим правилам. Двоичное число разбивают на группы по 4 разряда, начиная с младшего. Если в старших разря­дах не хватает цифр до четырех знаков, то в качестве недостаю­щих цифр добавляют нули. Взамен этих групп по 4 разряда записывают числа в шестнадцатеричном коде.

Например, 1 1001 1010 = 0001 1001 1010

1010 = 1*2³ + 0*2² + 1*2¹ + 0*2⁰ = 8 + 2 = (10)₁₀ = А₁₆

1001 = 1*2³ + 0*2² + 0*2¹ + 1*2⁰ = (9)₁₀ = 9₁₆

0001 = 0*2³ + 0*2² + 0*2¹ + 1*2⁰ = (1)₁₀ = (1)₁₆

Таким образом, (1 1001 1010)₂ = (19А)₁₆

Проверку можно осуществить переводом чисел в десятичную систему счисления:

110011010 = 1*1⁸+1*2⁷+0*2⁶+0*2⁵+1*2⁴+1*2³+0*2²+1*2¹+0*2⁰ =

256 + 128 + 16 + 8 + 2 = (410)₁₀

(19А)₁₆ = 1*16²+9*16¹+10*16⁰ = 256 + 144 + 10 = (410)₁₀

Перевод чисел из двоичной системы в восьмеричную произво­дится по следующему правилу. Двоичное число разбивают на группы по 3 разряда (бита), начиная с младшего. Если в старших разрядах не хватает цифр до трех знаков, то в качестве недостающих цифр добавляют нули. Группы по три разряда переводят из двоичной системы в восьмеричную и записывают получившееся число.

Например, 110 011 010 = (632)₈

010 = 1*2¹ = 2

011 = 1*2¹ + 1*2⁰ = 3

110 = 1*2² + 1*2¹ = 6

При записи чисел в шестнадцатеричной системе счисления после самого числа ставится буква Н, обозначающая шестнадцатеричную систему, например, 8IH, ААН, А9Н, и т.д. При записи чисел в двоичной системе счисления после комбинации нулей и единиц, ставится буква В (binary - двоичный), например, 0101В. При запи­си чисел в десятичной системе счисления ставится буква D, например, 356 D).

Для удобства начинающих переводить числа из одной системы в другую приводится таблица переводов.

Таблица 1

СИСТЕМЫ СЧИСЛЕНИЯ
Десятичная	Двоичная	Восьмеричная	Шестнадцатеричная
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15	0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111	0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17	0 1 2 3 4 5 6 7 8 9 А В С D Е F