4.2. Математическая обработка данных

Термин данные относят ко всем символическим продуктам эксперимента. Снятые (записанные) непосредственно прибором или зарегистрированные визуально данные называются необрабо- танными и подлежат обработке — усреднению и оценке вариации значений.

При всех вычислениях с приближенными числами (а именно только приближенные числа получают в эксперименте) следует помнить:

1. Результаты измерений и вычислений должны содержать строго определенное число значащих цифр в соответствии с точностью метода, причем последняя цифра должна быть сомни- тельной, а предпоследняя достоверной.

2. Отбрасывая неточные цифры, надо пользоваться правилом округления.

3. Если в вычислениях используется какое-либо не очень надежное число, то точность конечного результата не может быть большей, чем точность наименее надежного числа в цепи вычислений. В результатах анализа древесины и цел- люлозы используют приближенные числа, обычно имеющие 3 значащие цифры.

4. При сложении и вычитании приближенных чисел нужно в конечном результате сохранять не больше знаков после запятой чем их имеется в наименее достоверном числе.

5. При умножении и делении результат следует округлять до такого числа значащих цифр, сколько их имеет приближен- ное число (значение) с наименьшим числом значащих цифр. Например: 16,342,1=34 (две значащие цифры).

6. В промежуточных результатах всех арифметических действий следует оставлять на одну цифру больше, чем это требуют правила 4 и 5 для конечного результата.

7. При возведении в степень или извлечении корня число значащих цифр сохраняется.

8. Точность измерений одной и той же величины (помещен- ной в одной графе таблицы) должна быть одинаковой, а раз- личных величин может быть различна и зависит от точности определения.

Среднее арифметическое значение , полученное по резуль- татам испытаний выборки, и среднее квадратическое отклонение

s являются приближенными оценками соответствующих пара- метров генеральной совокупности — математического ожидания  и дисперсии ².

Рассмотрим смысл и способы расчета и s. Среднее арифметическое значение выборки, т. е. ограниченного и равного n числа показателей образцов партии, которая рас- сматривается как генеральная совокупность всех значений показателей, определяют по формуле

Среднее квадратическое отклонение, квадрат которого называют выборочной дисперсией, или эмпирическим стандартом, характеризует рассеивание (вариацию) изучаемых случайных величин вокруг среднего значения. Формулы для расчета

или

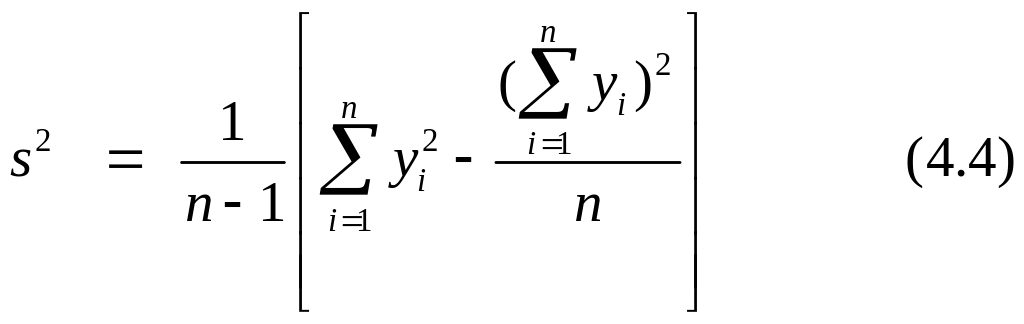
Вычисления по формулам (4.3) и (4.4) равноценны, но последняя обладает меньшей погрешностью округления, посколь- ку среднее арифметическое не вычисляется.

Кроме того, рассчитывают ошибку среднего арифме- тического m с учетом задаваемой доверительной вероятно- сти Р и числа параллельных определений n, используя для этой цели критерий Стьюдента (или t-критерий), зна- чения которого приведены в табл. 4.1, где f — число степеней свободы, равное n—1.

Доверительной вероятностью называют вероятность нахождения истинного значения параметра генеральной со- вокупности  в некоторых пределах. Эти пределы называют доверительными границами, а образуемый ими интервал — доверительным интервалом

f	P					f	P
	0,80	0,90	0,95	0,98	0,99		0,80	0,90	0,95	0,98	0,99
1	3,08	6,31	12,7	31,8	63,7	6	1,44	1,94	2,45	3,14	3,71
2	1,89	2,92	4,30	6,96	9,92	7	1,42	1,89	2,36	3,00	3,50
3	1,64	2,35	3,18	4,54	5,84	8	1,40	1,86	2,31	2,90	3,36
4	1,53	2,13	2,78	3,75	4,60	9	1,38	1,83	2,26	2,82	3,25
5	1,48	2,02	2,57	3,36	4,03	10	1,37	1,81	2,23	2,76	3,17

Тогда ошибка среднего арифметического

Обычно в научных исследованиях принимают Р в пределах от 0,9 до 0,95. Результат измерения записывают в виде: и n при P=0,95 (или 0,9). Иногда вместо доверительной вероятности указывают уровень значимости =1—P. Возможен второй способ записи, когда указывают только и n. В обоих случаях указание объема выборки n обязательно для возможного последующего сравнения данных.

Для оценки изменчивости измеряемых величин используют вариационный коэффициент v, %, или относи- тельное стандартное отклонение S_r

В качестве дополнительной характеристики выборок малого объема используют разность между крайними значениями ва- риационного ряда, которую называют размахом R.

При обработке данных необходима проверка наличия гру- бой ошибки, или «выскакивающего» значения у_. Проверку производят путем сравнения его с остальными ре- зультатами измерения. Рассчитывают величины и абсолют- ную разность между средним значением и «выскакивающим», выражают ее в долях s и сравнивают полученное значение t_P со значением критерия Стьюдента (см. табл. 4.1)

Этот расчет выполняют без учета y_. Если , то с надеж-

ностью вывода, соответствующего заданной доверительной вероятности Р, считают, что измерение у_, содержит грубую ошибку. Если t_P<t, то это само по себе еще не свидетель- ствует об отсутствии грубой ошибки. Можно говорить лишь об отсутствии оснований для исключения подозреваемого зна- чения. Таким же образом проверяют подозреваемое значение с другого конца вариационного ряда.

Для малой выборки среднее арифметическое существенно за- висит от значений крайних членов вариационного ряда, которые как раз и могут быть вызваны грубыми ошибками. Тогда для выявления «выскакивающего» значения используют Q-критерий, для чего рассчитывают

где y_n —«выскакивающее» значение; y_n-1 — значение резуль- тата, соседнего с y_n в вариационном ряду; R — размах выборки.

Если расчетное значение Q_P превосходит табличное Q (табл. 4.2), то результат y_n отклоняется и его следует исклю- чить. Также проверяют и при достаточности оснований исклю- чают другой крайний член ряда. Обоснованное решение исклю- чить одно заметно отклоняющееся значение из группы в три- четыре определения можно принять лишь после определения неслучайной причины ошибки. Для группы из пяти и более определений лучше исключить наибольшее и наименьшее зна- чение, чем какое-то одно. В целом нельзя исключать интуитивно сомнительный результат. Эксперимент необходимо повторить с тем, чтобы принять статистически обоснованное решение об исключении или сохранении результата. В противном случае лучше оставить сомнительное значение.

Если проводится серия точечных определений, то решение о достаточности определений принимается с учетом всех дан- ных, что обусловлено спецификой расчета и тем обстоятель- ством, что исследователь, как правило, стремится минимизи- ровать объем эксперимента. При этом решение принимают на основании оценки воспроизводимости.