2.2. Задачі, що потребують формалізації умови.

2.2.1. Прості задачі з одним розгалуженням.

1. Видрукувати у порядку зменшення значення двох чисел.

2. Видрукувати значення кореня квадратного з більшого з двох нерівних чисел.

3. Видрукувати в порядку збільшення значення двох нерівних чисел.

4. Автоматичний пристрій сортує деталі циліндричної форми з номінальним значенням діаметра D. Якщо деталь відповідає заданим вимогам, то на ній ставиться клеймо "Норма", якщо ні, – "Брак". Визначити клеймо деталі заданого діаметра.

5. Визначити, чи ввімкнено зовнішнє освітлення при відомій натуральній освітленості E люкс.

6. Відома довжина пробігу літака при посадці. Потрібно визначити, чи можлива посадка літака на аеродром з визначеною довжиною злітно-посадочної смуги.

7. У ВТК зважування деталей здійснюється на автоматичних терезах, настроєних на задану вагу. Якщо вага деталі відрізняється від заданої на величину, не більшу E, то потрібно видрукувати її вагу, в протилежному випадку – текст "Брак".

8. Визначити та видрукувати, чи можна перевезти трансформатор з відомою вагою на залізничній платформі заданої вантажопідйомності.

9. Обчислити значення функції y=sіn(x), використовуючи як аргумент менше з двох нерівних чисел.

10. Обчислити значення функції y=cos(3x), використовуючи як аргумент менше з двох нерівних чисел.

11. Обчислити значення функції y=sіn(0.5x²), використовуючи як аргумент менше з двох нерівних чисел.

12. Обчислити значення функції y=cos(3x+2), використовуючи як аргумент менше з двох нерівних чисел.

13. Обчислити значення функції y=e^-x+3.6, використовуючи як аргумент менше з двох нерівних чисел.

14. Обчислити значення функції y=x²+3x–4, використовуючи як аргумент менше з двох нерівних чисел.

15. Обчислити значення функції y=x³+2x–4, використовуючи як аргумент менше з двох нерівних чисел.

16. Обчислити значення функції y=x⁴+2x³–x²–1, використовуючи як аргумент менше з двох нерівних чисел.

17. Обчислити значення функції y=2sin²(x–0.8), використовуючи як аргумент менше з двох нерівних чисел.

18. Обчислити значення функції y=(x²+4)/(x–8), використовуючи як аргумент менше з двох нерівних чисел.

19. Обчислити значення функції y=3cos(2x), використовуючи як аргумент менше з двох нерівних чисел.

20. Обчислити значення функції y=(x²+2x–1)/(x+8), використовуючи як аргумент менше з двох нерівних чисел.

21. В'язкість розбавленої суспензії (за Ейнштейном) визначається емпіричним рівнянням _cc=_o(1+2.5c) при c < 0.05. Для великих концентрацій твердого c в суспензіях використовується формула _cc=_o(1+2.5c+7.349c²+16.2c³). За заданою концентрацією твердого c обчислити в'язкість розбавленої суспензії.

22. За заданою швидкістю руху рідини на похилій площині визначити, якою є течія (ламінарною чи турбулентною). Ламінарний рух визначається числом Рейнольдса Re<1000, Re=Vh/v. В іншому разі – рух турбулентний.

23. Б езпечне навантаження несучої колони S залежить від відношення її висоти h до діаметра d (R=h/d):

Обчислити безпечне навантаження несучої колони відомої висоти та діаметра.

24. Присвоїти модулю Юнга гірничих порід значення ₁=V²/1.21, якщо пористість ₀  2%, в протилежному випадку – ₂=V²/1.76.

25. При товщині зразка гірничої породи більшою або рівною 10 мм визначити швидкість подовжньої хвилі , в протилежному випадку – .

26. Обчислити значення характеристичного опору контура , якщо f  10 мГц , в іншому разі обчислення вести за формулою .

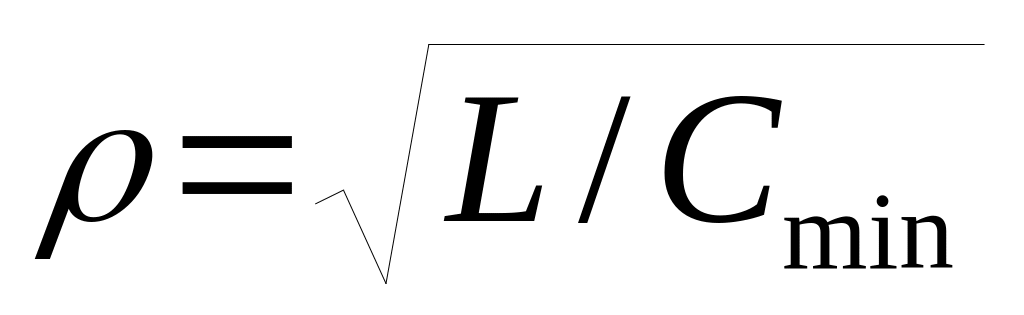27. Якщо значення функцій y₁=cos(3x) та y₂=sin(0.5x²) при одному значенні аргументу мають однакові знаки, видрукувати текст "Знаки однакові", в іншому разі видрукувати значення аргументу та функцій.

28. Якщо значення функцій y₁=sin(0.5x²) та y₂=tg(x)+2 при одному і тому ж значенні аргументу мають однакові знаки, то видрукувати текст "Знаки однакові", в протилежному випадку видрукувати значення аргументу та функцій.

29. Якщо значення функцій y₁=cos(3x+2) та y₂=e^-x при одному і тому ж значенні аргументу мають однакові знаки, то видрукувати текст "Знаки однакові", в протилежному випадку видрукувати значення аргументу та функцій.

30. Якщо значення функцій y₁=x²+3x та y₂=x²+8 при одному і тому ж значенні аргументу мають однакові знаки, то видрукувати текст "Знаки однакові", в протилежному випадку видрукувати значення аргументу та функцій.

31. Якщо значення функцій y₁=2sin(x)–0.8 та y₂=2sin(x–0.8) при одному и тому ж значенні аргументу мають однакові знаки, то видрукувати текст "Знаки однакові", в протилежному випадку видрукувати значення аргументу та функцій.

32. Якщо значення функцій y₁=x³+2x² та y₂=x²+4x при одному і тому ж значенні аргументу мають однакові знаки, то видрукувати текст "Знаки однакові", в протилежному випадку видрукувати значення аргументу та функцій.

33. Якщо значення функцій y₁=x³+8x та y₂=2x²+8 при одному і тому ж значенні аргументу мають однакові знаки, то видрукувати текст "Знаки однакові", в протилежному випадку видрукувати значення аргументу та функцій.

34. Якщо значення функцій y₁=x²+2x–1 та y₂=x–4 при одному і тому ж значенні аргументу мають однакові знаки, то видрукувати текст "Знаки однакові", в протилежному випадку видрукувати значення аргументу та функцій.

35. Якщо значення функцій y₁=2x²–3x+6 та y₂=3x–12 при одному і тому ж значенні аргументу мають однакові знаки, то видрукувати текст "Знаки однакові", в протилежному випадку видрукувати значення аргументу та функцій.

36. Якщо значення функцій y₁=tg(x) та y₂=tg(2x) при одному і тому ж значенні аргументу мають однакові знаки, то видрукувати текст "Знаки однакові", в протилежному випадку видрукувати значення аргументу та функцій.

37. Якщо значення функцій y₁=cos(3x) та y₂=cos(2x) при одному і тому ж значенні аргументу мають однакові знаки, то видрукувати текст "Знаки однакові", в протилежному випадку видрукувати значення аргументу та функцій.

38. Якщо значення функцій y₁=x²+sin(x) та y₂=x+cos(2x) при одному і тому ж значенні аргументу мають однакові знаки, то видрукувати текст "Знаки однакові", в протилежному випадку видрукувати значення аргументу та функцій.

39. Задана функція y=cos(3x). Якщо значення її додатне при відо-мому x, то видрукувати значення x, в протилежному випадку – величину цієї функції.

40. Задана функція y=sin(0.5x²). Якщо значення її додатне при відомому x, то видрукувати значення x, в протилежному випадку – величину цієї функції.

41. Задана функція y=tg(x)+2. Якщо значення її додатне при відомому x, то видрукувати значення x, в протилежному випадку – величину цієї функції.

42. Задана функція y=cos(3x+2). Якщо значення її додатне при відомому x, то видрукувати значення x, в протилежному випадку – величину цієї функції.

43. Задана функція y=e^-x+3.6. Якщо значення її додатне при відомому x, то видрукувати значення x, в протилежному випадку – величину цієї функції.

44. Задана функція y=x²+3x–4. Якщо значення її додатне при відомому x, то видрукувати значення x, в протилежному випадку – величину цієї функції.

45. Задана функція y=x³+2x–8. Якщо значення її додатне при відомому x, то видрукувати значення x, в протилежному випадку – величину цієї функції.

46. Задана функція y=x⁴+2x³–x²+1. Якщо значення її додатне при відомому x, то видрукувати значення x, в протилежному випадку – величину цієї функції.

47. Задана функція y=2sin²(x–0.8). Якщо значення її додатне при відомому x, то видрукувати значення x, в протилежному випадку – величину цієї функції.

48. Задана функція y=(x²+4)/(x–8). Якщо значення її додатне при відомому x, то видрукувати значення x, в протилежному випадку – величину цієї функції.

49. Задана функція y=3cos(2x). Якщо значення її додатне при відомому x, то видрукувати значення x, в протилежному випадку – величину цієї функції.

50. Задана функція y=(x²+2x–1)/(x+8). Якщо значення її додатне при відомому x, то видрукувати значення x, в протилежному випадку – величину цієї функції.

51. Обчислити значення функції y=e^x, взявши за аргумент більше з двох заданих чисел.

52. Електричний ланцюг, що складається з двох рівних за величиною опорів R, які можуть бути з'єднані послідовно (R_ek=2R) або паралельно (R_ek=R/2), підключається до джерела постійної напруги U. За відомою величиною струму I=U/R_ek у ланцюгу визначити, з'єднані ці опори послідовно чи паралельно.

53. Труба має внутрішній діаметр d. Зовнішній діаметр труби прий-няти рівним A , якщо у трубу можна вставити стержень прямокутного перерізу з розмірами B x C, в протилежному випадку зовнішній діаметр прийняти рівним E.

54. На однаковій відстані r у поле заряду q₀ почергово вносяться точечні позитивні заряди q₁ та q₂. За величиною сили , яка діє на заряди, визначити менший з них і, використовуючи його величину, обчислити напруженість поля E=F/q в точці на відстані r.

55. Коло з радіусом r і центром A(x₁, y₁) знаходиться усередині іншого кола з радіусом R і центром B(x₂, y₂). Якщо вони дотикаються, то визначити площі цих кіл, якщо ні – то r присвоїти значення нуль.

56. Вектор знаходиться у системі прямокутних координат XOY. За відомим значенням тангенсу кута, який утворений вектором з віссю абсцис, та значенням проекції вектора на вісь ординат, визначити, у якій напівплощині (праворуч чи ліворуч від вісі ординат) знаходиться вектор, присвоюючи змінній A значення "одиниця", якщо вектор знаходиться праворуч, і "нуль", якщо вектор знаходиться зліва від вісі ординат.

57. Якщо за трьома сторонами A, B, C (A має найбільшу довжину) можна побудувати трикутник, то обчислити його площу за формулою Герона , де p – напівпериметр трикутника, в протилежному випадку змінній S присвоїти зна-чення "0".

58. З а відсутністю балок прямокутного перерізу зі сторонами a та b, які використовуються при будівництві цеху, було вирішено замінити їх на балки круглого перерізу діаметром D. Видрукувати текст "Можна замінити", якщо площі поперечного перерізу балок однакові, в протилежному випадку обчислити максимальний прогин круглої балки за формулою .

59. Вектор OA заданий на площині XOY своїми проекціями OX і OY на координатні вісі. Визначити кут між ОХ і вектором ОА.

60. Заданий круг радіусу r. Задана площа іншого круга. Якщо перший круг уміщає другий або співпадає з ним, обчислити площу квадрата зі стороною a. В протилежному випадку видрукувати "Одиниця".

61. Задані круг з відомим радіусом та квадрат з відомою стороною. Якщо квадрат уміщається усередині круга (не виходить за його межі), видрукувати "Одиниця", в протилежному випадку – "Нуль".

62. Заданий квадрат з відомою стороною. Якщо його діагональ менша В, обчислити площу трикутника з основою z та висотою A. В протилежному випадку – площу трикутника з основою A та висотою B.

63. Якщо у прямокутний отвір з розмірами B x C (B>C) можна вставити трубу круглого перерізу з заданим зовнішнім діаметром, то внутрішній діаметр труби прийняти рівним E. В протилежному випадку обчислити площу поперечного перерізу круглого стержня з діаметром E.

64. Задані координати двох точок A і B. Визначити точку, яка розташована ближче до початку координат.

65. Видрукувати у порядку збільшення два числа, які є значеннями функцій tg(x) та ctg(x) від одного заданого аргументу.

66. Видрукувати у порядку збільшення два числа, які є значеннями функцій y₁=cos(3x) та y₂=sin(0.5x²) від одного аргументу x.

67. Видрукувати у порядку збільшення два числа, які є значеннями функцій y₁=sin(0.5x²) та y₂=tg(x)+2 від одного аргументу x.

68. Видрукувати у порядку збільшення два числа, які є значеннями функцій y₁=cos(3x+2) та y₂=e^-x від одного аргументу x.

69. Видрукувати у порядку збільшення два числа, які є значеннями функцій y₁=x²+3x та y₂=x²+8 від одного аргументу x.

70. Видрукувати у порядку збільшення два числа, які є значеннями функцій y₁=2sin(x)–0.8 та y₂=2sin(x–0.8) від одного аргументу x.

71. Видрукувати у порядку збільшення два числа, які є значеннями функцій y₁=x³+2x та y₂=x²+4x від одного аргументу x.

72. Видрукувати у порядку збільшення два числа, які є значеннями функцій y₁=x³+8x та y₂=2x²+8 від одного аргументу x.

73. Видрукувати у порядку збільшення два числа, які є значеннями функцій y₁=x²+2x–1 та y₂=3x–12 від одного аргументу x.

74. Видрукувати у порядку збільшення два числа, які є значеннями функцій y₁=2x²–3x+6 та y₂=3x–12 від одного аргументу x.

75. Видрукувати у порядку збільшення два числа, які є значеннями функцій y₁=tg(x) та y₂=tg(2x) від одного аргументу x.

76. Видрукувати у порядку збільшення два числа, які є значеннями функцій y₁=cos(3x) та y₂=cos(2x) від одного аргументу x.

77. Визначити час польоту літака в пункт B, якщо відомі відстань від аеродрому вильоту до пункту B, кількість та витрати палива і швидкість польоту. В випадку неможливості польоту видрукувати текст "Палива не досить" .

78. Сталевий зливок у прокатний стан попадає нагрітим до заданої температури. Зливок знаходиться в нагрівальному колодязі t сек. Визначити, чи придатний зливок для прокату, якщо температура його нагрівання залежить від часу T=A+B(1– e^t/C), де A, B, C – відомі коефіцієнти.

79. Визначити належність точки з заданими координатами внутрішній області круга, використовуючи нерівність (x – A)²+(y – B)² < R², де A і B – координати центру круга, R – радіус круга. Якщо так, то змінній E присвоїти значення 1, якщо ні – 0.

80. Магнетитовий концентрат очищується від кварцу у дешламаторі в залежності від швидкості падіння часток у воді. Якщо швидкість падіння частки не менша P , то ця частка "Магнетит", інакше – "Кварц". За відомим діаметром d і густиною  частки визначити та видрукувати значення швидкості і найменування мінералу. Швидкість падіння визначається за формулою , де q – прискорення сили ваги.

81. Якщо добуток двох цілих чисел знаходиться в інтервалі [a, b], видрукувати текст "Добуток у інтервалі", в протилежному випадку – "Добуток поза інтервалом".

82. Якщо поточна дата – перше січня 2005 року – видрукувати текст "Сьогодні Новий рік" , в протилежному випадку – "O'key".

83. Якщо поточний час між 12-00 та 13-00, видрукувати текст "Обідня перерва", в протилежному випадку – "Робота".

84. Якщо поточний час менший, чим 12-00, то видрукувати текст "Перша половина дня" , в протилежному випадку – "Друга половина дня".

85. Якщо поточна дата знаходиться між 1 липня 2005 року і 31 липня 2005 року, то видрукувати текст "Час відпустки", в протилежному випадку – "Час роботи".

86. Відоме показання вольтметра, який установлений в освітлювальній мережі. Якщо воно знаходиться у межах UU, видрукувати текст "Нормальна напруга", в протилежному випадку – "Відхилення більш можливого".

87. Якщо показання частотометра знаходяться в межах F  F, видрукувати текст "Стабільна робота", в протилежному випадку – "Вихід частоти за межі можливого".

88. Якщо виміряне значення сили струму більше, чим задане, видрукувати текст "Сильно", в протилежному випадку – "Слабо".

89. Якщо вага редуктора менша ніж вантажопід’ємність автомобіля, видрукувати текст "Можливе перевезення автотранспортом", в протилежному випадку – "Перевезення автотранспортом неможливе".

90. Якщо швидкість руху більша заданої, видрукувати текст "Перевищення швидкості", в протилежному випадку – значення фактичної швидкості.

91. Якщо число обертів двигуна менше заданого, видрукувати текст "Зниження обертів двигуна", в протилежному випадку – фактичне значення числа обертів двигуна.

92. Якщо швидкість вітру більша заданої величини, видрукувати текст "Вітряно", в протилежному випадку – "Тихо".

93. Якщо показання зовнішнього термометра вище заданої температури, то видрукувати текст "Спека", в протилежному випадку – значення фактичної температури.

94. Якщо показання зовнішнього термометра нижче заданої температури, то видрукувати текст "Сильний мороз", в протилежному випадку – значення фактичної температури.

95. Якщо показання барометра більше заданої величини, то видрукувати текст "Тиск зростає", в протилежному випадку – "Тиск падає".

96. Якщо фактична вологість повітря більше заданої, видрукувати текст "Волого", в протилежному випадку – "Сухо".

97. Якщо тиск у системі більше заданого, видрукувати текст "Аварійний тиск у системі", в протилежному випадку – "Нормальна робота".

98. Якщо висота вантажу більше заданої, видрукувати "Вантаж провезти під ЛЕП неможливо", в протилежному випадку видрукувати величину висоти вантажу.

99. Якщо термін зберігання виробу більше заданого, видрукувати текст "Непридатний", в протилежному випадку – "Придатний".

100. Якщо показання зовнішнього термометра нижче заданої температури, видрукувати текст "Ввімкнути опалення житлових будівель", в протилежному випадку видрукувати показання зовнішнього термометра.