Завдання 1 Завдання 2 Обчислити визначений інтеграл Обчислити визначений інтеграл
методом підстановки
1.∫(3x-2)²dx а=-2 b=3 ∫sinxdx/(1+cosx) а=0 b=π/2
2.∫(x²-1)²dx а=1 b=2 ∫√(x-7)dx а=8 b=7
3.∫(x+1)dx/√x а=0 b=4 ∫x²dx/(1-4x³) а=-1 b=0
4.∫(√x+1/√x+1)dx а=1 b=2 ∫x²dx/(1+x³) а=0 b=2
5.∫(x+2)²dx а=1 b=2 ∫sinxdx/(1-cosx)² а= π/2 b= π/2
6.∫(4-x)²dx а=2 b=3 ∫cosxdx/(2-sinx) а=π/6 b= π/2
7.∫(2+x)²dx а=1 b=4 ∫xdx/√(x²+144) а=-5 b=9
8.∫(3-2x)² а=0 b=1 ∫cosxdx/(³√(7sinx+1) а=0 b= π/2
9.∫(4-5x)²dx а=1 b=3 ∫(3+cosx)²*sinxdx а=0 b= π/2
10.∫(x+1)³dx а=0 b=1 ∫cosxdx/√sinx а= π/6 b= π/2
11.∫(2+3x)²dx а=2 b=3 ∫xdx/(x²-1)³ а=2 b=3
12.∫(4x+1)²dx а=1 b=4 ∫cosxdx/(2-sinx)² а=0 b= π/2
13.∫(5-3x)²dx а=2 b=3 ∫sinxdx/(3+cosx)³ а=0 b= π/2
14.∫(x-3)²dx а=1 b=3 ∫cos((π/3)-x)dx а= π/6 b= π/3
15.∫(x+2)²dx а=5 b=7 ∫x²dx/(x³+3)³ а=1 b=2
16.∫(4-x)²dx а=0 b=2 ∫dx/√(5x+1) а=0 b=3
17.(2x+5)²dx а=1 b=3 ∫x√(x²-7)dx а=2√2 b=4
18.(x-6)²dx а=1 b=3 ∫x√x²+1)dx а=0 b=√3
19.∫(x²+x+1)dx а=4 b=5 ∫sinxdx/(2cosx+3) а=0 b= π/2
20.∫(2-x²)²dx а=1 b=3 ∫dx/³√(7x+1)² а=0 b=1
21.∫(x²+3)²dx а=1 b=2 ∫x²dx/(x³+2)² а=1 b=2
22.∫(4-2x)²dx а=4 b=5 ∫√cosx*sinxdx а=0 b= π/2
23.∫(x²+3)²dx а=1 b=2 ∫sin2xdx а=0 b= π/2
24.∫(x+1)²dx а=0 b=1 ∫dx/(11+5x) а=-2 b=-1
25.∫(x-5)²dx а=2 b=4 ∫sinxdx/(1-cosx) а= π/2b= π/3
Індивідуальна робота №10
“Знаходження площі фігури за допомогою визначеного інтеграла”
Контрольні запитання для обов’язкового опрацювання:
1.Показати на малюнку площу, яку обчислюють за допомогою інтегралу ∫f(x)dx
S=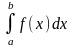
S=S1-S2,
де S1=
S2=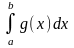
S=│ │
Індивідуальні завдання до практичного заняття №14:
“Знаходження площ фігур за допомогою визначеного інтеграла”
Завдання
Обчислити площу фігури, обмежену даними лініями і виконати побудову, якщо:
1.y=x2 і y=√x
2. y=1/3x3 і y=3x
3. y=4/x і y+x-5=0
4. y=8/x і y+x-9=0
5. y=x3 і y=2x
6. -2y+x+1=0, y+x-5=0 і y=0
7. x-y-5=0, y=0 і 2x-3y-6=0
8. y=6x-x2 -5 і y=0
9. y=2x-x2 і y=-x
10. y=x2 +4x і x-y+4=0
11.
y=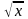
,
y=0 і
x=4
12. y=x2 і y=3-2x
13. y= x2 +1, y=0, x=0 і x=2
14. y=2 x2 +1 і y=x²+10
15. y= x2 і y=2-x²
16. y²=9x і x=4
17. y²=4 x, x=1 і x=9
18. y=1/3x3 ,y=0, x=-1 і x=2
19. y=-3 x2 y=0, x=1 і x=2
20. y=- x2 1, y=0, x=-2 і x=1
21. y= x2 -4 і y=0
22. x-2y-5=0, y=-2x і y=0
23. x-2y-6=0, y=-x і y=0
24. 2x+3y+6=0, y=0 і x=4
25. x-2y-6=0, y=0 , x=1 і x=5
Індивідуальна робота №11
“Розв’язування диференціальних рівнянь з відокремленими змінними та лінійних диференціальних рівнянь”
Контрольні запитання для обов’язкового опрацювання:
1.Визначення диференціального рівняння
2.Які існують розв’язки рівнянь?
3.Як визначають порядок диференціального рівняння?
4.Яке диференціальне рівняння називають диференціальним рівнянням з відокремлюваними змінними?
5.Що значить розв’язати задачу Коші?
Індивідуальні завдання до практичного заняття№15:
“ Розв’язування диференціальних рівнянь з відокремленими змінними та лінійних диференціальних рівнянь”
Знайти частинний розв’язок рівняння, якщо:
1.4xydx=(1+x²)dy, y(1)=1
2.y'=y/x , y(1)=5
3.y'=2+y, y(0)=3
4.xy'=2y, y(2)=3
5.(1+x)y'=y, y(0)=1
6.xdy=ydx, y(1)=2
7.2xydx=(1+x²)dy, y(1)=4
8.(1+x³)dy=x²ydx, y(0)=2
9.(2+x)dy=ydx, y(1)=3
10.dy=xydx, y(0)=2
11.(1+y)dy=(1+x)dx, y(0)=2
12.(x+3)dy=ydx, y(0)=6
13.ydy-xdx=0, y(2)=4
14.xdy=ydx, y(2)=6
15.dy=(3x²-2x)dx, y(2)=4
16.dy/dx=3x² , y(0)=6
17.dy/dx=4x+3, y(2)=15
18.y'=2x, y(2)=4
19.y'=3x², y(2)=8
20.y'=y/x, y(1)=9
21.y'=x+1, y(0)=2
22.y'=x-2, y(2)=10
23.dy/dx=6x², y(0)=4
24.y'=4x³, y(1)=1
25.dy-2xdx=0, y(1)=4