
- •Міністерство освіти і науки україни коледж електрифікації дніпропетровського державного аграрно-економічного університету
- •Методична розробка
- •Передмова
- •Індивідуальна робота №7
- •Знайти інтеграл безпосередньо : Знайти інтеграл методом підстановки :
- •8.∫(√X-(1-X)/X)dx ∫dx/xlnx
- •20.∫(Ax-1)dx ∫sinx*cos²xdx
- •Завдання 1 Завдання 2 Обчислити визначений інтеграл Обчислити визначений інтеграл
Міністерство освіти і науки україни коледж електрифікації дніпропетровського державного аграрно-економічного університету
ЗАТВЕРДЖУЮ
Заступник директора
з навчальної роботи
_________________ « » 2014р.
Методична розробка
М а т е р і а л и
для підготовки і проведення практичних занять з вищої математики у вищих навчальних закладах 1 та 2 рівнів акредитації, що здійснюють підготовку молодших спеціалістів на основі повної середньої освіти(2 курс)
Розробку розглянуто і схвалено предметною (цикловою) комісією
природничо-наукових дисциплін
Протокол № від _______________
Голова предметної (циклової) комісії
/ /
2014р.
Укладач: О.К.Гостєва, викладач коледжу електрифікації Дніпропетровського державного аграрно-економічного університету
Передмова
Підготовка студента до практичного заняття передбачає наявність конспекта з відповідями на запитання для обов’язкового опрацювання та виконання індивідуального завдання, яке він одержує на початку вивчення питань того чи іншого модуля. Номери індивідуального завдання відповідають порядковому номеру студента у журналі учбових занять
Оцінка студента залежить від якості відповідей на запитання для обов’язкового опрацювання, відповідей під час заняття та виконаного індивідуального завдання. Враховується і активність студента під час практичного заняття.
Подаємо фрагмент комплексу методичного забезпечення проведення практичних занять з вищої математики.
Індивідуальна робота №1
“Алгебраїчна форма комплексного числа. Дії над комплексними числами в алгебраїчній формі”
Контрольні запитання для обов’язкового опрацювання:
1. Як перемножуються два комплексних числа у алгебраїчній формі?
2. Як поділити два комплексних числа у алгебраїчній формі?
3. Як виглядає число в алгебраїчній формі
4. Що таке спряжені комплексні числа
5.Які дії виконують над комплексними числами в алгебраїчній формі?
6. Що таке уявна одиниця
7. Як комплексні числа позначаються на площині
8. Які комплексні числа називаються спряженими?
Індивідуальні завдання до практичного заняття №1 з теми:
“Алгебраїчна форма комплексного числа. Дії над комплексними числами”
Виконати додавання та віднімання комплексних чисел
1. z = 2 + 2j z = 2
2. z = -2 + 2j z = -2
3. z = 2 - 2j z = 3
4. z = -2 – 2j z = 4
z = 4 + 4j z = 5
z = 4 – 4j z = 6
z = - 4 + 4j z = 7
8. z = - 4 - 4j z = -3
9. z = 6 + 6j z = -4
10. z = 6 - 6j z = -5
11. z = - 6 + 6j z = -6
12. z = - 6 - 6j z = -7
13. z = 8 + 8j z = 15
14. z = 8 - 8j z = 10
15. z = -8 + 8j z = 9
16. z = -8 - 8j z = 8
17. z = 10 + 10j z = 11
18. z = 10 - 10j z = 12
19. z = -10 + 10j z = 13
20. z = -10 - 10j z = 14
21. z = 3 + 3j z = 20
22. z = 3 - 3j z = 19
23. z = -3 + 3j z = 18
24. z = -3 - 3j z = 16
25. z = -1 – j z = 17
26. z = -7 + 7j z = 1
Виконати множення та ділення
1. z1 = 2 + 2j z2 = 2+3j
2. z1 = -2 + 2j z = -2+3j
3. z1 = 2 - 2j z = 3-2j
4. z1 = -2 – 2j z = 4+3j
z1 = 4 + 4j z = 5-5j
z1 = 4 – 4j z = 6+3j
z1 = - 4 + 4j z = 7-j
8. z1 = - 4 - 4j z = -3+j
9. z1 = 6 + 6j z = -4+j
10. z1 = 6 - 6j z = -5+j
11. z1 = - 6 + 6j z = -6+j
12. z1 = - 6 - 6j z = -7+j
13. z1 = 8 + 8j z = 15-5j
14. z1 = 8 - 8j z = 10-3j
15. z1= -8 + 8j z = 9-j
16. z1 = -8 - 8j z = 8-2j
17. z1 = 10 + 10j z = 11-6j
18. z1 = 10 - 10j z = 12-j
19. z1 = -10 + 10j z = 13-j
20. z1 = -10 - 10j z = 14-j
21. z1 = 3 + 3j z = 20-j
22. z1 = 3 - 3j z = 19-j
23. z1 = -3 + 3j z = 18-3j
24. z1 = -3 - 3j z = 16-4j
25. z1 = -1 – j z = 17-5j
26. z1 = -7 + 7j z = 1+j
Індивідуальна робота №2
“Дії над комплексними числами у тригонометричній і показниковій формах”
Контрольні запитання для обов’язкового опрацювання:
1.Тригонометрична форма комплексного числа
2.Як визначають модуль та аргумент комплексного числа?
3.Як перемножаються два комплексних числа у тригонометричній формі?
4.Як поділити два комплексних числа у тригонометричній формі?
5.Піднесення до степеня комплексних чисел у тригонометричній формі
6.Добування кореня з комплексного числа у тригонометричній формі
7.Як перейти від тригонометричної форми комплексного числа до алгебраїчної?
8.Показникова форма комплексного числа
9.Які дії виконують над комплексними числами в показниковій формі ( перелічіть їх)?
10.Як перейти від алгебраїчної форми комплексного числа до показникової?
11.Як перейти від показникової форми комплексного числа до адгебраїчної?
12.Які дії не можна виконувати над комплексними числами у тригонометричній та показниковій формах?
13.Де застосовуються комплексні числа?
14.Яка з форм комплексних чисел є найбільш компактною?
Індивідуальні завдання до практичного заняття №2 з теми:
“Дії над комплексними числами у тригонометричній і показниковій формах”
Перейти до тригонометричної та показникової форм числа:
1. z = 2 + 2j z = 2
2. z = -2 + 2j z = -2
3. z = 2 - 2j z = 3
4. z = -2 – 2j z = 4
z = 4 + 4j z = 5
z = 4 – 4j z = 6
z = - 4 + 4j z = 7
8. z = - 4 - 4j z = -3
9. z = 6 + 6j z = -4
10. z = 6 - 6j z = -5
11. z = - 6 + 6j z = -6
12. z = - 6 - 6j z = -7
13. z = 8 + 8j z = 15
14. z = 8 - 8j z = 10
15. z = -8 + 8j z = 9
16. z = -8 - 8j z = 8
17. z = 10 + 10j z = 11
18. z = 10 - 10j z = 12
19. z = -10 + 10j z = 13
20. z = -10 - 10j z = 14
21. z = 3 + 3j z = 20
22. z = 3 - 3j z = 19
23. z = -3 + 3j z = 18
24. z = -3 - 3j z = 16
25. z = -1 – j z = 17
Індивідуальна робота №3
Тема« Обчислення визначників другого і третього порядку»
Контрольні запитання для обов’язкового опрацювання:
Що таке визначник другого порядку?
Що таке визначник третього порядку?
Властивості визначників
Індивідуальні завдання до практичного заняття 4:
Обчислити визначники
а)
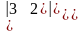 =,
б)
=,
б)
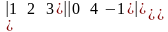 =
=а)
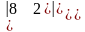 =,
б)
=,
б)
 =
=а)
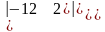 =,
б)
=,
б)
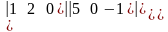 =
=а)
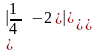 =,
б)
=,
б)
 =
=а)
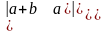 =,
б)
=,
б)
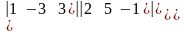 =
=а)
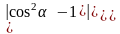 =,
б)
=,
б)
 =
=а)
 =,
б)
=
=,
б)
=а)
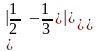 =,
б)
=,
б)
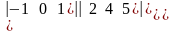 =
=а)
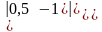 =,
б)
=,
б)
 =
=а)
 =,
б)
=,
б)
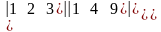 =
=а)
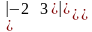 =,
б)
=,
б)
 =
=а)
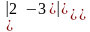 =,
б)
=,
б)
 =
=а)
 =,
б)
=,
б)
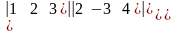 =
=а)
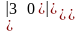 =,
б)
=,
б)
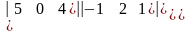 =
=а)
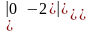 =,
б)
=,
б)
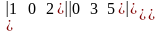 =
=а)
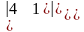 =,
б)
=,
б)
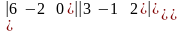 =
=а)
 =,
б)
=,
б)
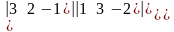 =
=а)
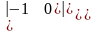 =,
б)
=,
б)
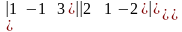 =
=а)
 =,
б)
=,
б)
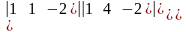 =
=а)
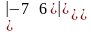 =,
б)
=,
б)
 =
=а)
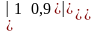 =,
б)
=,
б)
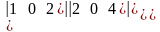 =
=а)
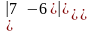 =,
б)
=,
б)
 =
=а)
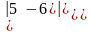 =,
б)
=,
б)
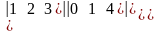 =
=а)
 =,
б)
=,
б)
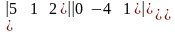 =
=а)
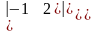 =,
б)
=,
б)
 =
=а)
 =,
б)
=,
б)
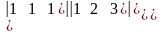 =
=а)
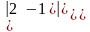 =,
б)
=,
б)
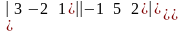 =
=а)
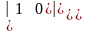 =,
б)
=,
б)
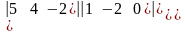 =
=а)
 =,
б)
=,
б)
 =
=а)
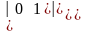 =,
б)
=,
б)
 =
=
Індивідуальна робота №4
“Розв’язування систем лінійних рівнянь”
Контрольні запитання для обов’язкового опрацювання:
Як розв’язати систему нерівностей ?
Які методи розв’язання систем рівнянь ви знаєте?
3. Метод Гауса розв’язування систем трьох лінійних рівнянь з трьома змінними
4. Метод Крамера розв’язування систем трьох лінійних рівнянь з трьома змінними
5. Що є розв’язком системи рівнянь?
6. Що є розв’язком системи нерівностей
Індивідуальні завдання до практичного заняття №5:
“Розв’язування систем лінійних рівнянь”
Завдання №1
Для визначення величини струмів у кожній із трьох віток електричного кола складено систему рівнянь:

– i1 + i2 – 3i3 = -7
2i1 + i2 – i3 = 0
3i1 – 2i2 + i3 = 5
Знайти величину струму i2 ?
Завдання №2
Для визначення величини струмів у кожній із трьох віток електричного кола складено систему рівнянь:

i1 – i2 – i3 = 0
i1 + i2 – 3i3 = 2
2i1 +3i2 – 5i3 = 7
Знайти величину струму i1 ?
Завдання №3
Для визначення величини струмів у кожній із трьох віток електричного кола складено систему рівнянь:

5i1 – 5i2 – 6i3= 1
–13i1 + 4i2 + 3i3 = 1
7i1 + i2 + i3 = 0
Знайти величину струму i1 ?
Завдання№4
Для визначення величини струмів у кожній із трьох віток електричного кола складено систему рівнянь:

i1 + i2 + i3= 6
3i1 – 2i2 – i3= 0
5i1 + 2i2 – 4i3 = 6
Знайти величину струму i3 ?
Завдання №5
Для визначення величини струмів у кожній із трьох віток електричного кола складено систему рівнянь:

i1 + 2i2 – i3= 7
2i1 – i2 + i3= 2
3i1 – 5i2 + 2i3 = -7
Знайти величину струму i2 ?
Завдання №6
Для визначення величини струмів у кожній із трьох віток електричного кола складено систему рівнянь:

2i1 + 3i2 – i3= 7
4i1 + 5i2 – 4i3= 3
3i1 – 3i2 + 2i3 = 2
Знайти величину струму i3 ?
Завдання №7
Визначити величину ємності с1 – одного із трьох паралельно з’єднаних конденсаторів, якщо їх взаємодія підпорядкована умовам:

с1 + с2 + с3= 8
с1 + с2 – 2с3= 1
3с1 – с2 – с3 = 4
Завдання №8
Визначити величину ємності с2 – одного із трьох паралельно з’єднаних конденсаторів, якщо їх взаємодія підпорядкована умовам:

7с1 + 3с2 +2с3= 21
7с1 – 4с2 + с3= 12
2с1 – 3с2 - с3 = –1
Завдання №9
Визначити величину ємності с2 – одного із трьох паралельно з’єднаних конденсаторів, якщо їх взаємодія підпорядкована умовам:

с1 + 2c2 + с3= 4
3с1—5с2 + 3с3= 1
2с1 + 7с2 – с3 = 8
Завдання №10
Визначити величину ємності с1 – одного із трьох паралельно з’єднаних конденсаторів, якщо їх взаємодія підпорядкована умовам:

2с1 + 3с2 – 4с3= -4
3с1 + 2с2 + 5с3=22
с1 – с2 + с3 = 2
Завдання №11
Визначити величину ємності с3 – одного із трьох паралельно з’єднаних конденсаторів, якщо їх взаємодія підпорядкована умовам:

с1 + с2 + с3= 6
с1 + 2с2 + 3с3= 10
2с1 + 3с2 – 4с3 = 8
Завдання№12
Визначити величину ємності с3 – одного із трьох паралельно з’єднаних конденсаторів, якщо їх взаємодія підпорядкована умовам:

3с1 + 4с2 – 3с3= 2
-3с1 + 4с2 + 3с3= 14
7с2 + 5с3 = 29
Завдання №13
Для визначення величини струмів у кожній із трьох віток електричного кола складено систему рівнянь:

i1 + i2 + i3= -2
i1 – i2 + 2i3= -7
2i1 + 3i2 – i3 = 1
Знайти величину струму i2 ?
Завдання №14
Для визначення величини струмів у кожній із трьох віток електричного кола складено систему рівнянь:

3i1 + i2 + i3= -2
5i1 – i2 – i3= 10
i1 – i2 + 5i3 = -12
Знайти величину струму i1 ?
Завдання №15
Для визначення величини струмів у кожній із трьох віток електричного кола складено систему рівнянь:

i1 + 2i2 + 3i3= 7
3i1 – 2i2 + 4i3= 11
2i1 + i2 – i3 = 0
Знайти величину струму i3 ?
Завдання №16
Для визначення величини струмів у кожній із трьох віток електричного кола складено систему рівнянь:
i1 – 2i2 + 2i3= 2
3і1 – 4i2 + i3= 3
5i1 + i2 – 3i3 = 8
Знайти величину струму i1 ?
Завдання №17
Для визначення величини струмів у кожній із трьох віток електричного кола складено систему рівнянь:

2i1 – i2 + 2i3= 3
i1 + 2i2 – i3= 0
3i1 – 2i2 + 2i3 = 2
Знайти величину струму i2 ?
Завдання №18
Для визначення величини струмів у кожній із трьох віток електричного кола складено систему рівнянь:

2i1 – i2 + i3= 1
i1 + 3i2 – 2i3= 3
3i1 – 2i2 + 4i3 = -1
Знайти величину струму i1 ?
Завдання №19
Для визначення величини струмів у кожній із трьох віток електричного кола складено систему рівнянь:

3i1 – 4i2 + 5i3= -3
2i1 + 3i2 – 2і3= 4
i1 – i2 + 3i3 = 1
Знайти величину струму i2 ?
Завдання №20
Визначити величину ємності с3 – одного із трьох паралельно з’єднаних конденсаторів, якщо їх взаємодія підпорядкована умовам:

с1 + 2с2 + с3= 8
3с1 + 2с2 + с3= 10
4с1 + 3с2 –2с3= 4
Завдання №21
Визначити величину ємності с3 – одного із трьох паралельно з’єднаних конденсаторів, якщо їх взаємодія підпорядкована умовам:

3с1 + 2с2 – 5с3= 0
2с1 – 3с2 + 4с3= 3
с1 + 2с2 –с3 = 2
Завдання №22
Визначити величину ємності с1 – одного із трьох паралельно з’єднаних конденсаторів, якщо їх взаємодія підпорядкована умовам:

с1 – с2 + 2с3= 5
3с1– 2с2 – с3= 1
4с1 + с2 +3с3= 10
Завдання №23
Визначити величину ємності с2 – одного із трьох паралельно з’єднаних конденсаторів, якщо їх взаємодія підпорядкована умовам:

2с1 – с2 + с3= 3
с1 + 2с2 – 2с3= -1
3с1 – 4с2 +с3 = 1
Завдання №24
Визначити величину ємності с3 – одного із трьох паралельно з’єднаних конденсаторів, якщо їх взаємодія підпорядкована умовам:

с1 – с2 + 2с3= 5
2с1 – 3с2 + с3= 3
3с1 + 2с2 – 2с3= 4
Завдання №25
Визначити величину ємності с1 – одного із трьох паралельно з’єднаних конденсаторів, якщо їх взаємодія підпорядкована умовам:

4с1 – 3с2 + 2с3= 0
2с1 + с2 – 3с3= 1
с1 – 2с2 +2с3= -1
Індивідуальна робота №5
“Дослідження функції на екстремум за допомогою першої похідної”
Контрольні запитання для обов’язкового опрацювання:
1.Середня швидкість зміни функції y=f(x) ∆y/∆x=(f(x+∆x)–f(x))/∆x
і що вона показує?
2.Миттєва швидкість зміни функції
3.Метод чотирьох кроків знаходження похідної функції
4.Визначення похідної функції y=f(x)
5.Фізичний сенс похідної
6.Геометричний сенс похідної
7.Визначення дотичної до кривої
8.Рівняння дотичної до кривої у данній її точці
9.Похідна функції y=x
10.Похідна функції y=c
11.Похідна функції y=√x
12.Похідна суми двох функцій y=u+v
13. Похідна добутку двох функцій y=uv
14.Похідна функції y=cx
15. Похідна частки двох функцій y=u/v
16.Похідна складеної функції
17.Правило знаходження екстремумів функції за допомогою першої похідної
Індивідуальні завдання до практичного заняття №7:
“Дослідження функції на екстремум за допомогою першої похідної”
Дослідити функцію на екстремум за допомогою першої похідної:
y=x²-4x
y=x²-x
y=x²+3x
y=-x²+2x
y=-x²-x
y=x²-8x+12
y=x²-4x+3
y=x²-10x+9
y=-x²+2x+3
y=-x²-x+6
y=-2x²+x+1
y=2x4-x
y=x³-3x²
y=1\3x³-x²
y=5-2√x²
y=33√x²-x
y=1/3x³-2x²-3x-4
y=-x4/4-x³-x²+7
y=x-12x²+9
y=1/3x³-x+1
y=1/3x³-9x
y=x²-8x+12
y=x²-6x+5
y=2x²-4x+5
y=-x²+4x+1
Індивідуальна робота №6
“Дослідження функції на екстремум за допомогою другої похідної”
Контрольні запитання для обов’язкового опрацювання:
1.Похідна функції y=sinu, де u=u(x)
2. Похідна функції y=cosu, де u=u(x)
3. Похідна функції y= tgu, де u=u(x)
4. Похідна функції y= ctgu, де u=u(x)
5. Похідна функції y=arcsinu, де u=u(x)
6. Похідна функції y=arccosu, де u=u(x)
7. Похідна функції y=arctgu, де u=u(x)
8. Похідна функції y=arcctgu, де u=u(x)
9.Теорема Лангранжа
10.Друга похідна функції y=f(x) (визначення)
11.Позначення другої похідної функції y=f(x)
12.Фізичний сенс другої похідної
13.Правило знаходження екстремумів функції y=f(x) за допомогою другої похідної
Індивідуальні завдання до практичного заняття 8
“Дослідження функції на екстремум за допомогою другої похідної”
Дослідити функцію на екстремум за допомогою другої похідної
1.y=x²–2x-3
2.y=2x²-3
3.y=x²–2x
4.y=-x²+4x
5.y=2x²–5x+2
6.y=-x²+x+6
7.y=x³-9x²+24x-12
8.y=1/3x ³-2x²+3x+4
9.y=1/3x³-3x²+5x+5
10.y=x³-9/2x²+6x-2
11.y=x4+3x²–2
12.y=x²–4x+3
13.y=x²–6x+13
14.y=8-1/2x²
15.y=1/2x²–1/3x³
16.y=6x²–x³
17.y=x³-3x²–9x+35
18.y=-x³+9x²–24x+10
19.y=x³
20.y=-x²–1
21.y=x²+3x-1
22.y=x³–x
23.y=1/3x³-3x²+8x-4
24.y=x²–4
25.y=3x-x³
