Решения

9 Класс

1. Мальвина и Буратино, поссорившись, пошли с равными скоростями в противоположные стороны. Через 13 минут Буратино решил помириться и, развернувшись, стал догонять Мальвину, увеличив скорость в 3 раза. Через сколько минут он догонит Мальвину?

Решение: Пусть Буратино за 13 минут прошел х метров и расстояние между ним и Мальвиной стало 2х метров. Тогда, догоняя, Буратино за 13 минут пройдет 3х метров (так как его скорость увеличилась в 3 раза), а за это время Мальвина пройдет х метров и они окажутся в одной точке.

Ответ: через 13 минут.

2. В футбольном турнире, в котором каждая из 8 участвующих команд сыграла с каждой по одному разу, команды набрали следующее число очков: 14, 12, 8, 8, 6, 4, 3, 1. Сколько очков команды, занявшие первые четыре места, потеряли в играх с остальными командами ( за выигранную игру команда получает 2 очка, за ничью - 1 очко, за проигрыш - 0 очков)? Ответ объясните.

Решение. Первые четыре команды сыграли с остальными 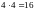матчей, а между собой 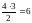матчей, и поэтому наибольшее число очков, которое они смогли набрать вместе, равно 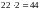. В действительности они набрали 42 очка и, следовательно, в играх с остальными командами они потеряли 2 очка.

3. Известно, что разность двух нечётных чисел делится на 5. На какую цифру оканчивается разность их кубов? (Напоминаем, что a³—b³=(a—b)(a²+ab+b²).)

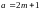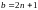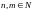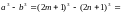
Решение. Пусть , , , тогда 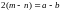- чётное число и делится на 5, следовательно, разность 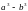оканчивается нулём.

4. Вера и Аня посещают математический кружок, в котором больше 91% мальчиков. Может ли в кружке быть меньше, чем 21 мальчик?

Решение.По условию две девочки составляют меньше 9% от числа участников кружка, так что 1% составляет больше ²/₉ человека, а 100% - больше ²⁰⁰/₉ человека, то есть не меньше 23 человек. Следовательно, мальчиков в этом кружке не может быть меньше, чем 21 человек.

МАТЕМАТИКА Школьный этап всероссийской олимпиады школьников 2014-2015

Решения

10 Класс

1. Назовем автобусный билет несчастливым, если сумма цифр его шестизначного номера делится на 13. Могут ли два идущих подряд билета оказаться несчастливыми?

Решение. Например, у идущих подряд чисел 444999 и 445000, сумма цифр равна 39 и 13 соответственно.

2. Для окраски одной грани кубика требуется 5с. За какое наименьшее время 3 человека могут выкрасить 188 кубиков (предполагается, что два человека не могут одновременно красить один кубик)?

Решение. Для покраски 188 кубиков потребуется всего 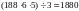(с) — наименьшее значение времени, которое отвечает условию задачи, если оно существует вообще (то есть нижняя граница). Докажем на примере, что нижняя граница существует.

Очевидно, что для того, чтобы затратить наименьшее количество времени, необходимо, чтобы каждый из трёх человек был занят работой от начала до конца. Для этого, например, сначала каждый человек полностью окрашивает по 61 кубику, а затем, в то время, когда двое окрашивают по кубику полностью, третий красит по две грани у трёх оставшихся кубиков, и, наконец, все трое красят по четыре грани у трёх кубиков. При этом они выполнят работу за 1880с.

Если же избрать другую организацию работы, например, пусть каждый будет красить все 6 граней кубика, тогда на окраске последних двух кубиков будут, естественно заняты только два человека и при этом потребуется 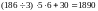(сек).

3. Известно, что длина любой из сторон треугольника меньше 1. Докажите, что его площадь меньше .

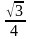Решение. Пусть в данном треугольнике АВС ВС – меньшая из сторон, тогда угол А не превышает 60°, т.е. sinА≤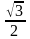 . Тогда S_∆АВС≤ ½АВВСsinA .

4. В учреждении стоит 14 канцелярских столов с одним, двумя, тремя и четырьмя ящиками. Всего в столах 33 ящика. Сколько столов с одним ящиком, если известно, что их столько же, сколько с двумя и тремя ящиками вместе?

Решение. Пусть x, y, z, v — число столов соответственно с одним, двумя, тремя и четырьмя ящиками. Тогда, исходя из условия, имеем систему:

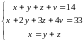
Из третьего и второго уравнений получаем, что 3y+4z+4v=33 или 4(z+v)=3(11—y). Тогда 11—y делится на 4, то есть y=7 или y=3.

В первом случае получаем 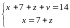, то есть 14+2z+v=14, 2z+v=0, что невозможно.

При y=3, решив систему, получим x=5.

Ответ: с одним ящиком было 5 столов.

МАТЕМАТИКА Школьный этап всероссийской олимпиады школьников 2014-2015