9 Методи наближення функцій

9.1 Поняття про наближення функцій

Часто при наукових дослідженнях виникають ситуації коли деяка функція відома тільки в певних точках, така функція може бути отримана експериментально або вона задана у вигляді таблиці. У таких випадках виникає задача наближення функції іншою функцією , яка є близькою до за певним критерієм узгодженості (наближення). Таку заміну однієї функції іншою називають апроксимацією або наближенням функцій. Аналітичний вираз функції , як правило, - невідомий.

Таким чином, задача наближення функції функцією полягає у побудові для заданої функції такої функції , що

. (9.1)

Як функцію наближення у (9.1) будемо використовувати многочлени або функції, які є лінійними по відношенню до своїх параметрів. У першому випадку говорять про поліноміальну апроксимацію або кусково-поліноміальну апроксимацію. У другому випадку лінійність параметрів функції дає змогу в явному вигляді отримати формулу, що визначає параметри функції, які залежать як від структури , так і від табличних значень функції . У залежності від вибору критерію наближення і від точок узгодження з (будемо називати їх вузлами), тобто точок, в яких відома інформація про функцію і, можливо, про її похідні, можна отримати різні способи апроксимації.

9.2 Наближення Лагранжа

Допускається, що в точках відомі точні значення як аргументу , так і самої функції . Нехай деяка крива, яка проходить через точки .

Якщо , наближення називають значенням інтерполяції^*. Якщо або , то називають значенням екстраполяції.

Інтерполяція – це процес побудови інтерполяційної функції. з метою знаходження проміжних значень табличної функції.

Нехай на відрізку в точках відомі значення функції .

Поставимо задачу знайти інтерполяційну функцію для , тобто таку функцію, значення якої в заданих точках (у вузлах інтерполяції) співпадають з табличними значеннями функції:

Будемо вважати, що функція є многочленом степеня .

Таким чином, нам необхідно розв’язати таку задачу: для табличної функції знайти многочлен степеня такий, що виконується сукупність умов інтерполяції

. (9.2)

Многочлен будемо шукати у такій формі:

. (9.3)

Оскільки степінь многочлена відомий, то розв’язок задачі інтерполяції зводиться до знаходження його коефіцієнтів: .

Найпростіший шлях розв’язку такої задачі – це скласти систему лінійних відносно коефіцієнтів рівнянь. Для цього як раз є умова (9.2). Таким чином, для того щоб многочлен (9.3) був інтерполяційним необхідно, щоб його коефіцієнти були розв’язком системи рівнянь

.

Практичне застосування цього методу є малоефективним. Тому для побудови інтерполяційного поліному користуються методом, який носить назву наближення Лагранжа.

Многочлен будемо шукати у такій формі:

.

Для того, щоб виконувались умови (9.2), функція в точці повинна дорівнювати одиниці і нулю в інших точках , тобто:

.

Рівність нулю многочлена в усіх вузлах інтерполяції, крім , означає, що можна записати у такому вигляді:

(9.5)

Коефіцієнт вводиться для того, щоб у точці виконувалась умова . Отже, для того щоб знайти значення , необхідно в (9.5) замість підставити його значення у вузлі інтерполяції і отриманий результат прирівняти до одиниці. У результаті отримаємо:

.

Звідси знаходимо:

.

Знаючи значення , знайдемо функцію . Для цього необхідно знайдене значення підставити у вираз (9.5)

.

Тепер можемо знайти інтерполяційний поліном Лагранжа шляхом підставлення функції у вираз (9.4)

. (9.6)

Оскільки поліноми Лагранжа використовуються для апроксимації (наближення) функції f(x), то поза вузлами інтерполяції . Тому важливо оцінити похибки, які при цьому виникають. Це можна зробити, використавши залишковий член ряду Тейлора, в якому множник слід замінити добутком

.

Це природно, оскільки інтерполяція здійснюється у кожному із вузлів , де . Отже, залишковий член ряду Тейлора для функції , який дає оцінку точності апроксимації, буде мати такий вигляд:

(9.7)

де - деяке значення із інтервалу [a;b]. Так як точка невідома, то у формулі (9.7) значення замінюють його верхньою оцінкою

.

Тоді

, (9.8)

де .

Формула (9.8) має практичне значення лише в тому випадку, коли відома функція , що в інженерній практиці трапляється рідко.

Приклад 9.1. Обчислимо ординати функції у рівновіддалених точках на відрізку . Візьмемо N=10 і відповідно , , а , де - початкова, - кінцева точки інтервалу [a; b] . Для значень аргументів функції обчислимо її ординати . Результати обчислень зведемо у таблицю 9.1.

Таблиця 9.1 - Ординати функції при вибраних

	0	0,5	1,0	1,5	2,0	2,5
	0	-0,08808	-0,052856	0,003954	0,086692	0,2138
	3,0		3,5	4,0	4,5	5,0
	0,3775		0,5453	0,6714	0,7137	0,6479

Отримані результати будемо вважати табличною функцією, для якої побудуємо інтерполяційний поліном Лагранжа. Для цього використаємо процедуру, яку назвемо PolynomialLagrange.

PolynomialLagrange

Наближення Лагранжа

Формування вхідних даних

Вхід:

N - кількість вузлів інтерполяції

x0 - початок інтервалу інтерполяції

xk - кінець інтервалу інтерполяції

Вихід:

Х - значення аргументу

У - значення функції f(x)

1 N=10

2 x0=0

3 xk=5

Обчислити значення функції f(x) у вузлах інтерполяції

Підпроцедура: Визначення коефіцієнтів Лагранжа

a - коефіцієнти полінома Лагранжа

Вхід: X - вектор абсцис

Y - вектор ординат

Вихід: а - матриця коефіцієнтів інтерполяції

полінома Лагранжа

d - матриця коефіцієнтів полінома Лагранжа розміром nxn

4 n=length(X) Кількість вузлів інтерполяції

5 N=n-1

6 Сформувати нульову матрицю a розміром nхn

Формування коефіцієнтів полінома Лагранжа

7 for k=1 to N+1

8 V=1;

9 for j=1 to N+1

10 if k~=j

11 then V=conv(V,poly(X(j)))/(X(k)-X(j))

12 end if

13 end for

14 =V

15 end for

Визначення коефіцієнтів інтерполяційного полінома Лагранжа

16 a=Y*d

Обчислення значень функції Р(х) у вузлах інтерполяції

16 N1=length(a)

17 for i=1 to Nn+1

18 S=0

19 for j=1 to N1

20 r=a(N1-j+1)*X1(i)^(j-1);

21 S=S+r

22 end for

23 P(i)=S

24 end for

Побудувати графіки функцій f(x) і P(x)

У процедурі PolynomialLagrange прийнято такі позначення: (рядок 14) - - тий рядок матриці ; poly – оператор, який створює вектор, компоненти якого коефіцієнти полінома з точно визначеними коренями ; conv – оператор, який утворює вектор компоненти якого – коефіцієнти полінома, який дорівнює добутку двох поліномів.

Після проведених розрахунків отримали такі значення коефіцієнтів інтерполяційного полінома Лагранжа: a₀=0; a₁= - 0,42814; a₂= 0,99119; a₃= - 0,89861; a₄= 0,47878; a₅ = - 0,1548; a₆= 0,033396; a₇= -0,0052074; a₈=0,58463·10^-3 a₉= - 0,41956·10^-6 a₁₀= 0,14143·10^-3

На рис. 9.1 показані графіки функцій і , а також „експериментальні” точки.

Видно, що значення їх ординат співпадають у вузлових точках з ”експериментальними” даними.

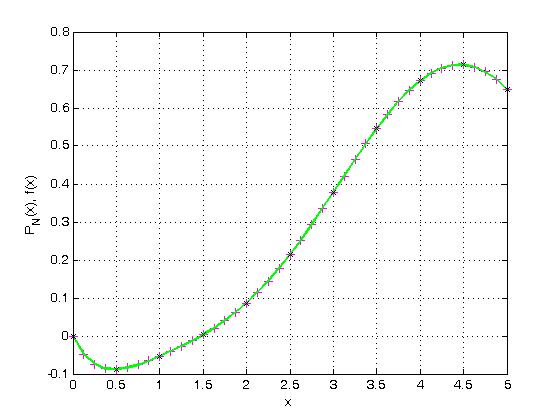
Рисунок 9.1 – Інтерполяція функції поліномом Лагранжа

Оскільки інтерполяція здійснюються для того, щоб знайти значення функції поза вузловими точками на проміжку [a;b], то, природно, поставити запитання про точність наближення Лагранжа. В даному випадку це можна зробити, так як відомо функція .

Обчислимо спочатку k-ту похідну від функції . Методом індукції^* можна показати, що

,

k=0,1,2,…

Далі знайдемо функцію , де - вузли інтерполяції і побудуємо графіки функцій і ( рис. 9.2).

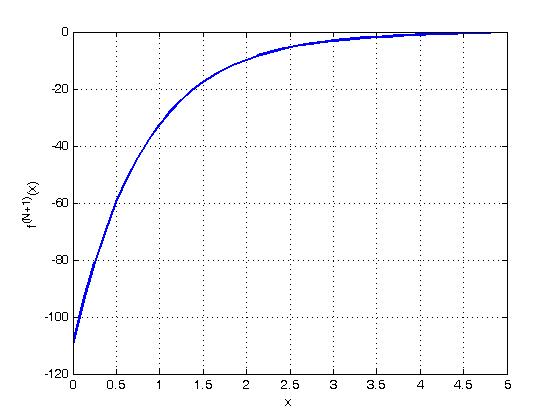
а)

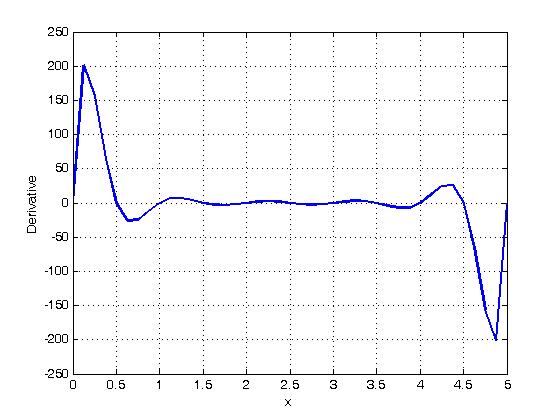
б)

Рисунок 9.2 – Графік функцій (а) і (б).

Із графіків функцій і знаходимо, що на відрізку [a=0;b=5] і . Підставляючи отримані значення і у формулу (9.8), знаходимо, що ,тобто в проміжних точках (поза вузлами інтерполяції) похибка наближена не перевершить величину 0,55248·10^-3.