Вопрос 2. Методы минимального риска

Методы минимального риска были развиты в связи с задачами радио­локации, но могут вполне успешно использоваться в задачах технической диагностики.

Пусть проводится измерение параметра (например, уровня вибраций изделия) и на основании данных измерений требуется сделать вывод о возможности продол­жения эксплуатации (диагноз – исправное состояние) или о направлении изде­лия в ремонт (диагноз – неисправное состояние).

На рис. 4 даны значения плотности вероятности диагностического параметра для двух состояний.

Рис. 4. Плотность вероятности диагностического признака

Пусть установлена контрольная норма для уровня вибрации . В соответствии с этой нормой принимают:

.

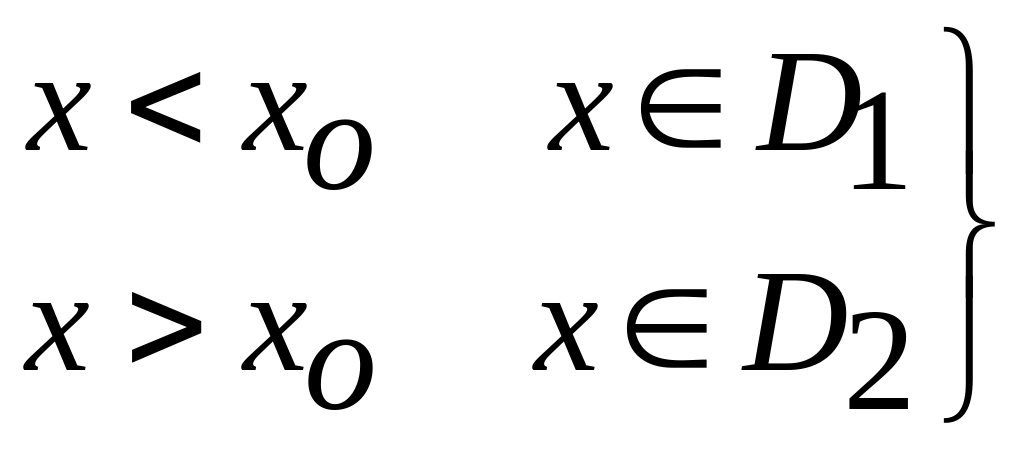Из рис. 4 следует, что любой выбор величины связан с определенным риском, так как кривые и пересекаются. Существуют два вида риска: риск «ложной тревоги», когда исправное изделие признают неисправным, и риск «пропуска цели», когда неисправное изделие считают годным.

В теории статистического контроля их называют риском поставщика и риском приемщика или ошибками первого и второго рода.

При вероятность ложной тревоги

,

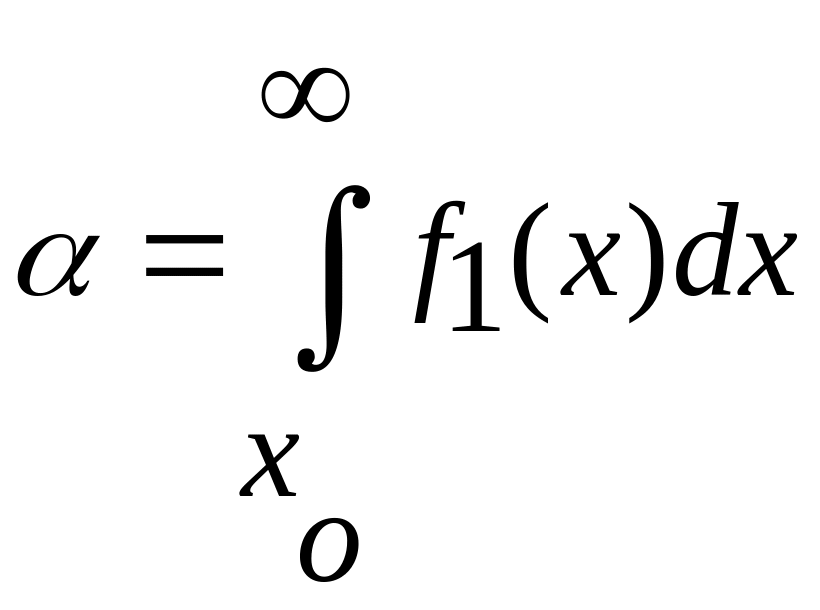вероятность пропуска цели

.

Задача теории статистических решений состоит в выборе оптимального значения .

По способу минимального риска рассматривается общая стоимость риска

,

где – «цена» ложной тревоги; – «цена» пропуска цели; и – априорные вероятности диагнозов (состояний), определяемые по предварительным статистическим данным. Величина R представляет собой «среднее значение» потери при ошибочном решении.

Из необходимого условия минимума

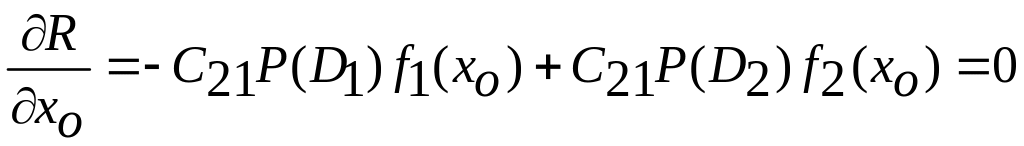
получаем

.

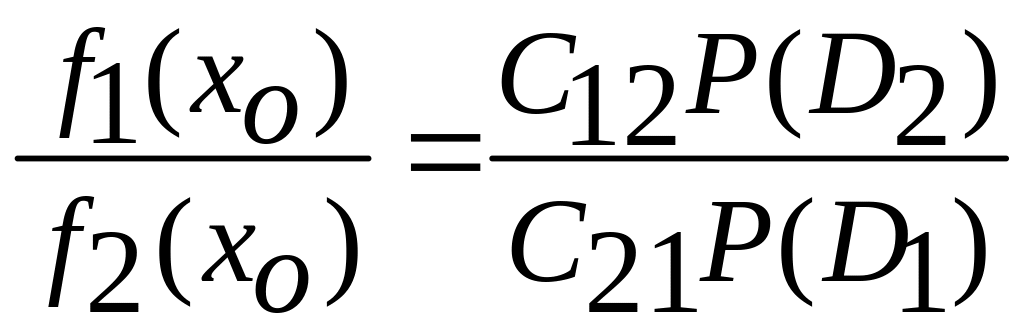Можно показать, что для одномодальных распределений данное условие всегда обеспечивает минимум величины R. Если стоимость ошибочных решений одинакова, то

.

Последнее соотношение минимизирует общее число ошибочных решений. Оно вытекает также из метода Байеса.

ЛИТЕРАТУРА

1. И.А.Биргер. Техническая диагностика. – М.: Машиностроение, 1978.

2. В.А. Пивоваров. Повреждаемость и диагностирование авиационных конструкций. – М.: Транспорт, 1994.

******************************************************************

Лекция 3. Метрические методы распознавания

Метрические методы связаны с измерением расстояний в пространстве признаков.

Будем характеризовать состояние системы (изделия) вектором параметров

.

Компоненты вектора могут быть непрерывными или дискретными вели­чинами. В последнем случае представляет собой (многоразрядный) диагностический признак.

Каждое состояние изделия, в соответствии с данным равенством, может быть представлено точкой в пространстве признаков, а вектор соединяет эту точку с началом координат. Предполагается, что точки с одним и тем же состоянием (диагнозом) группируются в компактной области пространства признаков («гипотеза компактности»).

Вопрос 1. Метод эталонов

Допустим, что имеется образцов с диагнозом (рис.5). Они образуют обучающую последовательность. Точки, входящие в области диагнозов, обычно располагаются более плотно в центральной части области.

Примем в качестве «типичного» изделия с данным диагнозом «среднюю точку», которую назовем эталоном.

Координаты эталона -го диагноза

( ),

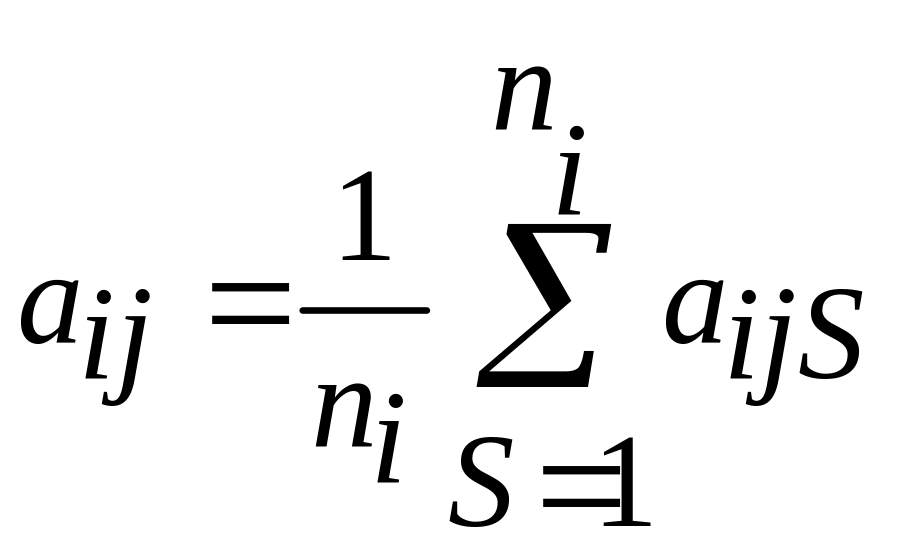где – значение параметра для образца , принадлежащего диагнозу .

Рис. 5. Область диагнозов (состояний) в пространстве признаков

Пусть предъявлено для распознавания изделие, характеризующееся вектором в пространстве признаков. Решение вопроса об отнесении изделия к диагнозу связано с измерением расстояния до эталонов.

Решающее правило принимается по минимальному расстоянию до эталона:

, ,

т, е. если точка ближе всего к эталону диагноза , то вывод делается в пользу диагноза .

Расстояния до i-го эталона

.

Предыдущие равенства определяют обычное евклидово расстояние.

В задачах диагностики часто оказывается целесообразным использовать обобщенные расстояния порядка .

.

При v=1 получается расстояние по Хемингу, при v = 2 – обычное расстояние. При возрастании v увеличивается роль наибольшего отклонения по какой-либо координате.

Расстояние можно использовать для однородного, изотропного прост­ранства признаков. Таким пространством будет пространство простых (двухразрядных) признаков, кодируемых двоичными числами (0,1).

Однако в задачах технической диагностики часто приходится использовать признаки различной физической природы (например, уровень вибрационных перегрузок и повышение температуры), имеющие различную размерность.

Для учета указанного обстоятельства целесообразно ввести безразмерные расстояния. Например, по координате (направлению) для точек и безразмерное расстояние можно принять в виде

,

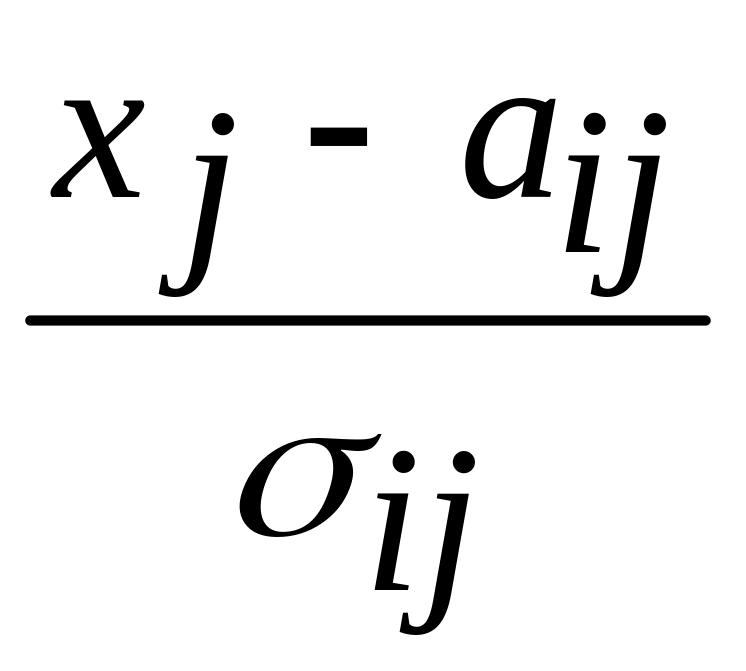где – среднее квадратическое отклонение признака для диагноза .

Условие содержит предположение, что для диагностики отклонение следует относить к «характерному масштабу» – среднему квадратическому отклонению.

Далее следует учесть различную диагностическую ценность признаков.

Для этого введем безразмерные диагностические коэффициенты и тогда получим

.

Последние соотношения дают формулы для расстоянии в неоднородном, неизотропном пространстве.

Определение коэффициентов вызывает известные трудности. В тех случаях, когда отсутствуют статистические сведения, величины можно назначать с помощью экспертных оценок или подбирать по опыту диагностики.