Теоретические основы технической диагностики

Одной из важных особенностей технической диагностики является распознавание состояния в условиях ограниченной информации, когда требуется руководствоваться определенными приемами и правилами для принятия решения.

Состояние системы описывается совокупностью (множеством) определяющих ее параметров (признаков). Множество определяющих параметров (признаков) может быть различным для разных задач распознавания.

Распознавание – процесс установления диагноза – состоит в отнесении предъявленной совокупности признаков к одному из типичных состояний. Число таких состояний зависит от особенностей задачи и целей распознавания. Часто требуется провести выбор одного из двух возможных состояний, например «исправное состояние» и «неисправное состояние». В других случаях необ­ходимо конкретизировать неисправные состояния: «разрушение подшипника», «разрушение шлицевого сообщения» и т. п.

Теория распознавания тесно связана с проблемой распознавания образов, изучаемой в кибернетике.

Постановка задачи технической диагностики состоит в следующем.

Имеется техническая система, которая может находиться в одном из таких состояний (диагнозов). Известна совокупность признаков (параметров), характеризующих каждое состояние системы. Требуется построить решающее правило, с помощью которого предъявленный для распознавания объект (набор признаков) был бы отнесен к одному из диагнозов.

Имеется несколько основных методов решения задач распознавания:

• вероятностно-статистические;

• метрические;

• логические;

• разделения в пространстве признаков.

Лекция 2. Вероятностно-статистические методы распознавания Вопрос 1. Метод Байеса

Основное преимущество статистических методов распознавания состоит в возможности одновременного учета признаков различной физической природы, так как они характеризуются безразмерными величинами – вероятностями их появления при различных состояниях системы.

Среди методов технической диагностики метод, основанный на обобщенной формуле Байеса, занимает особое место благо­даря простоте и эффективности.

Разумеется, метод Байеса имеет недостатки: большой объем предварительной информации, «угнетение» редко встречающихся диагнозов и др. Однако в случаях, когда объем статистических данных позволяет применить метод Байеса, его целесообразно использовать как один из наиболее надежных и эффективных методов.

Метод, основанный на обобщенной формуле Байеса, позволяет достаточно просто одновременно учесть признаки различной физической природы – дискретные и непрерывные. Это достигается благодаря использованию единообразных и безразмерных характеристик признаков – частот встречаемости (вероятностей) признаков при различных состояниях.

Если имеется диагноз и простой признак , то вероятность совместного появления событий (наличие у объекта состояния и признака )

.

Из последнего соотношения получаем

,

где в последнем равенстве – вероятность диагноза после того, как стало известно наличие у рассматриваемого объекта признака (апостериорная вероятность диагноза); – вероятность диагноза , определяемая по статистическим данным (априорная вероятность диагноза). Если обследовано объектов и состояние наблюдается в изделиях, то

,

где – вероятность появления объектов с состоянием . Если среди объектов с диагнозом у появился признак , то

,

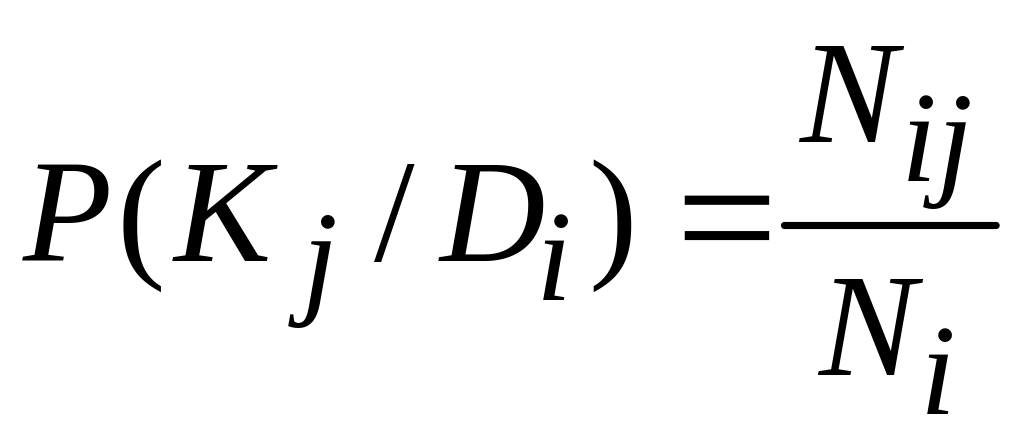– вероятность появления признака во всех объектах независимо от его состояния (диагноза). Пусть из общего числа признак обнаружен у объектов (с различным диагнозом). Тогда

.

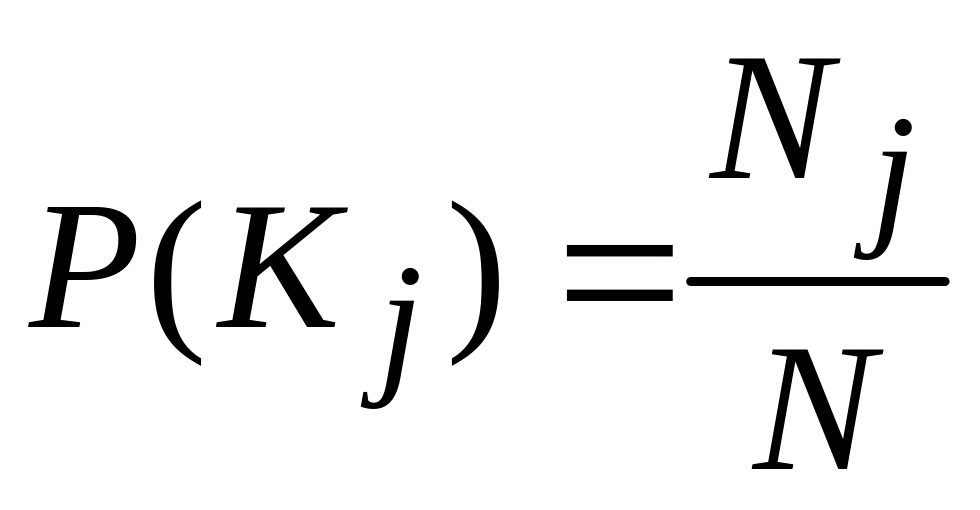Как будет ясно из дальнейшего, специальное вычисление не требуется.

Пусть проводится обследование ряда признаков по многоразрядным признакам и означает определенную реализацию комплекса признаков. При этом в каждом из признаков проявляется один из разрядов, например в приз­наке разряд :

.

Обобщенная формула Байеса (для комплекса многоразрядных признаков) имеет вид

.

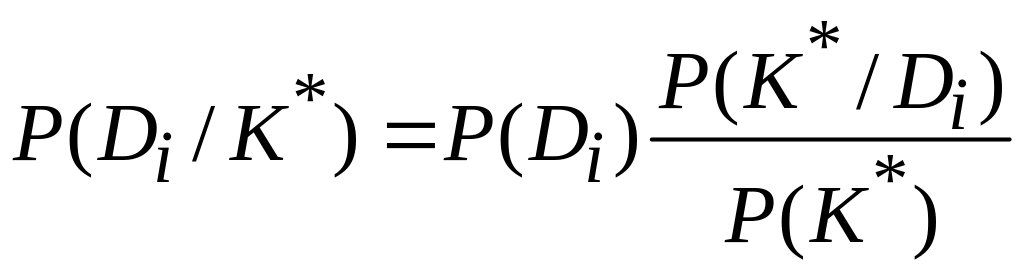
В последнем равенстве – вероятность диагноза , если комплекс признаков получил реализацию .

Для независимых и зависимых признаков формула Байеса будет несколько отличаться. В большинстве практических задач, особенно при большом числе признаков, можно принимать условие независимости признаков при наличии существенных корреляционных связей.

Предъявленный для распознавания объект, обла­дающий комплексом признаков , считают принадлежащем диагнозу , если

,

т. е. вероятность диагноза оказалась наибольшей.

Сумма вероятностей всех диагнозов

.

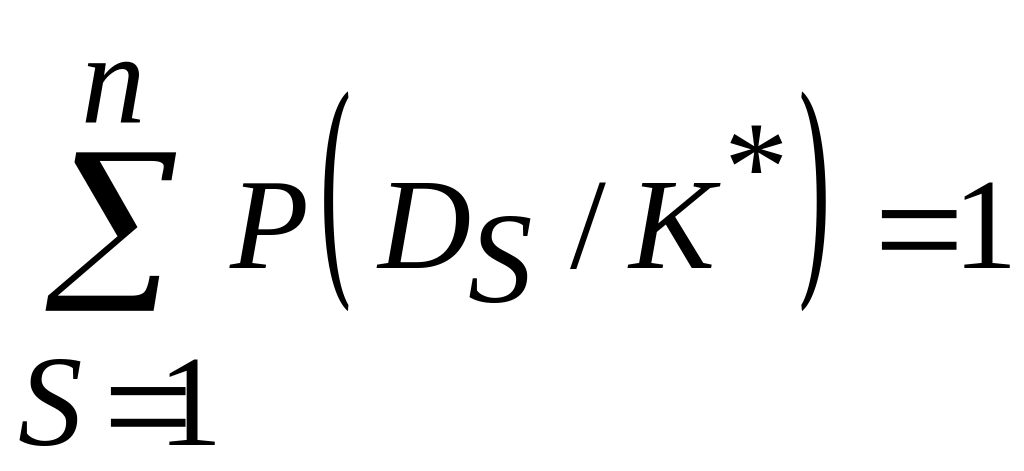Однако если вероятность не слишком велика (например, меньше 0,4 – 0,5), то следует отказаться от постановки диагноза. Поэтому решающее правило можно сформулировать следующим образом:

если ,

,

где – пороговое значение для диагноза (обычно принимают ).