Выч. методы Лаб. 4

Лабораторная работа №4

Численное решение задачи Коши для обыкновенных дифференциальных уравнений. Численное решение краевой задачи для линейного дифференциального уравнения 2-ого порядка. Решение дифференциальных уравнений в частных производных

Решение дифференциальных уравнений широко применяется в практике научно-технических расчетов. Это связано с тем, что дифференциальные уравнения (и системы из них) описывают поведение различных объектов в динамике, например переходные процессы в электронных схемах или работу часового маятника.

Для решения дифференциальных уравнений разработано значительное число аналитических и численных методов. В наиболее простых случаях, например если удается разделить переменные, решение находится простым интегрированием. Однако в большинстве случаев (особенно в прикладных задачах) найти точное решение бывает достаточно сложно. Поэтому такое распространение получили различные численные методы решения.

Обычно решение заключается в нахождении ряда значений x_i и y_i искомой зависимости y(x) при i, изменяющемся от 0 до N при шаге изменения x, равном h. До начала вычислений должны быть заданы начальные условия x₀ и y₀, шаг h, число итераций N.

Пусть необходимо найти решение уравнения

(1)

с начальным условием . Такая задача называется задачей Коши. Разложим искомую функцию в ряд вблизи точки и ограничимся первыми двумя членами разложения . Учтя уравнение (1) и обозначив , получаем Эту формулу можно применять многократно, находя значения функции во все новых и новых точках.

(2)

Такой метод решения обыкновенных дифференциальных уравнений называется методом Эйлера. Геометрически метод Эйлера означает, что на каждом шаге мы аппроксимируем решение (интегральную кривую) отрезком касательной, проведенной к графику решения в начале интервала. Точность метода невелика и имеет порядок h. Говорят, что метод Эйлера – метод первого порядка, то есть его точность растет линейно с уменьшением шага h.

Оценку значения производной можно улучшить, увеличивая число вспомогательных шагов. На практике наиболее распространенным методом решения обыкновенных дифференциальных уравнений является метод Рунге-Кутты четвертого порядка. Для оценки значения производной в этом методе используется четыре вспомогательных шага. Формулы метода Рунге-Кутты следующие

Перечисленные методы можно применять и для решения систем дифференциальных уравнений. Поскольку многие дифференциальные уравнения высших порядков могут быть сведены заменой переменных к системе дифференциальных уравнений первого порядка, рассмотренные методы могут быть использованы и для решения дифференциальных уравнений порядка выше первого.

Еще один тип задач, часто встречающихся на практике, – краевые задачи. Пусть имеется дифференциальное уравнение второго порядка . Решение уравнения требуется найти на интервале , причем известно, что Понятно, что произвольный интервал заменой переменных может быть сведен к единичному. Для решения краевой задачи обычно применяют метод стрельб. Пусть где k – некоторый параметр. Для некоторого пробного значения k может быть решена задача Коши, например, методом Рунге-Кутты. Полученное решение будет зависеть от значения параметра . Мы хотим найти такое значение параметра, чтобы выполнялось условие . Фактически мы свели исходную задачу к задаче решения трансцендентного уравнения с таблично заданной функцией. Если найдены такие значения параметра k₁ и k₂, что , то дальнейшее уточнение значения параметра можно проводить методом деления отрезка пополам.

Задание 1

Решить уравнение dy/dx=xy методом Эйлера Начальные значения x₀=0 и y₀=1. Вывести графическое представление точного и численного решения на общем графике.

Порядок выполнения задания

1. Присвоить переменной ORIGIN значение 1.

2. Задать величину шага h:=0.1;

3. Задать кол-во итераций N:=10 и порядок изменения индекса i;

4. Задать ф-цию f(x,y):=x y;

5. Задать начальные значения x₀ , y₀;

6. Ввести итерационные формулы ;

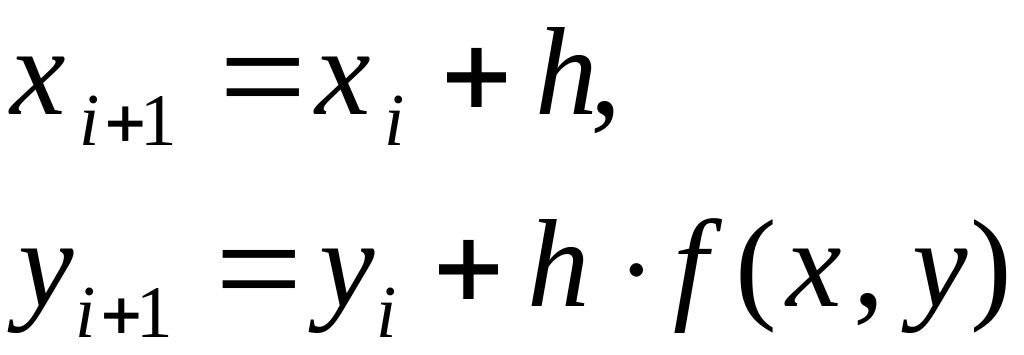7. Вывести значениия x_i , y_i;

8. Вывести график y_i(x_i);

9. Решить уравнение аналитически, разделив переменные.

Сравнить точное и численное решение на графике, найти относительную ошибку в точке x=1.

Задание 2.

Решить методом Рунге–Кутты на отрезке [0, ] задачу Коши для уравнения

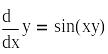, y(0)=1. Сравнить с решение, полученным с помощью функции rkfixe. Вывести график решения.

Порядок выполнения задания

1. Задать начальное значение;

2. Задать функцию D(x,y);

3. Присвоить матрице Y значение функции rkfixed на соответствующем отрезке.

4. Построить график (по оси абсцисс значения первого столбца матрицы Y, по оси ординат – второго).

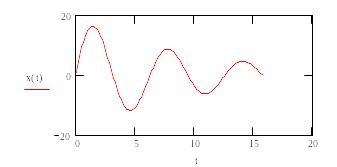
Задание 3.

Найти на отрезке [0, 3] приближенное решение задачи Коши:

y₁'= -y₂ +sin(xy₃), y₁(0)=1

y₂'= -y₁² , y₂(0)=0

y₃'= -y₃ - y₁, y₃(0)=1

и построить графики решения.

Порядок выполнения задания

1. Присвоить переменной ORIGIN значение 1.

2. Задать вектор начальных значений;

3. Задать вектор функцию D(x,y).

4. Присвоить матрице Y значение функции rkfixed на соответствующем отрезке.

5. Построить графики (по оси абсцисс значения первого столбца матрицы Y, по оси ординат – второго, третьего и четвертого).

Для решения дифференциальных уравнений MATHCAD имеет целый ряд встроенных функций. Функция rkfixed, предназначена для решения нормальных систем обыкновенных линейных дифференциальных уравнений. Решение в данном случае осуществляется методом Рунге- Кутты с постоянным шагом. Формат функции rkfixed(y, x1,x2,npoints,D), где y - вектор начальных условий, x1,x2 - начальная и конечная точка интегрирования, npoints - число узлов на отрезке [x1,x2], D - имя вектора-функции, содержащей правые части уравнения. При решении задачи Коши для уравнения первого порядка вектор решения имеет единственную компоненту y. Вектор правых частей содержит также одну компоненту. В первом столбце матрицы решения находятся координаты узлов равномерной сетки. Во-втором - приближенные значения решения в этих узлах.

Для решения обыкновенных дифференциальных уравнений можно использовать также блок given совместно с функцией odesolve. Дифференциальное уравнение совместно с начальными или граничными условиями записывается в блоке given. Производные можно обозначать как штрихами (Ctrl+F7), так и с помощью знака производной . Пример использования функции для решения задачи Коши приведен ниже.

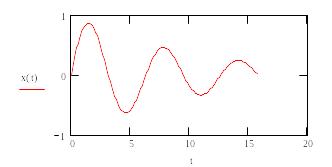
_{Обратите внимание! У искомой функции явно указан аргумент, знак производной стоит перед скобкой.}

_{Функция odesolve имеет три аргумента. Первый аргумент – независимая переменная, вторая – граница интервала, на котором ищется решение, последний аргумент – шаг, с которым ищется решение. Последний аргумент может быть опущен.}

_{Следующий пример демонстрирует решение краевой задачи. Использован другой способ записи производных, используется odesolve функция с двумя аргументами.}