Відображення і потужність Відображення. Відповідність. Функції.

Означення відображення

Нехай є дві множини і . Відображенням із множини в множину називається закон чи правило, за яким кожному елементу ставиться у відповідність цілком визначений єдиний елемент . Математично це записують так

.

Множина називається областю визначення відображення, а – областю значень відображення . Елемент називають образом (значенням) елемента при відображенні , це виражають також так: . Елемент називають прообразом (аргументом) елемента . Взагалі, якщо існує така підмножина , що для всіх елементів існують їх образи , то множина цих образів називається образом підмножини при відображенні , а множина називається прообразом підмножини . Підкреслимо, що при відображенні кожний елемент має тільки один образ: .

Таке означення відображення є дуже спорідненим з означенням функції . Часто ці означення не розрізняються. Але частіше функцією вважають таке відображення, яке є взаємно однозначним.

Крім відображення множини на (чи в) множину може існувати також відповідність елементів множин. Якщо певному елементу відповідає не обов’язково один елемент , то тоді говорять про відповідність. Це той випадок, коли для одного елемента існує декілька образів у множині . За такою відповідністю побудовані, наприклад, всі словники, у них завжди значенню слова в одній мові може відповідати декілька синонімів іншої мови.

Типи відображень.

Отже, при відображенні кожному елементу має відповідати єдиний елемент . Але зовсім не обов’язково, щоб кожний елемент був образом деякого елемента . Графічно це можна зобразити рис.1. На ньому є елементи (зовні круга) множини , які не є образами елементів множини . В цьому випадку не можна говорити, що множина відображається на множину , вона може відображатися лише в множину _.

Якщо ж будь-який елемент є образом принаймні одного елемента (а, можливо, і декількох), то таке відображення називається сюр’єктивним і при цьому говорять, що множина відображається на множину (відбувається накладання областей). Це означає, що для будь – якого елемента y Y існує прообраз . Сюр’єктивне відображення схематично можна зобразити рис.2.

Якщо для двох різних елементів їх образи і також різні, то відображення називається ін’єктивним.

При цьому теж може бути ситуація, коли не для кожного елемента є відповідний прообраз у множині .

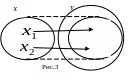
Відображення, яке одночасно є сюр’єктивним і ін’єктивним, називається бієктивним. При бієктивному відображенні відбувається "накладання" множини на множину. У цьому разі кажуть, що між множинами і існує взаємно однозначна відповідність (рис.3).

Якщо є взаємно однозначним відображенням, а , то в цьому випадку говорять, що відображення є відображенням множини на саму себе (рис.4) або що воно є тотожним перетворенням (тотожним відображенням) множини.