В) Уравнения прямой, заданной двумя точками.

Согласно аксиомам геометрии через любые две точки проходит

единственная прямая.

З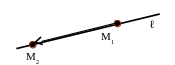 адача.

Дано:

М₁(x₁;y₁;z₁) ℓ

М₂(x₂;y₂;z₂) ℓ

Составить уравнение прямой ℓ. Рис. 15

Решение.

В данном случае - направляющий вектор прямой ℓ, а в качестве точки М₀ возьмём точку М₁. Вектор имеет координаты тогда, если ≠0, ≠0, ≠0 имеем

(18)

Уравнения (15) ─ уравнения прямой, заданной двумя точками.

Г) Уравнение прямой, заданной как линия пересечения двух плоскостей.

В пространстве нельзя задать прямую точкой и вектором нормали, так как эти данные не определяют положение прямой в пространстве единственным образом. (см. Рис. 16) В тоже время, если в пространстве даны две не параллельные плоскости, то их линия пересечения ─ прямая, определённая единственным образом.

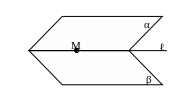Задача

Дано: α∩β = ℓ

α: А₁ х+В₁ у+С₁ z+D₁ =0

β: А₂ х+В₂ у+С₂ z+D₂ =0.

Составить уравнени прямой ℓ Рис. 16

Решение

Так как точка М, принадлежащая прямой ℓ = α ∩ β, то её координаты одновременно удовлетворяют как уравнению плоскости α так и уравнению плоскости β, то есть удовлетворяет системе уравнений

(19)

Система уравнений (19) называется уравнением прямой, заданной

как линия пересечения двух плоскостей.

Возникает вопрос. Как от уравнениям прямой (19) перейти к каноническим уравнениям (16)?

Для того, чтобы записать канонические уравнения прямой, необходимо знать координаты хотя бы одной точки, принадлежащей этой прямой и координаты направляющего вектора прямой. Эта проблема решается довольно просто. Координаты любой точки, принадлежащей прямой, заданной уравнениями (19), должны являться решением системы уравнений (19). Система уравнений (19) допускает бесчисленное множество решений, так как число неизвестных в этой системе больше числа уравнений. Чтобы найти какое-то решение этой системы одной из переменных дают произвольное значение, а две остальные находят в результате решения системы уравнений (19), в которую подставлено значение выбранной переменной.

Для определения координат направляющего вектора прямой, заданной уравнениям (19), заметим, что направляющий вектор прямой параллелен как плоскости α, так и плоскости β. Это означает, что координаты направляющего вектора прямой должны являться решением системы уравнений

(20)

Выделив р₃ в качестве свободного неизвестного, используя правило Крамера, получим решение системы уравнений (20) в виде:

. Полагая получим: для координат направляющего вектора прямой следующие выражения .