3.2. Практичний розрахунок призматичної балки на змінній пружній основі

3.2.1. Розрахункові залежності для елементів згину балки

Розглянемо практичне застосування МСР до задачі згину одно прогонної призматичної балки на змінній пружній основі (рис.3.7), яка наближено моделює згин поздовжніх фундаментних балок під головним двигуном (ГД) перекриття машинного відділення (рис. 1.1). Диференціальне рівняння згину такої балки має вигляд

, (3.10)

з граничними умовами при пружному затисненні опорних перерізів балки

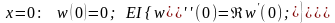(3.11)

де 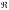– коефіцієнт жорсткості пружного затиснення, чисельно рівний опорному моменту при виникненні одиничного кута повороту у пружному затисненні.

Рис.3.7. Розрахункова схема призматичної балки на змінній пружній основі

Вважається, що балка завантажена рівномірними силами ваги ГД q_ГД на певній частині довжини прогону балки l₁<x<l₂ та лінійно змінними силами підтримання q_г.с(x).

У розрахунках більш зручним є використання коефіцієнта опорної пари 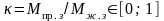, який зв’язаний з коефіцієнтом жорсткості формулою 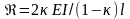, і тоді граничні умови (3.11) перепишуться так

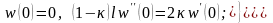(3.12)

У даній РГР погонний коефіцієнт жорсткості змінної пружної основи представлено залежністю k(x)=k₀(1+Δk(x/l)³), а зовнішнє поперечне навантаження від гідростатичного тиску забортної води на перекриття та ваги ГД – залежністю q(x)=q_г.с(x)+q_ГД(x)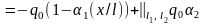 , де значком Бубнова || вказано інтервал дії сил ваги ГД на інтервалі [l₁, l₂].

Диференціальне рівняння (3.10) та граничні умови (3.12) утворюють відповідну крайову задачу БМК. Величини κ, k₀, Δk, α₁, l₁ та α₂, l_2, належать до вихідних даних при чисельних розрахунках, величини EІ, l та q₀ буде використано у розмірних множниках елементів згину (див нижче).

Оскільки диференціальне рівняння зі змінними коефіцієнтами (3.10) не можна інтегрувати точно, то потрібно використати наближені методи, зокрема чисельний метод скінченних різниць. Для практичного застосування МСР слід розбити довжину балки вузловими точками на певне число інтервалів n з довжиною h=l/n, пронумерувавши вузлові точки та інтервали, як показано на рис. 3.2. Використавши для похідних від прогину балки потрібні формули з (3.3), отримаємо замість диференціальних співвідношень крайової задачі алгебраїчні скінченно-різничні формули для безрозмірного прогину 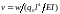у вигляді:

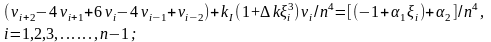(3.13)

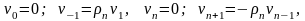(3.14)

де координата ξ_i=x_i/l=i/n та позначено множники 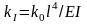та .

Рівняння (3.13) у точці і=1 буде містити значення v_-1, а у точці n-1 – значення v_n+1, які є фіктивними у поза контурних точках балки і які слід визначати із граничних умов (3.14) через прогини у внутрішніх точках балки.

Таким чином, буде створена система лінійних алгебраїчних рівнянь (СЛАР) відносно множини вузлових значень прогинів v_i, i=1,2,….,n-1, яка замінила диференціальне рівняння граничної задачі відносно неперервної функції w(x). У цьому фактично і полягає сутність методу скінченних різниць. СЛАР розв’язують одним із відомих методів (в ручну при n=4 – підстановками, методами Крамера, оберненої матриці тощо, або у загальному випадку – із застосуванням комп’ютерних програм, наприклад, у пакеті MathCard) і отримують чисельні значення для безрозмірних прогинів v_i, i=1,2,….,n-1. Далі можуть бути визначені інші елементи згину балки – кути повороту, згинальні моменти та зрізувальні сили уздовж балки за наступними формулами скінченних різниць:

, (3.15)

де i=0,1,2,….,n, та в усіх залежностях в (3.15) перші вирази у круглих дужках відіграють роль розмірних величин, а θ_i, μ_i, η_i є безрозмірні розрахункові значення відповідних елементів згину.

3.2.2. Порядок розрахунків елементів згину балки

З м і с т з а в д а н н я. Для заданої призматичної балки на змінній пружній основі (див. рис. 3.7) методом скінченних різниць розрахувати елементи згину: прогини, кути повороту, згинальні моменти та зрізувальні сили в рівновіддалених перерізах балки, прийняти крок дискретизації h=l/4, l/6, l/8. При кроці l/4 розрахунок також виконати вручну. Побудувати у масштабі епюри вказаних елементів згину балки.

Порівняти максимальні значення елементів згину балки з довідковими даними для балок на еквівалентній постійній пружній основі та оцінити похибку розрахунків за ТТЗБ.

Вихідними даними для розрахунків є наступні величини:

κ – коефіцієнт опорної пари пружних затиснень;

k₀ – постійна частина погонного коефіцієнта жорсткості пружної основи (задається у безрозмірному вигляді );

Δk – змінна частина погонного коефіцієнта жорсткості пружної основи;

α₁ та α₂ – допоміжні множники для визначення сил тиску води та ваги ГД;

l₁ та l₂ – визначають інтервал дії сил ваги від ГД (задають в долях від довжини балки l).

Інші фізичні характеристики балки входять у розмірні множники і визначення не потребують.

Рекомендується наступна послідовність виконання РГР.

1. Зобразити графічно розрахункову схему балки з урахуванням заданих співвідношень для геометричних розмірів та навантажень на балку. Окремо розрахувати в точках x/l=0; 0,25; 0,50; 0,75; 1,0 безрозмірні значення коефіцієнта жорсткості пружної основи та побудувати у масштабі графік його зміни уздовж балки.

2. Нанести на схемі балки точки дискретизації при довільному значенні n та виписати розрахункові залежності у термінах скінченних різниць згідно формул (3.13) та (3.14).

3. Прийняти значення n=4 та виписати СЛАР у явному вигляді при i=1,2,3. З граничних умов визначити прогини у фіктивних точках і виключити їх з СЛАР та привести систему рівнянь до канонічного вигляду. Тим чи іншим методом розв’язати СЛАР і отримати прогини балки у точках дискретизації (з обов’язковою перевіркою розв’язку при ручних розрахунках).

4. Виписати формули для інших елементів згину (3.15) і за відомими значеннями прогинів у точках дискретизації розрахувати їх чисельні значення. У масштабі побудувати епюри елементів згину балки (див. нижче рис. 3.8).

5. Прийняти послідовно значення n=6 та 8 і виписати відповідні СЛАР у явному вигляді. За допомогою комп’ютерних засобів отримати розв’язки СЛАР і далі повторити дії згідно п. 4.

6. Порівняти та проаналізувати результати розрахунків при різних значення числа точок дискретизації балки n. Побудувати графіки залежності максимальних значень елементів згину за числом n=4; 6; 8 (типу рис. 2.3).

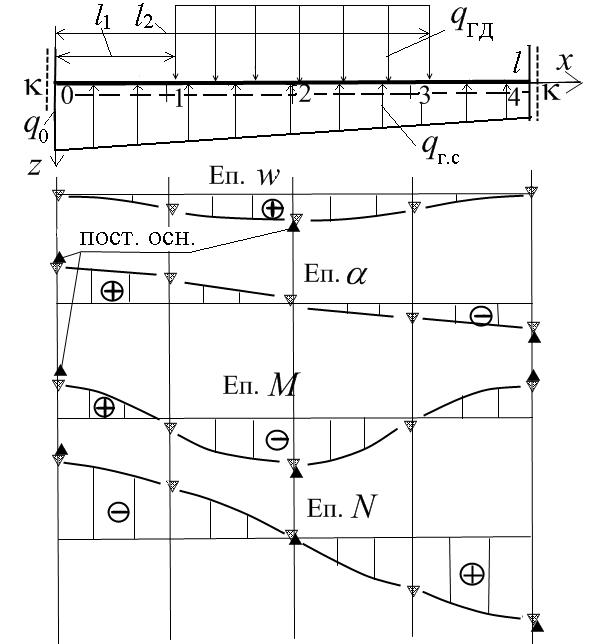
Рис. 3.8. Епюри елементів згину балки на змінній пружній основі