2.3. Розрахунок пластини за технічною теорією згину балок

Компоненти НДС пластини можна наближено визначити, прийнявши розрахункову схему балки-стінки з довжиною прогону а, поперечним розмірами txb, t=1 та шарнірними умовами закріплення на опорах. При цьому дійсне навантаження апроксимується рядом Фур’є (2.17) з коефіцієнтами згідно (2.18), див. рис. 2.2.

Рис. 2.2. Розрахункова схема балки-стінки для пластини

Геометричні характеристики поперечного перерізу балки стінки будуть такими:

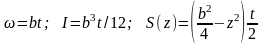, (2.19)

де ω_c – площа поперечного перерізу; І– момент інерції площі перерізу відносно нейтральної осі (див. рис. 2.2); S(z) – статичний момент відсіченої частини площі f(z) відносно нейтральної осі.

Визначення прогину балки від згину зводиться до розв’язання крайової задачі:

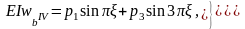, (2.20)

Розв’язок даної крайової задачі шукають за виглядом правої частини і остаточно будемо мати:

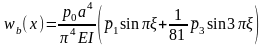, (2.21)

де .

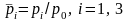Прогини балки-стінки можна уточнити, додавши прогини від деформації зсуву, які визначаються залежністю [1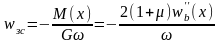, 2]

. (2.22)

У розрахункових перерізах остаточно формули для елементів згину балки-стінки мають наступний вид.

Прогини по середині довжини балки дорівнюють:

- від згину 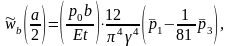(2.23)

- від зсуву 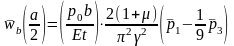, (1.24)

- повний прогин 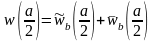. (1.25)

Нормальні напруження σ_x(z) на середині довжини балки дорівнюють

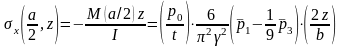. (1.26)

На опорах балки маємо:

- переміщення точок перерізу від згину уздовж осі Ox:

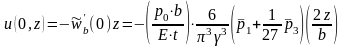, (1.27)

- дотичні напруження τ_xy(z):

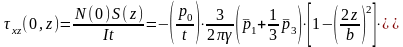. (1.28)

Зазначимо, що у формулах (1.24) – (1.29) перші множники у круглих дужках мають зміст розмірних величин і в розрахунках не беруться до уваги.

Рис. 2.3 Рис.2.4

На рис. 2.3 та 2.4 наведено приклади графіків, які потрібно побудувати за результатами усіх розрахунків у РГР. Усі графіки будують у масштабі.

Таким чином, у результаті виконання даної розрахунково-графічної роботи студенти оволодіють технікою застосування методу розділення змінних при розв’язанні крайових задач БМК, отримають, а також зможуть проаналізувати чисельні результати стосовно збіжності рядів у розв’язках та зможуть порівняти розв’язки для елементів НДС пластини у рамках плоскої задачі та за більш грубою схемою балки-стінки.

Запитання для самоконтролю

1. Вказати особливості формулювання плоскої задачі теорії пружності (характер зовнішніх навантажень, компоненти тензора напружень, функція напружень).

2. Вказати як формулюється крайова задача у плоскій задачі для пластин (основне рівняння та граничні умови для сторін пластини).

3. Сформулювати сутність методу розділення змінних (МРЗ) для розв’язання крайових задач БМК. Показати застосування методу для отримання розв’язку рівняння Лапласа. Вказати роль граничних умов в МРЗ.

4. Вказати техніку застосування методу розділення змінних в задачах вібрації суднових балок.

5. Показати техніку застосування методу розділення змінних для розв’язання бігармонічного рівняння. Вказати чому потрібно приймати додаткові припущення для даного рівняння.

6. Вказати корисність використання функцій Калманка у розв’язках плоскої задачі для пластин.

7. Вказати, які граничні умови - силові чи кінематичні потрібно записати для пластини при виконанні відповідної РГР.

8. Показати, як потрібно визначати сталі інтегрування у розв’язку плоскої задачі за зміною y.

9. Показати, як можна отримати наближену оцінку для компонентів НДС пластини у плоскій задачі при застосуванні залежностей ТТЗБ.

10. Вказати, як можна уточнювати наближений розв’язок при застосування МРЗ.