
- •А. М. Сердюченко, ю.П. Кочанов навчально-методичні вказівки до виконання розрахунково-графічних робіт з дисципліни «математичні моделі та чисельні методи бмк та мпс»
- •Наближені аналітичні методи в бмк
- •Прямі диференціальні методи бмк
- •Варіаційні методи бмк
- •1.3. Асимптотичні методи бмк
- •2. Розрахунок плоского напруженого стану у тонких суднових пластинах методом розділення змінних
- •Основні залежності плоского напруженого стану для пластин та метод розділення змінних
- •2.2. Вихідні дані та послідовність розрахунку компонентів плоского ндс пластини
- •2.3. Розрахунок пластини за технічною теорією згину балок
- •Запитання для самоконтролю
- •3. Розрахунок згину суднових балок методом скінченних різниць
- •3.1. Теоретичні положення методу скінченних різниць у бмк
- •3.2. Практичний розрахунок призматичної балки на змінній пружній основі
- •3.3. Наближений розрахунок призматичної балки на постійній пружній основі
- •Питання для самоконтролю
- •4. Розрахунок згину суднових балок методом скінченних елементів
- •4.1. Теоретичні положення методу скінченних елементів у бмк
- •4.2. Практичний розрахунок непризматичної одно прогонної балки на змінній пружній основі мсе
- •Питання для самоконтролю
- •Чисельні методи для початкових задач бмк
- •Питання для самоконтролю
- •Висновки
- •Список літератури Підручники
- •Посібники
- •Монографії
- •Довідники
2. Розрахунок плоского напруженого стану у тонких суднових пластинах методом розділення змінних
Плоский напружений стан виникає у тонких пласких пластинах при дії зовнішніх навантажень у площині пластин, прикладених уздовж їх сторін. У таких умовах працюють, наприклад, пластини обшиви борту та настилів палуб і стінки поздовжніх міцних балок суднового корпусу, до яких прикладені напруження від загального згину судна та при відсутності місцевих поперечних навантажень від тиску води чи вантажу. Але при виконанні спеціальних умов стосовно форми пружного тіла та діючих навантажень плоский напружено-деформівний стан (НДС) може виникати і у тривимірних пружних тілах [1, 2, 4]. У даному розділі плоский НДС розглядається для тонких суднових пластин при спеціальних умовах їх закріплення – підвісі на ідеально гнучких міцних в’язях (див. нижче рис. 2.1). Такі умови використано для спрощення розрахунків у даній задачі.
Математично плоский напружений стан описується крайовою задачею, яка включає бігармонічне диференціальне рівняння у частинних похідних відносно функції напружень в області пластини та силові граничні умови на сторонах пластини. Розв’язок крайової задачі потрібно отримувати із застосуванням методу розділення змінних (відому у математиці також як метод Фур’є [10, 13]). Згідно даному методу розв’язки, які залежать від двох чи більше незалежних змінних, наприклад, φ(x,y), w(x,t), u(x,y,z) шукають наступним чином: φ(x,y)=X(x)·Y(y), w(x,t)=X(x)·T(t), u(x,y,z)=X(x)·Y(y)·Z(z), де X(x), Y(y) і т. ін. є невідомі функції, кожна з яких залежать тільки від однієї незалежної змінної. Це дає змогу вихідні рівняння у частинних похідних розділити на незалежні звичайні диференціальні рівняння для кожної функції. Даний метод суттєво спрощує алгоритм розв’язку багатьох крайових та початково-крайових задач математичної фізики і БМК зокрема.
Основні залежності плоского напруженого стану для пластин та метод розділення змінних
При реалізації плоского НДС тензор напружень спрощується до вигляду
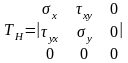 ,
(2.1)
,
(2.1)
компоненти якого задовольняють наступним рівнянням рівноваги елементарного паралелепіпеда [1, 2, 4]
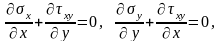 (2.2)
(2.2)
та рівнянням сумісності деформацій (рівнянням Сен-Венана) [1, 2]
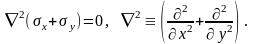 (2.3)
(2.3)
Ще у другій половині 19-го століття А.Ері запропонував ввести до розгляду так звану функцію напружень φ(x,y) для визначення напружень у тензорі (2.1)
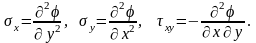 (2.4)
(2.4)
Залежності (2.4) точно задовольняють рівнянням рівноваги (2.2) та приводять рівняння сумісності (2.3) до виду
 (2.5)
(2.5)
де
диференціальний оператор четвертого
порядку за незалежними змінними
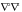 називають бігармонічним.
називають бігармонічним.
Рівняння (2.5) далі розглядається як основне рівняння для розв’язання задачі. Воно повинно бути доповнене граничними умовами на сторонах пластини. У залежності від характеру закріплення та завантаження сторін пластини це можуть бути або кінематичні граничні умови для переміщень (наприклад, u=v=0), або силові граничні умови для напружень (наприклад, σx=τxy=0). Конкретно для розрахункової схеми пластини, зображеної на рис.2.1, маємо такі граничні умови:
1)
на сторонах x=0
та x=a
відсутні нормальні напруження: σx=0,
але
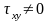 ;
;
2) на стороні y=0 відсутні як нормальні, так дотичні напруження: σx=τxy=0;
3) на стороні y=b має місце рівність σy=pνy=–p(x), а також умова τxy=0.

Рис. 2.1. Розрахункова схема пластини
Крім того, маємо інтегральні умови рівноваги пластини (з урахуванням симетрії задачі)
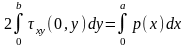 .
(2.6)
.
(2.6)
Як видно, при даних закріпленнях пластини усі граничні умови є силовими. З урахуванням формул (2.4) їх можна переписати відносно функції напружень φ(x,y).
Перейдемо тепер до методу розділення змінних у даній задачі, згідно якому представимо функцію напружень добутком φ(x,y)=X(x)·Y(y), де X(x), Y(y) є нові шукані функції. Для їх визначення підставимо даний розв’язок у бігармонічне рівняння (2.5) та поділимо його на добуток X(x)Y(y)≠0, що дає наступне рівняння
 (2.7)
(2.7)
де верхніми індексами позначено похідні відповідно за змінними x та y.
Рівняння
(2.7) безпосередньо не можна розділити
за функціями X(x)
та Y(y)
і тому приймемо додаткове припущення,
що
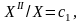
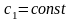 .
Тоді далі матимемо співвідношення
.
Тоді далі матимемо співвідношення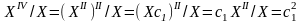 .
Дане припущення породжує звичайне
диференціальне рівняння
.
Дане припущення породжує звичайне
диференціальне рівняння
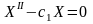 ,
яке має добре відомий розв’язок
,
яке має добре відомий розв’язок
 (2.8)
(2.8)
де сталі інтегрування Ac,s визначаються із граничних умов на вертикальних сторонах пластини.
Перші
граничні умови при
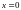 та
та
 вимагають, щоб
вимагають, щоб
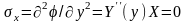 на даних сторонах, а це можливо тільки
при значенні сталої інтегрування
на даних сторонах, а це можливо тільки
при значенні сталої інтегрування
 (можна також прийняти As=1)
та значенні константи
(можна також прийняти As=1)
та значенні константи
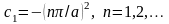 .
Таким чином, розв’язки за змінною
.
Таким чином, розв’язки за змінною
 для даної пластини з підвісами можна
записати у вигляді (з використанням
безрозмірної координати ξ=x/a)
для даної пластини з підвісами можна
записати у вигляді (з використанням
безрозмірної координати ξ=x/a)
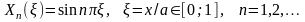 .
(2.9)
.
(2.9)
Тоді
звичайне диференціальне рівняння для
другої шуканої функції
 за змінною y
прийме наступний вигляд (з використанням
безрозмірної координати η=y/b)
за змінною y
прийме наступний вигляд (з використанням
безрозмірної координати η=y/b)
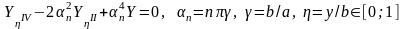 .
(2.10)
.
(2.10)
Розв’язок
звичайного диференціального рівняння
(2.10) також шукають підстановкою Ейлера
Y(η)=Bexp(βη),
що дає характеристичне рівняння
 ,
яке має два кратні дійсні корені
,
яке має два кратні дійсні корені
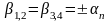 .
Тому остаточно будемо мати розв’язок
.
Тому остаточно будемо мати розв’язок
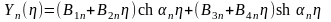 ,
(2.11)
,
(2.11)
де Bjn – сталі інтегрування, які визначають з граничних умов на сторонах пластини y=0; b, а лінійні за координатою η члени у дужках обумовлені кратністю коренів.
Але дана форма розв’язку не є зручною при отриманні старших похідних у практичних розрахунках і тому у середині 20-го століття А.С. Калманок запропонував ввести спеціальні функції – функції Калманка, як певні комбінації гіперболічних функцій у вигляді [1, 2, 6]
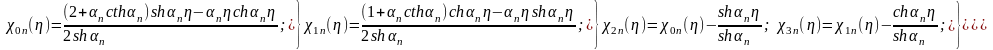 (2.12)
(2.12)
Тоді остаточно розв’язок для функції напружень запишеться так
 .
(2.13)
.
(2.13)
Відповідно поле напружень σx(x,y), σy(x,y), τxy(x,y) визначається формулами (2.4) і остаточно маємо залежності
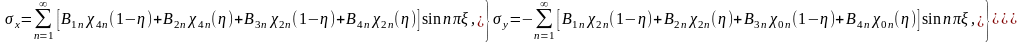 ,
(2.14)
,
(2.14)
а поле переміщень u(x,y) та v(x,y) визначається із застосуванням рівнянь Коші та закону Гука при плоскому НДС [1, 2] і остаточно також будемо мати
 (2.15)
(2.15)
де позначено допоміжні функції Калманка
 (2.16)
(2.16)
Функції Калманка χin(η) представлено таблицями у [2] та у скороченому варіанті нижче у п. 2.2 при n=1 та певними значеннями відношення сторін пластини з метою їх використання при виконанні ручних розрахунків компонентів НДС пластини..
