
- •А. М. Сердюченко, ю.П. Кочанов навчально-методичні вказівки до виконання розрахунково-графічних робіт з дисципліни «математичні моделі та чисельні методи бмк та мпс»
- •Наближені аналітичні методи в бмк
- •Прямі диференціальні методи бмк
- •Варіаційні методи бмк
- •1.3. Асимптотичні методи бмк
- •2. Розрахунок плоского напруженого стану у тонких суднових пластинах методом розділення змінних
- •Основні залежності плоского напруженого стану для пластин та метод розділення змінних
- •2.2. Вихідні дані та послідовність розрахунку компонентів плоского ндс пластини
- •2.3. Розрахунок пластини за технічною теорією згину балок
- •Запитання для самоконтролю
- •3. Розрахунок згину суднових балок методом скінченних різниць
- •3.1. Теоретичні положення методу скінченних різниць у бмк
- •3.2. Практичний розрахунок призматичної балки на змінній пружній основі
- •3.3. Наближений розрахунок призматичної балки на постійній пружній основі
- •Питання для самоконтролю
- •4. Розрахунок згину суднових балок методом скінченних елементів
- •4.1. Теоретичні положення методу скінченних елементів у бмк
- •4.2. Практичний розрахунок непризматичної одно прогонної балки на змінній пружній основі мсе
- •Питання для самоконтролю
- •Чисельні методи для початкових задач бмк
- •Питання для самоконтролю
- •Висновки
- •Список літератури Підручники
- •Посібники
- •Монографії
- •Довідники
1.3. Асимптотичні методи бмк
Асимптотичні методи (іншими словами, методи теорії збурень, методи малого параметру) ґрунтуються на тому, що ускладнення в диференціальних рівняннях чи граничних умовах крайової задачі є відносно малими і можуть бути оцінені певними числом – малим додатнім параметром 0<ε<<1. Часто такий малий параметр ε утворюється при переході до безрозмірних величин та змінних задачі, але є багато прикладів, коли його вводять у формулювання задачі штучно [10].
У нашому прикладі для рівняння (1.1) будемо вважати, що не призматичність балки ∆I(x)=I(x)-I0 та коефіцієнт змінності погонної жорсткості пружної основи Δk є відносно малими у порівнянні до призматичної балки з моментом інерції I0 на постійній пружній основі з коефіцієнтом жорсткості k0. Тоді можна записати, що ∆I(x)/I0 ~ε та Δk/k0~ε, а рівняння згину (1.1) переписати у вигляді
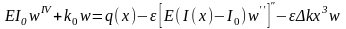 ,
(1.17)
,
(1.17)
де малі збурення у задачі (не призматичність балки на змінність пружної основи) перенесено у праву частину рівняння.
Найпростішим
прикладом на множині методів малого
параметру є метод
послідовних наближень з
неявним використанням малого параметру
задачі.
За
даним методом у базовому нульовому
наближенні збурення відкидаються і
розв’язується базове диференціальне
рівняння
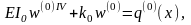
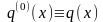 ,
для якого не виникає ускладнень з
розв’язком [1 - 4]. Далі отриманий розв’язок
w(0)(x)
підставляють у праву частину
диференціального рівняння (1.17) і у
першому наближенні шукають розв’язок
рівняння
,
для якого не виникає ускладнень з
розв’язком [1 - 4]. Далі отриманий розв’язок
w(0)(x)
підставляють у праву частину
диференціального рівняння (1.17) і у
першому наближенні шукають розв’язок
рівняння
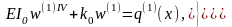 (1.18).
(1.18).
Після отримання розв’язку рівняння w(1)(x) він аналогічним чином підставляється у праву частину диференціального рівняння (1.17) і шукається розв’язок w(2)(x) і так далі.
Важливим у даному методі є питання збіжності розв’язків w(j)(x), j=1,2,…. до певного прогину w(x) і тут можливі чотири варіанти. У першому найкращому варіанті послідовність розв’язків w(j)(x) збігається і на певному наближенні можна завершити обчислення, виходячи із прийнятної точності остаточних результатів (абсолютна збіжність). У другому гіршому варіанті послідовність розв’язків w(j)(x) спочатку збігається, а потім починає розбігатися і з кожним наступним наближенням розбіжність тільки посилюється (асимптотична збіжність). Тоді у якості остаточного результату можна взяти значення w(k)(x), після якого вже починається розбіжність. У третьому ще гіршому варіанті значення w(j)(x) здійснюють незатухаючі коливання відносно деякого середнього значення wc(x), яке й можна прийняти у якості наближеного розв’язку задачі (умовна збіжність). Нарешті у четвертому найгіршому варіанті збіжність взагалі відсутня, починаючи з перших ітерацій, і це означає повну непридатність метода послідовних наближень при розв’язанні даній задачі. На рис. 1.4 якісно проілюстровано дані типи збіжності. Тут збіжність розуміється як рівномірна збіжність |w(j+1)(x)–w(j)(x)|→0, а розбіжність – як |w(j+1)(x)–w(j)(x)|→∞ при зростанні порядку наближення.

Рис.1.4. Різні характери збіжності в методах малого параметру; (- - - -) асимптотичний розв’язок задачі
Крім зазначеного метод послідовних наближень має ще один недолік – у кожному наближенні повторно отримуються результати попереднього наближення і це робить метод трудомістким у достатньо складних задачах. Тому було розроблено більш ефективні варіанти на множині асимптотичних методів, один з яких – метод малого параметру - полягає у наступному. Розв’язок диференціального рівняння (1.17) залежить також і від малого параметру ε, тобто w=w(x, ε) і далі приймається, що дана залежність є аналітичною і її можна представити степеневим рядом [10]
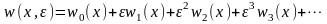 ,
(1.19)
,
(1.19)
де wk(x), k=0,1,2,… – невідомі функції, які потрібно визначати.
Також оскільки степені малого параметру досить швидко зменшуються (наприклад, при ε=0,2 маємо ε2=0,04; ε3=0,008 і т.д.), тому є надія, що ряд буде швидко збігатися і потрібно отримати тільки декілька перших членів ряду.
Для
визначення невідомих функцій wk(x)
у ряді (1.19) його підставляють у
диференціальне рівняння (1.17), групують
члени з однаковими ступенями за малим
параметром εk,
k=0,1,2,….
так що диференціальне рівняння отримує
наступну (операторну) форму запису
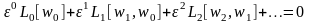 .
При довільному значенні малого параметру
ε≠0
рівність нулю буде отримано, якщо кожний
з виразів Lk[wj]
у рівнянні дорівнює нулю, і це породжує
рекурентну послідовність диференціальних
рівнянь у збуреннях для визначення
невідомих функцій wk(x).
У нашому випадку матимемо таку
послідовність
.
При довільному значенні малого параметру
ε≠0
рівність нулю буде отримано, якщо кожний
з виразів Lk[wj]
у рівнянні дорівнює нулю, і це породжує
рекурентну послідовність диференціальних
рівнянь у збуреннях для визначення
невідомих функцій wk(x).
У нашому випадку матимемо таку
послідовність
 ,
(1.20)
,
(1.20)
У даному методі не потрібно повторно відновлювати результати попередніх наближень, але проблема збіжності ряду залишається такою ж. Практичний досвід показує [10], що у більшості задач має місце другий із вказаних вище варіантів збіжності. Але при зменшенні чисельного значення малого параметру ε порядок початку розбіжності все далі відсувається до вищих наближень і ряд точно збігається лише при умові, що ε →0. Тому такі ряди й назвали асимптотичними, а відповідно й методи отримали таку ж назву.
У алгоритмах асимптотичних методів потрібно для кожного наближення отримувати розв’язки диференціального рівняння при довільному (приведеному) поперечному навантаженні qj(x). З курсу БМК відомо [1 - 4], що неоднорідна частина розв’язку базового рівняння матиме простий вигляд qj(x)/k0, тільки коли поперечне навантаження є поліном не вище третього порядку. Тому на завершення даного розділу наведемо метод Коші для отримання неоднорідного розв’язку при довільному поперечному навантаженні на балку [12].
Згідно даному методу неоднорідна частина розв’язку визначається так званим інтегралом у згортках виду
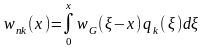 ,
(1.21)
,
(1.21)
де
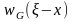 є так звана функція Гріна задачі як
однорідний розв’язок диференціального
рівняння
є так звана функція Гріна задачі як
однорідний розв’язок диференціального
рівняння
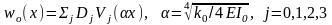 ,
у якому сталі інтегрування Dj
потрібно визначити при наступних
початкових умовах
,
у якому сталі інтегрування Dj
потрібно визначити при наступних
початкових умовах
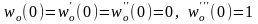 .
Врахувавши відомий зв'язок між функціями
Пузиревського Vj(αx)
при диференціюванні та їх значення при
х=0
[1,
2], отримаємо для сталих інтегрування
значення D0=D1=D2=0,
D3=1/2√2α.
Тоді функція Гріна отримає вид
.
Врахувавши відомий зв'язок між функціями
Пузиревського Vj(αx)
при диференціюванні та їх значення при
х=0
[1,
2], отримаємо для сталих інтегрування
значення D0=D1=D2=0,
D3=1/2√2α.
Тоді функція Гріна отримає вид
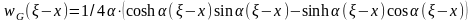 .
(1.22)
.
(1.22)
Інтеграл у розв’язку (1.21) у загальному випадку розраховується чисельними методами.
На завершення ще раз підкреслимо, що характер збіжності асимптотичного ряду (1.13) суттєво залежить від поведінки добутку εjwj(x) при зростанні порядку наближення j. Якщо у наближеннях |wj+1(x)|<|wj(x)|, то ряд буде безумовно збігатися, також якщо |wj+1(x)|>|wj(x)|, то ряд знову буде збігатися, але повільніше. Проте, якщо |wj+1(x)|>>|wj(x)|, то буде виникати розбіжність або відразу, або після певного порядку наближення. Тому більшість асимптотичних методів на множині методів теорії збурень як раз і було розроблено для подолання розбіжностей у певних класах задач [10].
Запитання для самоконтролю
Вказати основні фізичні моделі для суднових конструкцій у БМК.
Вказати основні математичні моделі (задачі), які розглядають у БМК.
Пояснити, як математично формулюються крайові, початкові та початково-крайові задачі БМК.
Дати означення для точних та наближених методів для розв’язання задач БМК.
Вказати відмінність між аналітичними та чисельними методами БМК.
Вказати основний принцип, на якому ґрунтуються наближені чисельні методи БМК. Навести приклади таких методів.
Вказати основні сімейства наближених аналітичних методів для розв’язання крайових задач БМК та вказати принцип їх класифікації.
Пояснити сутність проекційного методу наближеного визначення прогину балки та дати характеристику системи фундаментальних функцій у розв’язку і вказати невідомі у даному методі.
Пояснити у чому полягають основні труднощі при виборі фундаментальних функцій та рекомендації Ю.П.Кочанова для їх подолання.
Пояснити на конкретному прикладі згину балки сутність методу коллокацій та техніку його застосування. Вказати приналежність методу згідно класифікації.
Пояснити на конкретному прикладі згину балки сутність методу Бубнова-Гальоркіна та техніку його застосування. Вказати приналежність методу згідно класифікації.
Пояснити на конкретному прикладі згину балки сутність методу найменших квадратів та техніку його застосування. Вказати приналежність методу згідно класифікації.
Пояснити на конкретному прикладі згину балки сутність методу Рітца та техніку його застосування. Вказати приналежність методу згідно класифікації.
Пояснити на конкретному прикладі згину балки сутність методу послідовних наближень та умови і техніку його застосування. Вказати приналежність методу згідно класифікації.
Пояснити на конкретному прикладі згину балки умови застосування та сутність методу малого параметру та умови і техніку його застосування.
