2. Варіаційні методи бмк

У варіаційних методах у якості вихідних використовують не диференціальні рівняння задачі, а певні функціонали, які зв’язані з формулюванням даної задачі (у математиці функціоналами називають певні числа, які визначаються на множині функцій, у задачах БМК в основному погинів) [2, 8]. Розглянемо далі два приклади варіаційних методів, розпочавши з найбільш простого методу найменших квадратів, згідно якому у якості функціонала, який потрібно мінімізувати з метою отримання найкращого наближення для розв’язку 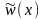, приймають сумарний квадрат похибки розв’язку уздовж балки . 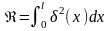Згідно виразу (1.6) для похибки даний функціонал буде містити коефіцієнти ряду (1.2), варіації яких змінюють прогини балки, і тому будемо визначати ці коефіцієнти з умови мінімуму сумарної похибки за варіаціями даних коефіцієнтів (рис. 1.3)

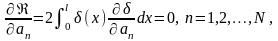(1.13)

яка остаточно після проведення операцій диференціювання похибки (1.6) за коефіцієнтами a_n та інтегрування уздовж балки знову дасть СЛАР типу (1.8).

Рис. 1.3. Умови мінімуму функціоналу на дійсному прогині

Більш ефективним є метод Рітца, який ґрунтується на використанні принципу можливих переміщень для пружних систем. Метод Рітца виходить з функціоналу у вигляді повної роботи, яку виконують зовнішні та внутрішні сили на пружних переміщеннях балки (U-V), де V є потенціальна енергія деформування балки та пружної основи, як міра роботи внутрішніх сил, та U є робота зовнішніх сил, прикладених до балки. Вираз (V-U) в БМК ще називають повною силовою функцією пружної системи і він є більш зручним для розрахунків [1, 2].

При дії заданих навантажень пружні переміщення балки виникають завжди із мінімальними затратами енергії, тоді як для усіх інших можливих (віртуальних) переміщень, які не порушують умови закріплення балки, такі затрати енергії на деформування завжди будуть більшими. На цьому і ґрунтується принцип можливих переміщень.

Тоді в околі дійсних переміщень пружної системи має місце мінімум силової функції, який математично визначається рівністю нулю першої похідної за коефіцієнтами a_n

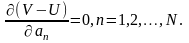(1.14)

Дана умова як раз і забезпечує найкраще наближення для розв’язку (1.2).

Якщо обмежитись лише згинальними деформаціями балки, то потенціальна енергія згину балки та пружної основи визначається залежністю

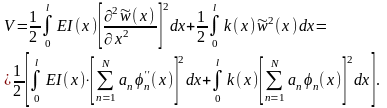(1.15)

Робота зовнішніх поперечних сил q(x) визнається формулою

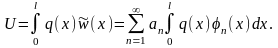(1.16)

Підстановка даних залежностей в умову мінімуму (1.14) з утриманням тільки певної кількості членів ряду для прогинів балки та виконання усіх операцій диференціювання та інтегрування знову призводить остаточно до СЛАР відносно коефіцієнтів a_n типу (1.8).

Зазначимо ще, що при наявності деформівних опорних закріплень балки (пружних опор та пружних затиснень) у повну силову функцію також потрібно включати енергію деформування таких опор. Також при не можливості підібрати адекватну систему фундаментальних функцій для заданої схеми закріплень балки потрібно використовувати метод Ю.П. Кочанова у загальному вигляді (1.10).