
- •А. М. Сердюченко, ю.П. Кочанов навчально-методичні вказівки до виконання розрахунково-графічних робіт з дисципліни «математичні моделі та чисельні методи бмк та мпс»
- •Наближені аналітичні методи в бмк
- •Прямі диференціальні методи бмк
- •Варіаційні методи бмк
- •1.3. Асимптотичні методи бмк
- •2. Розрахунок плоского напруженого стану у тонких суднових пластинах методом розділення змінних
- •Основні залежності плоского напруженого стану для пластин та метод розділення змінних
- •2.2. Вихідні дані та послідовність розрахунку компонентів плоского ндс пластини
- •2.3. Розрахунок пластини за технічною теорією згину балок
- •Запитання для самоконтролю
- •3. Розрахунок згину суднових балок методом скінченних різниць
- •3.1. Теоретичні положення методу скінченних різниць у бмк
- •3.2. Практичний розрахунок призматичної балки на змінній пружній основі
- •3.3. Наближений розрахунок призматичної балки на постійній пружній основі
- •Питання для самоконтролю
- •4. Розрахунок згину суднових балок методом скінченних елементів
- •4.1. Теоретичні положення методу скінченних елементів у бмк
- •4.2. Практичний розрахунок непризматичної одно прогонної балки на змінній пружній основі мсе
- •Питання для самоконтролю
- •Чисельні методи для початкових задач бмк
- •Питання для самоконтролю
- •Висновки
- •Список літератури Підручники
- •Посібники
- •Монографії
- •Довідники
Наближені аналітичні методи в бмк
У даному розділі стисло розглянуто деякі наближені аналітичні обчислювальні методи, які достатньо широко застосовуються при розв’язанні крайових задач будівельної механіки корабля. У якості прикладу використаємо наступну задачу про згин непризматичної балки на змінній пружній основі
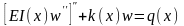 ,
(1.1)
,
(1.1)
з
граничними умовами жорсткого затиснення
на кінцях балки
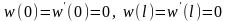 .
До даної задачі може бути зведено
розрахунок згину днищового перекриття
корпусу судна у машинному відділенні
(див. рис. 1.1). При цьому погонний коефіцієнт
жорсткості змінної пружної основи може
бути апроксимовано залежністю
.
До даної задачі може бути зведено
розрахунок згину днищового перекриття
корпусу судна у машинному відділенні
(див. рис. 1.1). При цьому погонний коефіцієнт
жорсткості змінної пружної основи може
бути апроксимовано залежністю
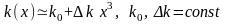 .
.

Рис. 1.1. Спрощена схема днищового перекриття корпусу судна у машинному відділенні та еквівалентна непризматична балка на змінній пружній опорі.
Значна кількість наближених аналітичних методів виходить із наступного способу визначення для прогину балки [1, 2, 5] (такий спосіб у математиці називають проекційним, оскільки він «проектує» прогини, як елементи функціонального простору неперервних функцій, у набори числових коефіцієнтів як елементів векторного простору)
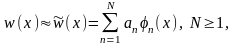 (1.2)
(1.2)
Де значок «~» тут і далі вказує на наближений розв’язок; an – невідомі коефіцієнти ряду, які розглядають як узагальнені переміщення пружної системи qn, та φn(x) – відомі координатні функції, які утворюють повну та фундаментальну систему функцій.
Ці
умови для систем функцій потрібні для
забезпечення збіжності ряду до будь
якого кінематично допустимого прогину
балки. Загалом дані функції потрібно
підбирати для кожної задачі з урахуванням
граничних умов на кінцях балки. Поширеними
є системи степеневих функцій
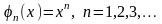 та тригонометричних функцій
та тригонометричних функцій
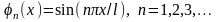 .
Для жорстко затисненої на опорах балки
при симетричному навантаженні прийнятною
є наступна система координатних функцій
.
Для жорстко затисненої на опорах балки
при симетричному навантаженні прийнятною
є наступна система координатних функцій
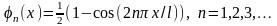 ,
а для консольної балки – система
координатних функцій
,
а для консольної балки – система
координатних функцій
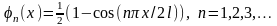 (див. рис. 1.2).
(див. рис. 1.2).

Рис. 1.2. Графіки для перших елементів у різних системах координатних функцій; а) степеневі, б) для шарнірно закріпленої балки, в) для консольної балки
Підібрати системи фундаментальних функцій, які б повністю задовольняли граничним умовам крайової задачі досить важко, а часто і неможливо. Тому поширеним є наступний спосіб запису прогину, запропонований проф. Кочановим Ю.П. з метою спрощення процедури підбору систем фундаментальних функцій у конкретних задачах [2, 5, 6]
 (1.3)
(1.3)
де перші коефіцієнти cm визначають через коефіцієнти an з граничних умов задачі.
Різні наближені методи відрізняються між собою вихідними ідеями та алгоритмами визначення невідомих коефіцієнтів an та сm. Вище їх було поділено на три множини – прямі диференціальні, варіаційні та асимптотичні методи. Розглянемо для кожної множини по два приклади наближених методів – простий та більш досконалий.
Прямі диференціальні методи бмк
На множині прямих диференціальних методів найпростішим за сутністю є метод коллокацій (від латинського слова “collocatio” – спільне розташування), який виходить з того, що диференціальне рівняння (1.1) задовольняється тільки на певній множині дискретних точок уздовж балки xk, k=1,2,3,….,N
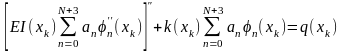 ,
(1.4)
,
(1.4)
де першу суму у виразі (1.3) включено для уніфікації у загальний ряд за n.
Набір рівнянь (1.4) фактично представляє собою систему лінійних алгебраїчних рівнянь (СЛАР) відносно коефіцієнтів an, з якої методами лінійної алгебри [14] (зокрема, методом визначників Крамера, методом Гауса тріангуляції матриці системи, методом оберненої матриці та інш.) можна отримати чисельні значення коефіцієнтів ряду (1.2) чи (1.3).
Граничні умови жорсткого затиснення обох кінців балки дають додатково ще чотири рівняння для визначення перших чотирьох коефіцієнтів ряду cm через тригонометричні коефіцієнти an
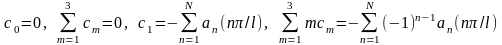 .
(1.5)
.
(1.5)
Найпростішим є рівномірне визначення точок коллокацій уздовж балки xk=kl/N, k=1,2,…N-1, хоч кращих за точністю результатів можна досягти спеціальним нерівномірним вибором точок коллокацій, застосувавши більш густу сітку точок у місцях швидкої зміни прогинів та більш рідку – у місцях повільної зміни прогинів.
Краще наближення у розрахунках коефіцієнтів дає метод Бубнова-Гальоркіна, запропонований проф. І.Г. Бубновим (1913 р.), та пізніше у більш загальній формі акад. Б.І. Гальоркіним (1915 р.). Сутність методу полягає у наступному. Підстановка наближеного розв’язку (1.2) у диференціальне рівняння (1.1) буде давати певну похибку розв’язку δ(х)
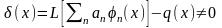 ,
(1.6)
,
(1.6)
де
для скорочення запису позначено
диференціальний оператор лівої частини
рівняння (1.1 )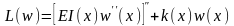 .
.
При виборі повної системи фундаментальних функцій та скінченному значенні числа членів ряду мінімум похибки δ(х) випливає з умови її ортогональності до множини фундаментальних функцій, які використано у розв’язку задачі
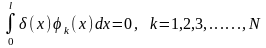 .
(1.7)
.
(1.7)
Підстановка у дану умову похибки (1.6) після інтегрування породжує наступну СЛАР

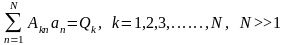 ,
(1.8)
,
(1.8)
де позначено
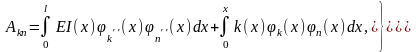 (1.9)
(1.9)
При розв’язанні задач зі складними граничними умовами знову можуть виникнути труднощі з вибором повної системи фундаментальних функцій, які б задовольняли усім граничним умовам. У таких випадках також доцільно використовувати вказану вище модифікацію даного метода [2, 5], згідно якому розв’язок диференціального рівняння (1.1) шукають у формі ряду (1.3)
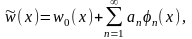 (1.10)
(1.10)
де w0(x) – додаткова функція, яка добирається так, щоб ряд (1.10) задовольняв як кінематичним, так і силовим граничним умовам на кінцях балки.
Наприклад,
у якості функції w0(x)
можна
взяти однорідний розв’язок диференціального
рівняння з постійними коефіцієнтами у
вигляді [1, 3, 4]
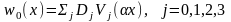 зі сталими інтегрування
зі сталими інтегрування
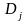 .
Далі знову повторюють процедури методу
Бубнова-Гальоркіна і отримують розширену
систему рівнянь відносно сталих Dj
та коефіцієнтів an
.
Далі знову повторюють процедури методу
Бубнова-Гальоркіна і отримують розширену
систему рівнянь відносно сталих Dj
та коефіцієнтів an
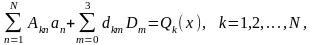 (1.11)
(1.11)
де
позначено додаткові елементи матриці
СЛАР
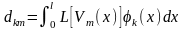 .
.
Далі
систему рівнянь (1.11) потрібно доповнити
системою чотирьох рівнянь, використавши
граничні умови на опорах балки
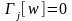 ,
,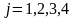 ,
де
,
де
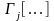 - конкретний лінійний оператор граничних
умов (наприклад, при жорсткому затисненні
маємо два оператори
- конкретний лінійний оператор граничних
умов (наприклад, при жорсткому затисненні
маємо два оператори
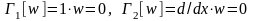 ,
а для пружної шарнірної опори з
коефіцієнтом жорсткості K
відповідно
,
а для пружної шарнірної опори з
коефіцієнтом жорсткості K
відповідно
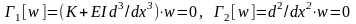 )
)
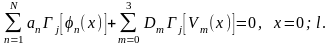 (1.12)
(1.12)
Хоч при цьому розмір спільної системи рівнянь (1.11), (1.12) і збільшився до N+4, але відпала необхідність добирати систему фундаментальних функцій φn(x) з урахуванням усіх граничних умов задачі.
Покращення збіжності рядів типу (1.2) у методі Бубнова-Гальоркіна досягається за рахунок заміни рівномірної збіжності на дискретній множині точок на інтегральну збіжність з використанням квадратур (інтегральних співвідношень) на довжині балки.
