4.2. Практичний розрахунок непризматичної одно прогонної балки на змінній пружній основі мсе

4.2.1. Розрахункова схема та вихідні дані.

З м і с т з а в д а н н я. Виконати розрахунок елементів згину заданої непризматичної балки на змінній пружній основі з пружними затисненнями на опорах за допомогою МСЕ з використанням обчислювального комплексу (пакету програм) ANSYS. Задана балка моделює згинання поздовжніх міцних фундаментних балок під головним двигуном (ГД) у машинному відділенні корпусу судна (див. рис. 1.1). Балка завантажена силами ваги ГД та силами гідростатичного тиск води на днище.

Визначити прогини, кути повороту, згинальні моменти та зрізувальні сили у наступному (безрозмірному) вигляді:

, , , .

. . . . . .

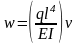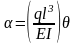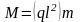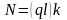Питання для самоконтролю

1. Дати загальну характеристику методу скінчених елементів (МСЕ): вказати це є точний чи наближений, аналітичний чи числовий, для яких конструкцій може застосовуватися, що підлягає дискретизації у методі.

2. Пояснити та показати на прикладі схеми дискретизації для: а) балочної б) пластинчатої та в) тривимірної розрахункових схем у МСЕ.

3. Пояснити, що таке скінченні елементи (СЕ), яких видів вони бувають для а) балочної б) пластинчатої та в) тривимірної розрахункових схем та вказати їх властивості.

4. Пояснити, чому для пластин трикутні СЕ є більш загальними ніж прямокутні СЕ.

5. Вказати, що приймається за невідомі в МСЕ: а) у варіанті методу сил та б) у варіанті методу переміщень.

6. Вказати та зобразити графічно мінімальну кількість невідомих у вузлі плоского стержневого СЕ та максимальну кількість невідомих у вузлі просторового стержневого СЕ у варіанті методу переміщень.

7. Вказати та зобразити графічно мінімальну кількість невідомих у вузлі плоского стержневого СЕ та максимальну кількість невідомих у вузлі просторового стержневого СЕ у варіанті методу сил.

8. Пояснити, як визначаються елементи згину у межах плоского балочного СЕ та який їх зв’язок з елементами згину у вузлових точках СЕ.

9. Пояснити, як визначаються елементи згину у межах плоского пластинчатого СЕ та який їх зв’язок з елементами згину у вузлових точках – вершинах СЕ.

10. Пояснити, яким чином встановлюється функціональний зав’язок між переміщеннями та зусиллями у вузлових точках скінченних елементів.

11. Вказати, які рівняння складають для визначення основних невідомих а) у варіанті методу сил та б) у варіанті методу переміщень для МСЕ.

12. Вказати, яким чинниками визначається точність розрахунків при застосування МСЕ.

5. Чисельні методи для початкових задач бмк

При розв’язанні початково-крайових задач БМК виникають початкові задачі Коші з диференціальними рівняннями за часом, наприклад, при використанні МСЕ, для інтегрування яких також було розроблено потужну множину чисельних методів [2, 6, 11]. Спільним для цих методів є дискретизація часової координати t на моменти часу t_k, k=0,1,2,… в основному з рівномірним кроком Δt (тоді t_k=kΔt), але в деяких обчислювальних схемах і з нерівномірним адаптованим кроком Δt_k (t_k=t_k-1+Δt_k). Іншим загальним положенням є те, що до моменту часу t_k розв’язок вважається відомим і потрібно його отримати для наступного моменту часу t_k+1. Різні чисельні методи як раз і відрізняються ідеями та обчислювальними алгоритмами для отримання наступного значення розв’язку при t_k+1 (рис. 5.1).

Рис. 5.1. Дискретизація часової координати

Розглянемо стисло деякі характерні та найбільш поширені приклади таких методів, розпочавши з їх класифікації. В науковій літературі [11] застосовується наступна класифікація:

1. Багато етапні чисельні методи, в яких отримання розв’язку при t_k+1 складається з декількох етапів – повторних розрахунків чи ітераційних обчислень на кожному кроці інтегрування за часом;

2. Багато крокові чисельні методи, в яких для отримання розв’язку при t_k+1 потрібно використовувати значення розв’язків для декількох попередніх моментів часу t_k, t_k-1, t_k-2,…;

3. Мінімізаційні чисельні методі, в яких для отримання розв’язку при t_k+1 використовують не вихідні диференціальні рівняння, а умови мінімуму певних функціоналів, зв’язаних з даною задачею Коші.

Менш поширеними через складність та трудомісткість є так звані блочні методи, у яких відразу розраховуються блок значень розв’язків у точках t_k, t_k+1, t_k+2,…, t_k+s; та гібридні методи, як поєднання в одному алгоритмі складових різних методів.

Типовим диференціальним рівнянням в задачах Коші для механіки і БМК зокрема є наступне диференціальне рівняння другого порядку

, (5.1)

де u(t) – динамічне переміщення, M – маса динамічної системи, Λ – коефіцієнт демпфірування, K – коефіцієнт жорсткості пружного зв’язку і f(t) – задана збуджуюча сила.

Такі диференціальні рівняння можуть утворювати й системи рівнянь відносно вектора динамічних переміщень 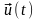з матричними коефіцієнтами M, Λ, K та вектором збуджуючих сил 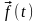, зокрема при застосування МСЕ чи МСР до динамічних задач для пружних конструкцій.

Початкові умови на переміщення та швидкість динамічної системи формулюються при t=t₀ як u(t₀)=u₀, du/dt(t₀)=v₀. Часто у якості t₀ приймають значення t₀=0.

З іншого погляду, в обчислювальній математиці використовують дещо іншу загальну форму запису диференціальних рівнянь, зокрема для рівнянь другого порядку маємо [11, 14]

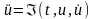, (5.2)

де у зв’язку з диференціальним рівнянням (5.1) права частина запишеться як .

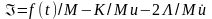Рівняння (5.2) можна про інтегрувати два рази на інтервалі [t_k, t_k+1], застосувавши метод інтегрування частинами, так що отримаємо два еквівалентні інтегральні рівняння виду

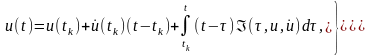(5.3)

де, нагадаємо, розв’язок при t_k вважається відомим.

Розпочнемо огляд чисельних методів з найбільш простого та прозорого методу, запропонованому ще Л. Ейлером . Згідно даному методу значення розв’язку u(t_k+1)=u_k+1 визначається за допомогою відрізку ряду Тейлора (див. рис. 5.2)

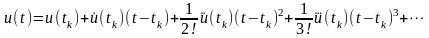. (5.4)

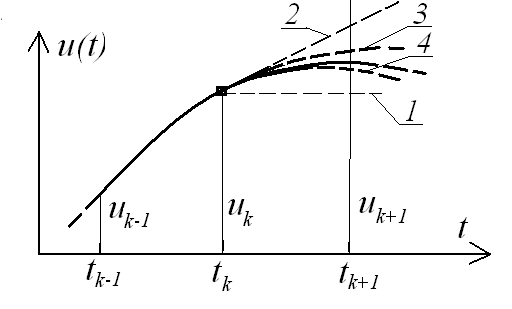
Рис. 5.2. Графічне зображення апроксимації розв’язку відрізками ряду Тейлора (цифрами показано кількість членів ряду (5.4))

Рівняння (5.2) визначає тільки другу похідну від шуканого розв’язку, але якщо функція аналітична і достатньо проста, то можна операціями інтегрування та диференціювання отримати й інші похідні у ряді (5.4) і, таким чином, отримати достатньо хороше наближення для розв’язку у точці t_k+1. Нажаль, у більшості практичних задач функція є складною, або взагалі її явний вигляд невідомий і вона розраховується тільки із застосуванням чисельних процедур, і це суттєво обмежує можливості широкого застосування метода Ейлера у практиці чисельних розрахунків задач Коші. Через це, а також через потреби досягнення якомога вищої точності, стійкості та ефективності обчислювальних алгоритмів і було розроблено потужний арсенал чисельних методів для задач Коші [11, 14].

Звернемося тепер до багато етапних методів і розглянемо два представники з даної множини методів – метод Неймарка і метод Рунге-Кутта. Для цього у ряді (5.4) утримаємо тільки перші три члени і перепишемо його в узагальненому вигляді

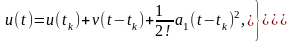(5.5)

де v, a₁ та a₂ – певні коефіцієнти ряду, різні для різних методів.

У методі Неймарка для коефіцієнта швидкості v приймається значення , а коефіцієнти прискорень a₁ та a₂ визначаються як лінійні інтерполяції для значень 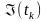та 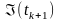. Таким чином, маємо розрахункові залежності

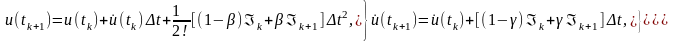(5.6)

де інтерполяційні множники β та γ загалом є довільними. В практиці розрахунків конкретних задач їх потрібно підбирати тестовими розрахунками, але досить часто беруть значення β=γ=1/2.

Як видно з формул (5.6), метод Неймарка можна реалізувати тільки у схемі повторних рекурентних розрахунків, оскільки значення переміщень, швидкостей та прискорень при t_k+1 стоять як у лівій, так і у правій частині розрахункових формул і на першому етапі вони невідомі. Тому спочатку у правій частині формул у (5.6) значення приймають наближено тільки для точки t_k, отримують їх першу оцінку для t_k+1 за даними формулами, яку потім підставляють у праву частину формул (5.6) і далі уточнюють оцінку повторними ітераційними процедурами. Якщо процес збігається, то повторні розрахунки припиняють і переходять до наступного моменту часу t_k+2. Через рекурентні обчислення на кожному кроці за часом його й відносять до багато етапних методів.

Метод Неймарка через свою простоту та прозорість досить широко використовують у практиці чисельних розрахунків задач Коші і він загалом показав достатню точність, стійкість та ефективність при обчисленнях. Крім того, його можна використовувати від першого кроку за часом, маючи тільки початкові значення u₀, v₀. Недоліком методу слід вважати невизначеність вагових множників та значний обсяг обчислень при повільній збіжності результатів рекурентних розрахунків.

Іншим широко відомим представником даної множини методів є метод Рунге-Кутта. Метод побудовано на тому, що коефіцієнти ряду (5.5) розраховують із використанням значень розв’язку як у точках t_k та t_k+1, таку і у деякій проміжній точці на інтервалі [t_k; t_k+1], зокрема при t_k+1/2=t_k+Δt/2. Такий алгоритм виник через те, що ще на початку 20-го століття спочатку Рунге та потім незалежно Кутта спробували визначити невідому першу похідну у ряді Тейлора (5.4) через відому другу похідну (згідно рівняння (5.2)) з використанням певних вагових множників та проміжних точок за часом на інтервалі [t_k; t_k+1]. Тобто 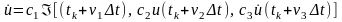, де с_j є вагові множники, а (t_k+v_jΔt) (v_j<1, в основному v_j=1/2) є проміжні точки за часом. Оскільки підбір даних множників можна виконувати різними способами, то існує низка варіантів даного методу і, як приклад, наведемо 4-х етапний метод у вигляді [14]

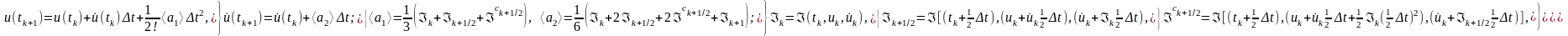, ( 5.7)

де верхнім індексом «с» позначено скориговане значення для .

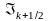Як і метод Неймарка, даний метод також може «стартувати» з початкових умов, має високі показники стійкості та точності і досить широко використовується у практиці розрахунків, а недоліком методу слід вважати великий обсяг обчислень на кожному кроці за часом у задачах зі складними та трудостісткими алгоритмами для обчислень правої частини диференціальних рівнянь типу (5.2) (наприклад, у задачі про нелінійну хитавицю суден).

Р озглянемо далі багато крокові методи, зокрема сімейство чисельних методів Адамса, у яких використовується інтегральна версія вихідних диференціальних рівнянь типу (5.3). Ідея методу полягає у тому, що для розрахунку інтегралів у (5.3) підінтегральні вирази апроксимуються інтерполяційними поліномами «назад» для певної множини точок за часом t_k, t_k-1, t_k-2,…, t_k-s, s=1,2,3… . Може бути задіяна для інтерполяції і точка t_k+1, але тоді, як і у методі Неймарка, потрібно застосовувати додатково рекурентні розрахунки, оскільки невідомі розв’язки при t_k+1 будуть як у лівій, так і у правій частині розрахункових формул. Наприклад, при лінійній інтерполяції для точок t_k, t_k-1 маємо 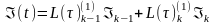, де 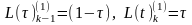, , 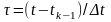а при квадратичній інтерполяції для точок t_k, t_k-1, t_k-2 відповідно 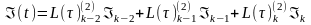, де вже інтерполяційні поліноми мають вигляд 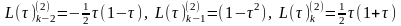з тим же виразом для τ (рис. 5.3). Степеневі функції легко інтегруються і тоді інтегральні рівняння в (5.3) перетворюються в алгебраїчні відносно вузлових значень шуканих розв’язків. Тут також можна отримати різні варіанти методів, зокрема, якщо точка за часом t_k+1 не використовується, то утворюються так звані явні схеми Адамса-Бешфорта, а якщо в інтерполяцію включено і точку t_k+1, то матимемо більш складні неявні схеми Адамса-Мултона [11].

Рис. 5.3. Схеми інтерполяції (- - - - ) у методах Адамса; а) лінійна, б) квадратична інтерполяція

У якості приклада наведемо розрахункові формули для явної схеми з назвою «предиктор-коректор» [11]

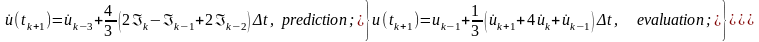. (5.8)

Як видно з розрахункових формул, у даному методі розрахунок виконується відразу за один етап, але при цьому потрібно мати розрахунки у попередніх точках за часом t_k, t_k-1, t_k-2, t_k-3 і це означає, що методи Адамса не можна використовувати, починаючи з граничних умов задачі. Тому при практичних застосуваннях даних методів спочатку для перших кроків за часом виконують розрахунки одним з багато етапних методів, а потім вже переходять на використання методів Адамса. Позитивною стороною даних методів є відносно менший обсяг розрахунків на кожному кроці, а негативною – неможливість застосування, починаючи відразу з граничних умов задачі.

Розглянемо нарешті мінімізаційні чисельні методи для задач Коші на прикладі методу Куявського-Галагера як узагальненого варіанту методу найменших квадратів. У даному методі, як і у методах Адамса, розв’язок інтерполюється поліномами другого прядку на інтервалі [t_k-1; t_k+1] 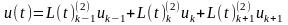. Таким же чином інтерполюється і збуджуюча сила f(t).

Підстановка даного виразу у диференціальне рівняння (5.1) утворює похибку

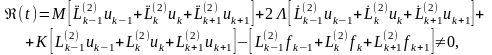(5.9)

для якої визначається функціонал – сумарний квадрат похибки розв’язку на інтервалі [t_k-1; t_k+1]

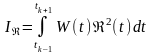. (5.10)

де W(t) – певна вагова функція, яка підбирається з умов точності та стійкості обчислювальної схеми.

Оскільки найкращий розв’язок забезпечується умовами мінімуму даного функціоналу, то шукане значення u_k+1 визначається формулою

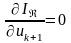. (5.11)

Остаточно після необхідних математичних дій може бути отримана наступна обчислювальна схема

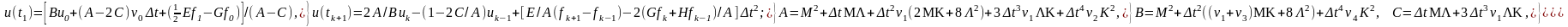(5.12)

де 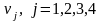- вагові коефіцієнти, які дорівнюють 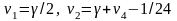, 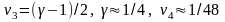(визначені з умов точності четвертого порядку за кроком Δt та безумовної стійкості обчислювальної схеми).

Практичне застосування даного алгоритму у задачах нелінійної хитавиці суден на хвилях показало високий рівень стійкості результатів навіть при малому числі кроків за період коливань (порядку 10–15). Метод також можна застосовувати, починаючи з граничних умов задачі, але недоліком методу є відносно великий обсяг обчислень на кожному кроці за часом для задач зі складними алгоритмами розрахунків для коефіцієнтів та правої частини диференціальних рівнянь задачі.

На завершення на рис (5.4) – (5.6) наведено приклади чисельного інтегрування диференціального рівняння 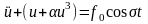(нелінійний осцилятор при α≠0) методами Неймарка, Рунге-Кутта, Адамса-Бешфорта та мінімізаційним методом Куявського-Галагера. Крок за часом становив 1/10 від періоду власних коливань осцилятора.

Рис. 5.4. Вільні коливання лінійного осцилятора (при u₀=1, v₀=0, α=0, f₀=0); метод Неймарка ( - - - - ), метод Рунге-Кутта (x—x), метод Адамса-Бешфорта (+—+), метод Куявського-Галагера (▲—▲), точний розв’язок (——)

Я к видно з графіків коливань, після 50-го кроку за часом у розв’язку за методом Неймарка сформувався помітний фазовий зсув, а у розв’язку за методом Адамса-Бешфорта почала формуватися нестійкість за амплітудами коливань осцилятора. Інші чисельні розв’язки добре узгоджуються з точним розв’язком.

Рис. 5.5. Вимушені коливання лінійного осцилятора (при u₀=0, v₀=0, α=0); метод Неймарка ( - - - - ), метод Рунге-Кутта (x—x), метод Адамса-Бешфорта (+—+), метод Куявського-Галагера (▲—▲), точний розв’язок (——)

Д ля даного варіанту розрахунків з графіків коливань видно, що після 50-го кроку за часом у розв’язку за методом Неймарка сформувалася помітна нестійкість за амплітудами коливань та фазовий зсув, а усі інші чисельні розв’язки досить добре узгоджуються з точним розв’язком. Відхилення за амплітудами у методі Адамса-Бешфорта ледь помітні на даному інтервалі за часом.

Рис. 5.6. Вимушені коливання нелінійного осцилятора (при u₀=1, v₀=0,); метод Неймарка (- - -), метод Рунге-Кутта (x—x), метод Адамса-Бешфорта (+—+), метод Куявського-Галагера (▲—▲), аналітичний розв’язок (——)

Для нелінійних вимушених коливань осцилятора при застосуванні метода Адамса-Бешфорта сильна амплітудно-фазова нестійкість розпочалася вже після 10-го кроку за часом і така ж нестійкість почала формуватися при застосуванні метода Неймарка. Після 50-го кроку для решти двох методів маємо, що для метода Рунге-Кутта виник невеликий стабільний зсув за фазою, а метод Куявського-Галагера дав практично точне узгодження з аналітичним розв’язком.

Таким чином, майже кожний з використаних методів починає з певного кроку за часом накопичувати більші чи менші похибки у розв’язках у вигляді зсуву фази коливань чи розгойдування амплітуд (амплітудної нестійкості) і загалом це є типовим явищем для чисельних методів у задачах Коші. Швидке накопичення похибок чисельних розв’язків у наведених прикладах пов’язане у першу чергу із спеціально вибраним досить великим кроком за часом; в реальних розрахунках звичайно крок беруть значно меншим, щоб нестійкості з’являлися якомога пізніше. Тому і чисельних методів для задач Коші було розроблено достатньо багато з метою подолання проблем точності, нестійкості та обчислювальної ефективності для конкретних типів задач.