4. Розрахунок згину суднових балок методом скінченних елементів

4.1. Теоретичні положення методу скінченних елементів у бмк

Розглянутий у попередньому розділі МСР зустрічає певні труднощі при застосуванні його до розгалужених стержневих розрахункових схем – багато прогонних балок, рам, перекриттів, пластинчатих конструкцій зі складною топологією взаємного розташування тощо. Тому у будівельній механіці корабля було розроблено значно більш ефективний, потужний та універсальний метод – метод скінченних елементів (МСЕ). На відміну від МСР, у якому дискретизації підлягає координатна область, яку займає конструкція, МСЕ ґрунтується на дискретизації безпосередньо розрахункової схеми конструкції на окремі елементи відносно малого розміру – скінченні елементи.

МСЕ було розроблено у 60-ті роки минулого століття та після залучення ЕОМ у практику інженерних розрахунків у 70-ті роки він знайшов широкого застосування у розрахунках міцності та при проектуванні суднових конструкцій. На даний час МСЕ настільки узагальнено та удосконалено, що даним методом розраховують як міцність корпусу в цілому (рис. 4.1,а), так і окремі його відсіки (рис. 4.1,б). На даний час МАКО взагалі вимагає обов’язкового розрахунку міцності трьох відсіків корпусу за МСЕ для нових проектів суден.

а) б)

Рис. 4.1. Представлення корпусу судна та його відсіків у МСЕ

Розглянемо стисло теоретичні основи методу скінченних елементів для того, щоб студенти розуміли сутність методу при практичному використанні стандартних програм МСЕ. У першу чергу підкреслимо ще раз, що МСЕ цілковито зорієнтований на застосування обчислювальної техніки, оскільки остаточно призводить до систем лінійних алгебраїчних рівнянь (СЛАР) високого та дуже високого порядку (10³–10⁶), які неможливо розв’язати без застосування ЕОМ. Але, з іншого боку, застосування МСЕ дозволяє враховувати складність та просторовий характер геометрії розрахункової схеми конструкції, не призматичність та нерегулярність розташування її елементів, локальні підкріплення, реальні умови закріплень та взаємодії із суміжними конструкціями тощо. Його практична ефективність на даний час забезпечується достатньо великою кількістю обчислювальних комп’ютерних комплексів, розроблених за останні два десятиліття активного напрацювання технології МСЕ (ANSYS, Solid Works, тощо). При цьому, якщо перші версії програм з МСЕ могли опрацьовувати сотні чи тисячі скінченних елементів при ручному способі дискретизації розрахункової схеми, то сучасні потужні обчислювальні комплекси дають змогу працювати з тривимірними розрахунковими схемами, які можуть містити від сотень тисяч до мільйонів скінченних елементів з дискретизацією у автоматизованому режимі.

4.1.1. МСЕ при стержневій дискретизації конструкції

З методичної точки зору простіше розглянути основи МСЕ при стержневій дискретизації розрахункової схеми конструкції. Тому спочатку більш детально розглянемо даний варіант МСЕ а на завершення стисло викладемо більш загальний варіант МСЕ при пластинчатій дискретизації, яка також добре відповідає тонкостінним корабельним конструкціям.

У будь якому варіанті МСЕ містить певну послідовність процедур, які у сукупності і становлять його сутність. Розв’язок задачі у МСЕ починають з розділення розрахункової схеми пружного тіла чи конструкції на певну сукупність малих частин – скінченних елементів. Як вже було зазначено, СЕ можуть бути одновимірними (стержневими) уздовж осей стержнів у складі стержневих систем, двовимірними (пластинчатими – трикутними чи чотирикутними) для пластин і оболонок, нарешті тривимірними (просторовими) у вигляді тетраедрів або паралелепіпедів для пружних тіл довільної форми. Важливим є те, що геометричні, жорсткістні і силові характеристики СЕ повинні бути відносно простими – їм повинна бути властива зокрема прямолінійність, призматичність, рівномірність навантаження тощо.

Скінченні елементи та вузли нумерують відповідним чином і для складних розрахункових схем формують спеціальну матрицю індексів, пов’язаних з прийнятою нумерацією. Загалом для складних розгалужених чи тривимірних розрахункових схем процедура нумерації є досить складною і тому намагаються її автоматизувати. На рис. 4.2 наведено приклад дискретизації простої одно прогонної бали.

Рис. 4.2. Дискретизація одно прогонної балки у МСЕ

Приймається, що елементи взаємодіють між собою у скінченному числі вузлових точок, де суміжні СЕ з’єднуються між собою (у вузлах з’єднання стержневих СЕ, у вершинах плоских чи просторових СЕ). До розгляду вводяться кутові та поступальні переміщення даних вузлів та внутрішні зусилля взаємодії СЕ. При цьому, якщо за основні невідомі, для яких буде отримано остаточні рівняння, приймають вузлові переміщення, то даний варіант МСЕ належить до множини методів переміщень, а якщо за основні невідомі приймають внутрішні зусилля у вузлах, то отримаємо варіант методу сил. Більшого поширення знайшов варіант методу переміщень, зокрема через те, що розрахунки для переміщень простіше аналізувати, а також тому, що рівняння рівноваги у вузлах для першого варіанту МСЕ складати простіше, ніж рівняння сумісності переміщень для другого варіанту МСЕ. На рис. 4.3 наведено приклад визначення вузлових зусиль у стержневому СЕ при плоскому згині балки від дії поперечних навантажень.

Рис. 4.3. Вузлові зусилля для стержневого СЕ

Вузлові зусилля у даному випадку – це зрізувальні сили та згинальні моменти на кінцях СЕ, які зручно позначати уніфіковано як Q_j , j=1,2,3,4 і які на рис. 4.3 вказано додатними. Зрозуміло, що Q₁, Q₃ – це зрізуючі сили, а Q₂, Q₄ – згинальні моменти на кінцях СЕ. Вузлові переміщення – прогини та кути повороту кінцевих перерізів СЕ також позначають уніфіковано як u_j , j=1,2,3,4 і їх додатні напрямки відповідають напрямкам вузлових зусиль на рис. 4.3. Відповідно переміщення u₁, u₃ є прогини у вузлах, а u₂, u₄ – кути повороту поперечних перерізів у вузлах СЕ (див. також нижче рис. 4.4). Із загального погляду у термінах узагальнених сил та переміщень механіки деформівного тіла величини Q_j є узагальнені сили, а величини u_j – узгоджені з ними узагальнені переміщення для даного СЕ.

У загальному випадку тривимірної багато стержневої системи її скінченні елементи можуть зазнавати усі види деформацій – поздовжні (розтягування-стискання), кручення, косе згинання, і тому для кожного кінця СЕ потрібно задавати шість зусиль Q_j , j=1,…,6 – поздовжню силу, крутний момент та по два значення зрізуючих сил та згинальних моментів у площинах головних центральних осей поперечних перерізів СЕ. Відповідно визначається і шість вузлових переміщень u_j , j=1,…,6 – поздовжні переміщення, кути кручення та прогини і кути повороту поперечних перерізів у вузлах у локальній системі координат, зв’язаній з головними центральними осями даного СЕ. Таким чином, для кожного СЕ загалом буде визначено дванадцять вузлових зусиль та дванадцять вузлових переміщень. Відмітимо для подальшого, що у навчальній та науковій літературі [2, 9] поширеним є застосування матрично-векторного способу запису величин, наприклад, 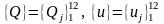і т. ін., що забезпечує компактність записів для залежностей у МСЕ.

Кожний СЕ визначається у своїй локальній системі координат, але повну розрахункову схему визначено у так званій глобальній системі координат і тому додатково потрібно визначати зв'язок між проекціями вузлових величин у обох системах координат. З курсу векторної алгебри маємо співвідношення {Q}_лок=[T]^T{Q}_глб, де =[T]^T транспонована матриця косинусів кутів взаємної орієнтації обох систем координат (детальніше це питання див. у [2, 9]).

Вузлові зусилля та вузлові переміщення визначають елементи НДС у СЕ тільки у вузлових точках і тому наступний етап у МСЕ полягає у інтерполяції переміщень між вузловими точками СЕ. У стержневих СЕ для прогинів застосовують поліноми виду w(x)=a₀+a₁x+a₂x²+a₃x³, які є розв’язком рівняння згину СЕ EIw^IV=0. Коефіцієнти a_j, j=0,1,2,3 шукають, порівнявши прогини w(x) та кути повороту α(x)=dw(x)/dx з їх вузловими значеннями: w(0)=u₁, α(0)=u₂, w(a)=u₃, α(a)=u₄.

Рис. 4.4. Вузлові переміщення та інтерполяція прогинів між вузлами

Остаточно результат записують із застосуванням ортогональних поліномів Ерміта H_j(x) [2, 9]

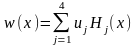, (4.1)

де H₁=1–3ξ²+2ξ³, H₂=ξ–2ξ²+ξ³, H₃=3ξ²–2ξ³, і H₄=–ξ²+ξ³, ξ=a/x≤1. Взаємна ортогональність поліномів Ерміта дає змогу спростити результати при подальших математичних перетвореннях в методі.

Вузлові зусилля Q_j та вузлові переміщення u_j зв’язані між собою і для отримання відповідних формул використовують теорему Лагранжа (з урахуванням дії зовнішніх сил), Q_j=∂(V–U)/∂u_j, де V – потенціальна енергія деформування СЕ, а U – робота зовнішніх навантажень на СЕ [1, 2]. Для стержневого елемента, який працює тільки на згинання при дії поперечного навантаження, маємо

. (4.2)

Якщо розглядати більш загальний варіант СЕ з урахуванням пружної основи та деформацій зсуву, то у формулу (4.2) потрібно додати відповідні потенціальні енергії деформацій зсуву та пружної основи

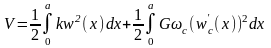. (4.3)

Підстановка у дані інтеграли апроксимацій типу (4.1) та визначення похідних за вузловими переміщеннями остаточно призводить до залежності між вузловими зусиллями та вузловими переміщеннями при дії поперечних навантажень на СЕ. У векторно-матричній формі запису маємо [2, 6]:

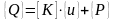, (4.4)

де {Q} – вектор вузлових зусиль (вектор-стовпець з елементів Q_j); {u} – аналогічний вектор вузлових переміщень СЕ; {P} – вектор зовнішніх вузлових зусиль – так званий «вантажний» вектор, який фактично представляє реакції від дії зовнішніх навантажень на СЕ при умові жорсткого закріплення у вузлах СЕ (тобто при умові що вектор {u}=0); [K] – квадратна матриця жорсткості СЕ розміром (4×4) для плоского згину і (12×12) у загальному випадку з відомими елементами k_ij [2, 9]. При додатковому врахуванні пружної основи та деформацій зсуву матриця жорсткості при плоскому згині буде мати вигляд [2, 9]

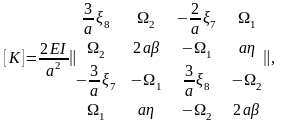(4.5)

де винесено спільний множник 2EI/a² і множники, що враховують пружну основу та деформації зсуву при наближеному незалежному їх врахуванні мають вигляд [2, 9]

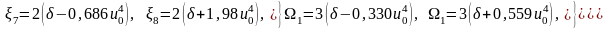(4.6)

де також позначено .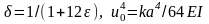

Вектор-стовпчик зовнішніх вузлових сил при дії рівномірного навантаження на СЕ має вигляд {P_j}={– qa/2; – qa²/12; – qa/2; qa²/12}^T.

Останній етап у МСЕ пов'язаний із складанням рівнянь рівноваги зусиль у кожному вузлі розрахункової схеми і для зображеної на рис. 4.1 схеми балки такі рівняння мають вигляд (див. рис. 4.5)

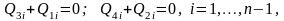(4.7)

де другий індекс і зусиль відповідає номеру вузла, а перший індекс – номеру самого зусилля у визначеному вище типі СЕ (див. рис. 4.3). Обов’язково враховують також граничні умови на кінцях балки.

Рис. 4.5. Вузлові зусилля у довільному і-му вузлі

Підставивши у рівняння (7.4) залежності для вузлових зусиль, остаточно отримують повну (глобальну) систему рівнянь для вузлових переміщень усієї розрахункової схеми конструкції; розв’язок якої дає чисельні значення для вузлових переміщень. Далі за відповідними формулами розраховуються вузлові зусилля, деформації та напруження.

Зазначимо, що точність розрахунків задач міцності за даним методом пов’язана як з використанням дискретної моделі замість неперервної розрахункової схеми конструкції, так і з округленням чисел та математичними операціями у процесі розрахунків на ЕОМ. Помилка дискретизації зменшується зі зменшенням розміру елемента, тобто зі збільшенням числа СЕ. У той же час при зменшенні розмірів СЕ починають збільшуватися обчислювальні похибки округлення чисел та через великий обсяг математичних операцій і тому існує певний оптимальний варіант дискретизації, що відповідає мінімальній сумарній похибці розрахунків за МСЕ.

4.1.2. МСЕ при пластинчатій дискретизації конструкції

Більш загальним варіантом дискретизації тонкостінних суднових конструкцій є пластинчата дискретизація із СЕ у вигляді чотирикутних чи трикутних пластинок (рис. 4.6). Прямокутні скінченні елементи є найбільш простими, але вони мало придатні для пластин з вирізами, пластин з не ортогональними чи криволінійними сторонами тощо. У таких випадках більш ефективними виявляються трикутні СЕ з довільним розташуванням вершин трикутників. Тому далі розглянемо тільки трикутні СЕ на прикладі плоскої задачі теорії пружності для тонких суднових пластин [1, 2].

Рис. 4.6. Дискретизація пластини з вирізом прямокутними та трикутними СЕ

У плоскій задачі теорії пружності, сформульованій у переміщеннях, основними є диференціальні рівняння Ламе у частинних похідних для переміщень u(x,y), v(x,y) у площині пластини

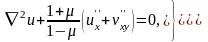(4.8)

із заданими кінематичними чи силовими граничними умовами на сторонах пластини.

При пластинчатій дискретизації пружної конструкції із використанням трикутних СЕ за невідомі приймають переміщення у вершинах трикутних СЕ (на рис. 4.7 показано переміщення у вузлах плоского пластинчатого СЕ).

Рис. 4.7. Переміщення у вузлах трикутного СЕ

Для інтерполяції поля переміщень у локальній системі координат Oxy у межах СЕ можуть бути використані лінійні поліноми типу u(x,y)=a₀+a₁x+a₂y, v(x,y)=b₀+b₁x+b₂y, оскільки диференціальні рівняння (4.7) є рівнянням другого порядку. Коефіцієнти поліномів a_j та b_j також шукають з умови рівності апроксимацій вузловим переміщенням у вершинах трикутного СЕ (рис. 4.8), що остаточно дає залежності 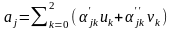, , 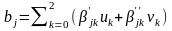де α'_jk , α''_jk та β'_jk , β''_jk є певні чисельні коефіцієнти [2, 9].

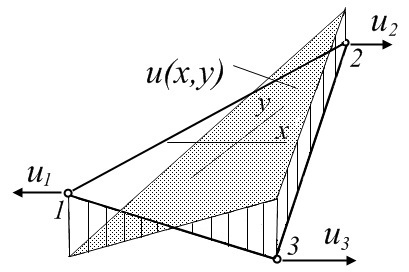
Рис. 4.8. Інтерполяція переміщення u(x,y) у межах трикутного СЕ

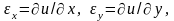
Залежності для деформацій та напружень у вузлах СЕ отримують наступним чином. Спочатку у рівняння Коші 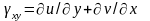підставляють записані вище апроксимації для переміщень, що дає змогу отримати співвідношення {ε}=[D]{u}, де {ε}={ε_x, ε_y, γ_xy}^T – постійний у межах СЕ локальний вектор-стовпчик деформацій,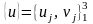 – повний локальний вектор вузлових переміщень та [D] – прямокутна (3×6) матриця зв’язку між вузловими деформаціями та переміщеннями. Далі отримані таким чином деформації підставляють у рівняння узагальненого закону Гука 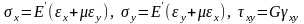, де E’=E/(1–μ²), G=E/2(1+μ), що дає змогу отримати остаточно аналогічне співвідношення {σ}=[ E_σ]{u}, де { σ }={ σ _x, σ _y, τ_xy}^T – постійний у межах СЕ локальний вектор-стовпчик напружень і [E_σ] – прямокутна (3×6) матриця зв’язку між вузловими напруженнями та переміщеннями у СЕ. Матриці [D] та [E_σ] можна знайти у підручнику [2].

При лінійному законі інтерполяції поля переміщень у межах СЕ поля деформацій та напружень виявилися локально постійними у межах СЕ (рис. 4.9) та глобально кусково-постійними для усієї пластини із розривами першого роду (стрибками) на границях між сусідніми СЕ. Для отримання неперервних полів деформацій та напружень потрібно застосовувати принаймні квадратичну інтерполяцію поля переміщень, але це потребує введення до розгляду додаткових проміжних точок на сторонах чи по полю трикутного СЕ.

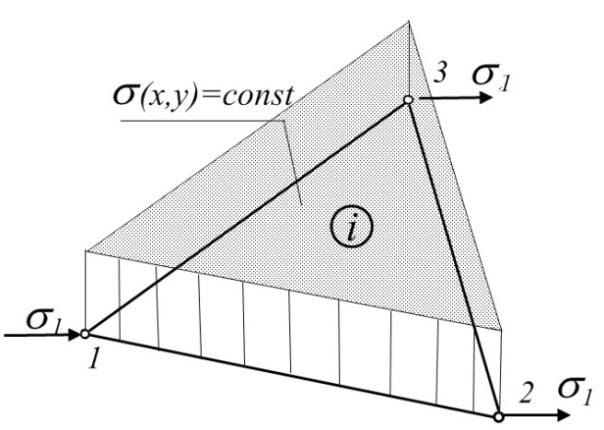
Рис. 4.9. Постійне поле напружень у межах трикутного СЕ

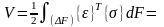
Отримані залежності для деформацій та напружень підставляють у потенціальну енергію пружних деформацій СЕ у своїй площині 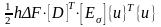, де h і ∆F – товщина та площа СЕ. Застосування теореми Лагранжа Q_j=∂V/∂u_j остаточно дає для матриці жорсткості трикутного СЕ у залежності {Q}=[K]{u} наступний вираз [K]=h∆F[D]^T [E_σ].

Нарешті, для кожного вузла складають рівняння рівноваги узагальнених зусиль у проекціях на декартові осі координат, наприклад, ∑_kQ_ik=0 для і-го вузла, які у сукупності та з урахуванням граничних умов утворюють повну систему рівнянь у МСЕ для плоскої задачі.

Рис. 4.10. Узагальнені зусилля у і-му вузлі для трикутних СЕ