На диаграмме обозначены продольная и поперечная составляющие падения напряжения в линии U = U’ + jU’’.

Из диаграммы на рис. 2.7 следовало, что величина падения напряжения является характеристикой загрузки ЛЭП: |U| – пропорциональна току нагрузки. Другой характеристикой режима работы ЛЭП является потеря напряжения, которая вычисляется как разность модулей напряжений по концам линии U = U₁ – U₂ и в отличие от падения напряжения, которое есть векторная величина, является скалярной величиной.

На векторной диаграмме (рис. 2.8) потерю напряжения можно получить как разность отрезков U₁ и U₂. На вещественной оси отмечен отрезок, равный по величине U₁, полученный с помощью проведения дуги соответствующего радиуса, и отрезок, равный потере напряжения U.

Особое значение для характеристики загрузки линии потеря напряжения имеет для линий, у которых R и X близки друг к другу или R > X, тогда потерю напряжения приближенно можно принять равной продольной составляющей падения напряжения . Это относится к линиям низкого и среднего напряжения, которые выполняются проводами сечением 70 мм² (для АС 70/11: r₀ = 0,428 Ом/км, x₀ = 0,432 Ом/км на 35 кВ) и менее и с меньшими междуфазными расстояниями, чем на высоком напряжении.

2.5. Натуральная мощность и пропускная способность лэп Натуральная мощность

Рассмотрим ЛЭП без потерь, для которой r₀ = 0 и g₀ = 0.

Выделим в ней отрезок единичной длины l с индуктивным сопротивлением x₀l и емкостной проводимостью b₀l. На этом участке имеют место потери и генерация реактивной мощности

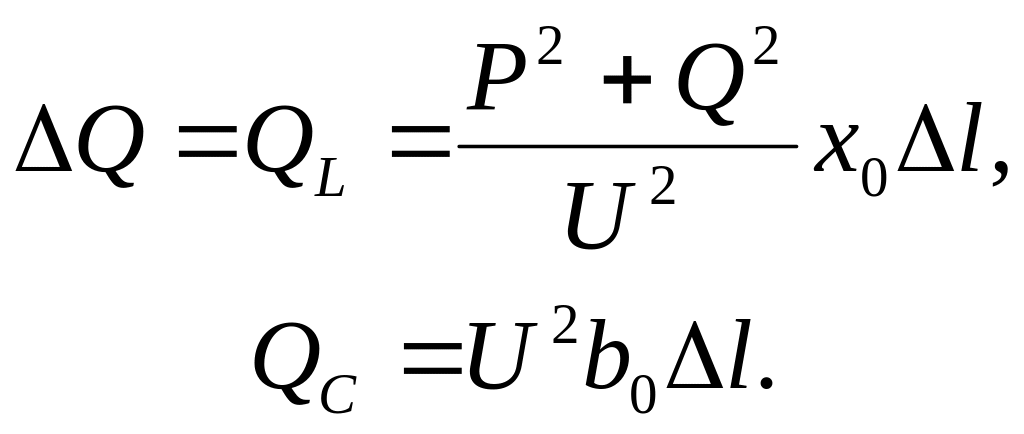(2.39)

Здесь Q_C не зависит от передаваемой мощности. Если принять Q = 0, то при некоторой активной мощности P будет иметь место равенство Q_L = Q_C. Мощность, передаваемую в этом режиме называют натуральной мощностью P_нат, а сам режим работы ЛЭП называют режимом передачи натуральной мощности. При U = U_ном будем иметь

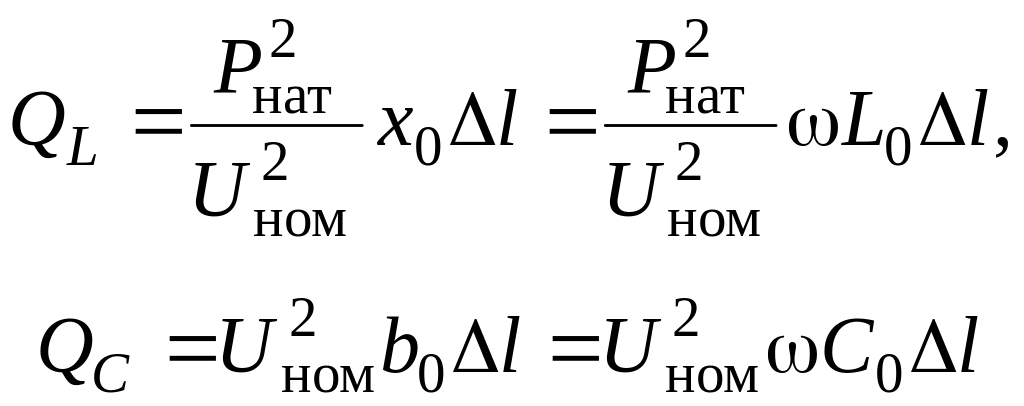(2.40)

и

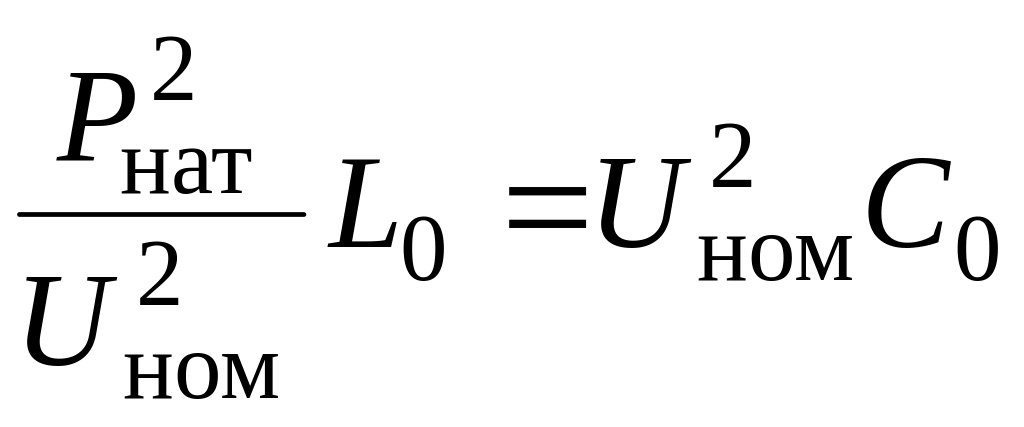, (2.41)

откуда

(2.42)

или

(2.43)

где – волновое сопротивление линии.

В реальной линии, в которой r₀  0 g₀  0, потери активной мощности при Q = 0 будут наименьшими

(2.44)

а при P = P_нат линия будет работать с наибольшим КПД вследствие того, что линия находится на самобалансе реактивной мощности Q_L = Q_C – потери в линии компенсируются зарядной мощностью и в любой точке линии Q = 0. В случае, когда Q_L  Q_C имеет место либо избыток зарядной мощности Q_C > Q_L, либо потери превышают зарядную мощность Q_L > Q_C, и тогда потери P увеличиваются и вследствие этого КПД линии ухудшается, как при P > P_нат, так и при P < P_нат.

Режим натуральной мощности является не только самым экономичным. Для линии без потерь можно обнаружить и другие его замечательные свойства, так, например, напряжение в начале линии по модулю оказывается равным напряжению в конце линии:

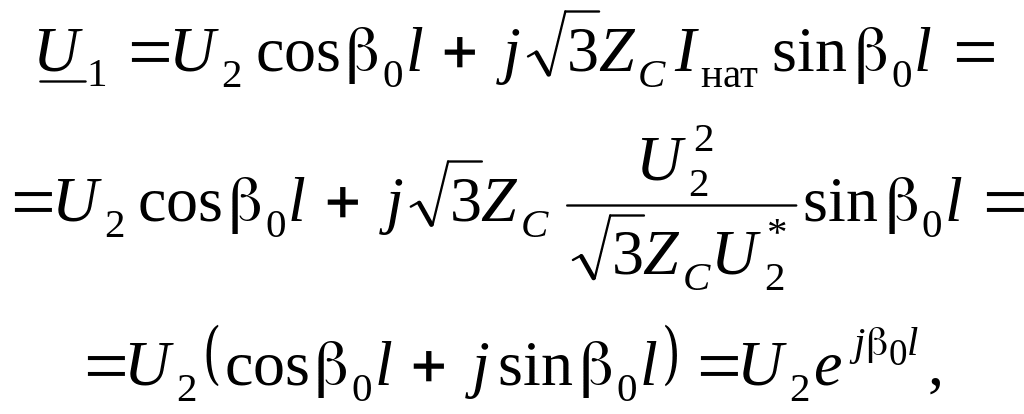(2.45)

где ; Z_C – волновое сопротивление линии; ₀ – коэффициент фазы линии, а U₂ – совмещено с действительной осью координат.

Из соотношения следует, что равны по модулю не только напряжения по концам линии, но и то, что модуль напряжения в любой точке вдоль линии является неизменной величиной: , где x – расстояние от начала линии (x = 0) до точки с координатой x. Можно показать, что для линии без потерь в режиме натуральной мощности и ток вдоль линии по модулю остается постоянной величиной.

Такое свойство постоянства напряжения и тока вдоль линии в режиме натуральной мощности во многом снижает требования к оборудованию линии электропередачи и облегчает регулирование режимов ЭЭС.

Наличие активных параметров линии r₀ и g₀ несколько меняет идеальную картину, но при P₂ = P_нат или P₂ , близкой к натуральной, в линии приблизительно сохраняются свойства режима натуральной мощности.

В табл. 2.1 приведены численные значения натуральной мощности ВЛ некоторых напряжений. Натуральные мощности кабельных линий на порядок выше, чем у ВЛ.

Т а б л и ц а 2.1

Величины натуральной и наибольшей передаваемой мощности вл

Мощность	Номинальное напряжение, кВ
	110	220	500
Натуральная	30	120	900
Наибольшая*	20…50	90…200	700…900

* Наибольшая мощность зависит от длины линии.

На практике невозможно обеспечить работу всех линий в режиме, близком к натуральному, но этого добиваются для отдельных линий, когда существует возможность регулировать передаваемую мощность за счет перераспределения мощностей в электрической сети и генерирования реактивной мощности в местах ее потребления.