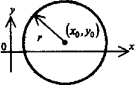1.2. Способы задания функций

Задать функцию означает установить правило (закон), с помощью которого по данным значениям независимой переменной следует находить соответствующие им значения функции. Рассмотрим некоторые способы задания функций.

Табличный способ. Довольно распространенный, заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством.

Преимущества табличного способа задания функции состоят в том, что он дает возможность определить те или другие конкретные значения сразу, без дополнительных измерений или вычислений. Однако, в некоторых случаях таблица определяет функцию не полностью, а лишь для некоторых значений аргумента и не дает наглядного изображения характера изменения функции в зависимости от изменения аргумента.

	0	1	-1	2	-2
	0	1	1	4	4

Например:

Графический способ. Графиком функции называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению.

Графический способ задания функции не всегда дает возможность точно определить численные значения аргумента. Однако он имеет большое преимущество перед другими способами - наглядность. В технике и физике часто пользуются графическим способом задания функции, причем график бывает единственно доступным для этого способом. Например,

Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим. Например: .

Этот способ дает возможность по каждому численному значению аргумента найти соответствующее ему численное значение функции точно или с некоторой точностью.

Аналитический способ является самым распространенным способом задания функций. Компактность, лаконичность, возможность вычисления значения функции при произвольном значении аргумента из области определения, возможность применения к данной функции аппарата математического анализа — основные преимущества аналитического способа задания функции. К недостаткам можно отнести отсутствие наглядности, которое компенсируется возможностью построения графика и необходимость выполнения иногда очень громоздких вычислений.

1.3. Графики элементарных функцй

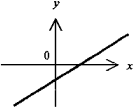
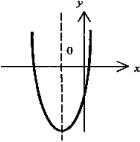
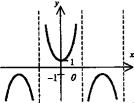
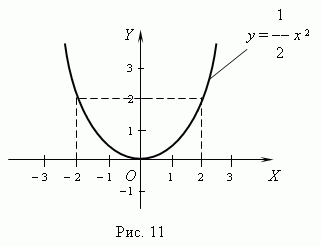
Прямая линия - график линейной функции y = ax + b. Функция y монотонно возрастает при a > 0 и убывает при a < 0. При b = 0 прямая линия проходит через начало координат т. 0 (y = ax - прямая пропорциональность) Парабола - график функции квадратного трёхчлена у = ах2 + bх + с. Имеет вертикальную ось симметрии. Если а > 0, имеет минимум, если а < 0 - максимум. 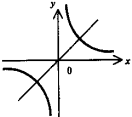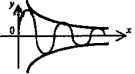Точки пересечения (если они есть) с осью абсцисс - корни соответствующего квадратного уравнения ax2 + bx +с =0 Гипербола - график функции . При а > 0 расположена в I и III четвертях, при а < 0 - во II и IV. Асимптоты - оси координат. Ось симметрии - прямая у = х(а > 0) или у - - х(а < 0). 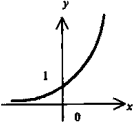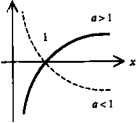Экспонента (показательная функция по основанию е) у = еx. (Другое написание у = ехр(х)). Асимптота - ось абсцисс. Логарифмическая функция y = logax (a > 0) . 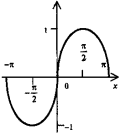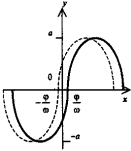Синусоида у = sinx - периодическая функция с периодом Т = 2π у = аsin(ωx+φ) - функция гармонических колебаний. Обозначения: а - амплитуда, ω - частота (ω = 2π/Т), φ - фаза (сдвиг). 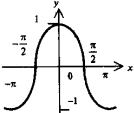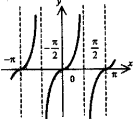Косинусоида у = cosx (графики у = sinx и у = cosx сдвинуты по оси х на ) Тангенсоида y = tgx. Точки разрыва при х = (2k -1), где k = 0, ±1, ±2,.. Вертикальные асимптоты в этих точках. у = secx - кривая "цепной линии", эту форму принимает абсолютно гибкая нить, подвешенная в параллельном поле тяжести. А полная функция периодична, и её асимптоты х = (2k -1), как у функции y = tgx. Круг с центром в точке (xo, yo) радиуса r. 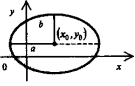(x-xo)2 + (y-yo)2 = r2 Эллипсс центром в точке (xo, yo). Большая полуось а, малая b, эксцинтриситет , Затухающее колебание y = Ae-ax•sin(ωx+φ)