2.1.Основные числовые характеристики дискретной случайной величины

Закон распределения случайной числовой величины характеризует ее полностью, но наиболее компактно можно выразить все существенные сведения о случайной величине, которыми мы располагаем, с помощью числовых параметров, получивших название числовых характеристик случайной величины, из которых рассмотрим математическое ожидание, дисперсию и среднеквадратическое отклонение.

Определение. Математическим ожиданием называется сумма произведений всех возможных значений случайной величины на вероятности этих значений

.

Математическое ожидание соответствует тому значению случайной величины, около которого группируются все ее возможные значения.

Математическое ожидание обладает следующими свойствами:

1. Математическое ожидание постоянной величины равно этой постоянной величине:

.

2. Постоянный множитель можно выносить за знак математического ожидания:

.

3. Математическое ожидание алгебраической суммы случайных величин равно алгебраической сумме их математических ожиданий:

.

4. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий:

.

5. Математическое ожидание отклонения случайной величины от ее математического ожидания всегда равно нулю:

.

Пример. Вычислить математическое ожидание дискретной случайной величины , определяемой как количество посетителей в наугад выбранной аптеке.

Х:	xi	5	6	7	8	9
	pi	0,1	0,2	0,3	0,3	0,1

Решение:

Математическое ожидание дискретной случайной величины Х определяется как сумма произведений всех возможных значений случайной величины на их вероятности:

= 50,1 +60,2 +70,3 + 80,3 + 90,1 = 7,1.

Определение. Математическое ожидание квадрата отклонения случайной величины от ее математического ожидания называется дисперсией случайной величины

.

На практике широко применяется другая формула, значительно упрощающая процесс вычисления

.

Дисперсия случайной величины обладает следующими свойствами:

1. Дисперсия постоянной величины равна нулю:

.

2. Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат:

.

3. Если и – независимые случайные величины, то

.

Пример. Вычислить дисперсию дискретной случайной величины , используя данные предыдущего примера.

Решение:

Дисперсию удобно вычислять по формуле D(X) = M(X ²) – M ²(X), где

_.

Таким образом, дисперсия дискретной случайной величины равна

.

Дисперсия имеет размерность квадрата размерности случайной величины. Поэтому для оценки рассеяния возможных значений случайной величины вокруг ее математического ожидания ее использовать неудобно. В связи с этим вводят понятие среднего квадратического отклонения, размерность которого совпадает с размерностью случайной величины.

Определение. Корень квадратный из дисперсии называется средним квадратическим отклонением:

.

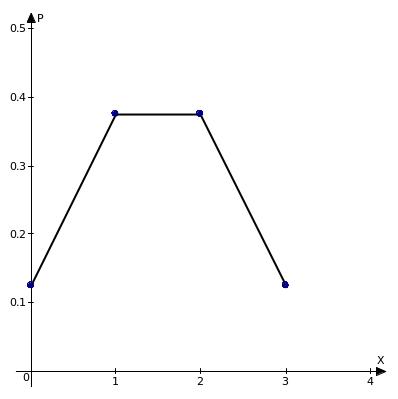
Найти числовые характеристики и построить многоугольник распределения.

Решение.

	0	1	2	3
	0,125	0,375	0,375	0,125

– вероятность рождения девочки

– вероятность рождения мальчика

Найдем числовые характеристики:

1. математическое ожидание

2. дисперсия

3. среднеквадратическое отклонение

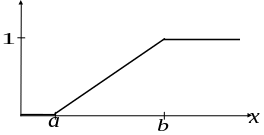
Определение: Функцией распределения НСВ назовем функцию

Функция называется интегральной.

Определение: Плотностью распределения НСВ назовем функцию

Функция называется дифференциальной.

Можно выделить основные законы распределения НСВ:

1. нормальное распределение;

2. распределение ;

3. распределение Стьюдента.

Непрерывные случайные величины обладают следующими характеристиками:

1. математическое ожидание:

2. дисперсия:

3. среднеквадратическое отклонение: