1.1. Элементы комбинаторики.
Комбинаторика – это наука о расположении элементов в определенном порядке и о подсчете числа способов такого расположения.
Существуют два основных правила комбинаторики:
1. Правило « суммы»:
Если элемент
можно выбрать
способами, а элемент
–
способами, то элемент «либо
,
либо
» можно выбрать
способами.
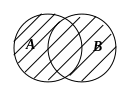
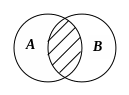
2. Правило « произведения»:
Если элемент
можно выбрать
способами, а элемент
–
способами, то элемент « и
и
» можно выбрать
способами.
Существует 3 типа комбинаций:
1. Перестановки – это такой тип комбинаций, который связан с нумерацией или перестановкой элементов.
Теорема 1. Число перестановок без повторений вычисляется по формуле
Теорема 2. Число перестановок с повторениями вычисляется по формуле
,
где – число повторов.
Пример. Сколько слов можно получить, переставляя буквы в слове « математика»?
2. Сочетания – это такой тип комбинаций, который связан с выбором элементов.
Теорема 3. Число сочетаний без повторений вычисляется по формуле
Пример. Сколько существует способов выбора 3 студентов на конференцию из 20?
Теорема 4. Число сочетаний с повторениями вычисляется по формуле
Пример. В буфете имеются 4 типа пирожных. Сколькими способами можно купить 7 пирожных?
3. Размещения – это такой тип комбинаций, который связан и с выбором и перестановкой элементов.
Теорема 5. Число размещений без повторений вычисляется по формуле
Пример . Сколькими способами можно выбрать старосту и профорга, если в группе 8 человек?
Теорема 6. Число размещений с повторениями вычисляется по формуле
Пример. Сколько существует пятизначных номеров телефонов?
1.2. Классическое определение вероятности
Под вероятностью
(будем обозначать
)
случайного события понимают меру
возможности осуществления данного
события в конкретных условиях эксперимента
(испытания).
При классическом
определении за вероятность события А
принимается отношение числа
благоприятствующих этому событию
элементарных исходов
к общему числу возможных исходов
:
.
Существует ряд задач, в которых и не даны в явном виде, их необходимо находить, используя формулы комбинаторики.
Пример. В кабинете работают 6 мужчин и 4 женщины. Для переезда наудачу отобраны 7 человек. Найти вероятность того, что среди отобранных лиц три женщины.
Решение. Общее число возможных исходов равно числу способов, которыми можно отобрать 7 человек из 10, т.е.
.
Найдем число исходов,
благоприятствующих интересующему нас
событию: трех
женщин можно выбрать из четырех
способами;
при этом остальные четыре человека
должны быть мужчинами, их можно отобрать
способами. Следовательно, число
благоприятствующих исходов равно
.
Искомая вероятность
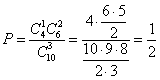
Основные свойства вероятности случайного события.
1. Вероятность достоверного события равна 1.
Действительно, если
событие достоверно, то каждый элементарный
исход испытания благоприятствует
событию. В этом случае
,
следовательно,
.
2. Вероятность невозможного события равна 0.
В этом случае
,
следовательно,
.
3. Вероятность суммы прямого и противоположного событий равна единице.
Пример.
Вероятность выигрыша
лотерейного билета равна 0,001. Найти
вероятность проигрыша.
4. Вероятность произвольного случайного события принимает значения из отрезка [0, 1].
Действительно,
случайному событию благоприятствует
лишь часть из общего числа элементарных
исходов испытания. В этом случае
,
значит
,
следовательно,
.
Итак, вероятность любого события удовлетворяет двойному неравенству
.
Существует ряд задач, в которых и не даны в явном виде, их необходимо находить, используя формулы комбинаторики.