Левому разностному уравнению общего вида

(4.24)

с левыми начальными условиями

(4.25)

соответствует левое рекуррентное уравнение

(4.26)

с левыми начальными условиями

. (4.27)

Например, для левых уравнений 4-го порядка

,

левыми начальными условиями будут следующие

.

Согласно (4.9), (4.11), (4.14) при k=0

Значения находим из рекуррентного уравнения при k=0, а остальные получаем из последней системы

Значения определяется из разностного уравнения при k=0.

Полученные результаты по аналогии распространяются на уравнения более высоких порядков.

Из (4.26) легко получить явную рекуррентную формулу, не прибегая к классической методике решения разностных уравнений.

Пример: Задано левое разностное уравнение, неоднородное второго порядка , причем . Преобразуем это уравнение в рекуррентное .

Так как , то и согласно (8.16) . С учетом этого и разностного и рекуррентного уравнений находим .

Из рекуррентного уравнения находим рекуррентную формулу

и при 0; 1; 2; 3; … получаем значения , ; , ….

Таким образом, алгоритмизация ДУ сводится к преобразованию его сначала в разностное уравнение, а затем в рекуррентное уравнение и рекуррентную формулу, которую можно легко превратить в алгоритмическую модель, реализуемую в виде программы на ЦВМ.

4.2.2 Алгоритмизация ндм на основе z - преобразований

Понятие о z – преобразовании Лапласа. Процесс получения явных рекуррентных соотношений существенно облегчается, если для этого используется дискретное преобразование РФ и, в частности его аналог z – преобразование.

Под z – преобразованием РФ понимают непрерывную функцию

(4.28)

комплексной переменной при условии, что определяющий ее бесконечный ряд сходится. Соответствие оригинала и его - изображения символически записывают в виде .

К основным свойствам - изображений РФ относятся следующие:

а) где

б)

в) запаздывание оригинала изображается

, при ;

г)

д) изображение правых разностей

, при нулевых НУ;

е) изображение левых разностей

, при нулевых НУ;

ж) изображение сумм

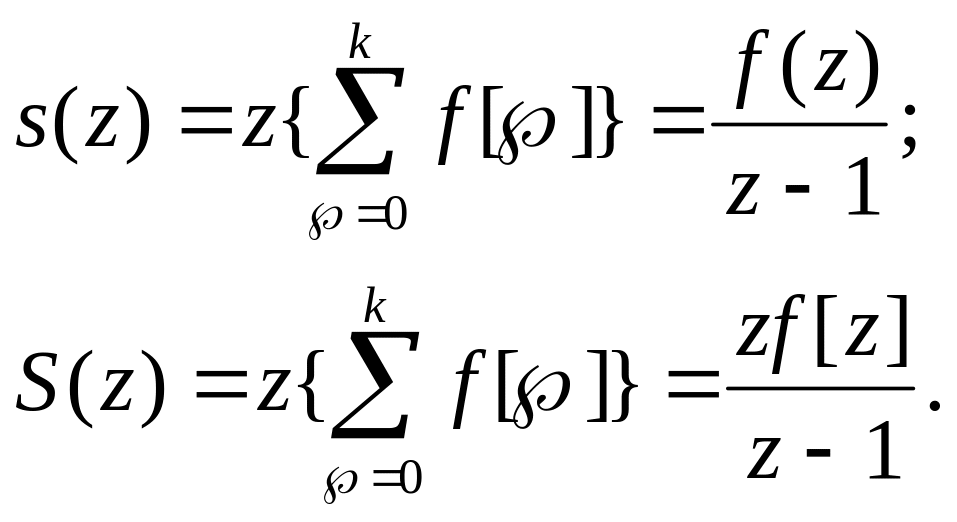
Конечное и начальное значения оригинала

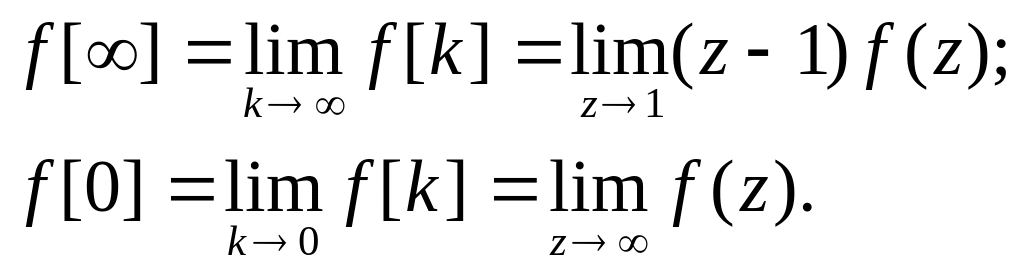
Примерами соответствий являются следующие:

и др.

Они сведены в таблицу соответствий, которую обычно включают в учебники и учебные пособия по теории автоматического управления.

Обратное - преобразование, т.е. определение оригинала по его изображению, выполняется четырьмя способами. Два первых из них аналогичны обратному преобразованию Лапласа для непрерывных функций, два последних аналогов не имеют.

Способы нахождения оригинала по его z-изображению.

Первый способ заключается в непосредственном применении таблицы соответствий оригиналов и - изображений. Если в таблице имеется выражение аналогичное , то соответствующая РФ определяется немедленно.

Пример 1 . Дано Определить . По таблице находим , откуда

Второй способ. Применение таблицы соответствий после разложения на простейшие (табличные) составляющие

. (4.29)

После определения находят

. (4.30)

Обычно -изображения РФ имеют вид

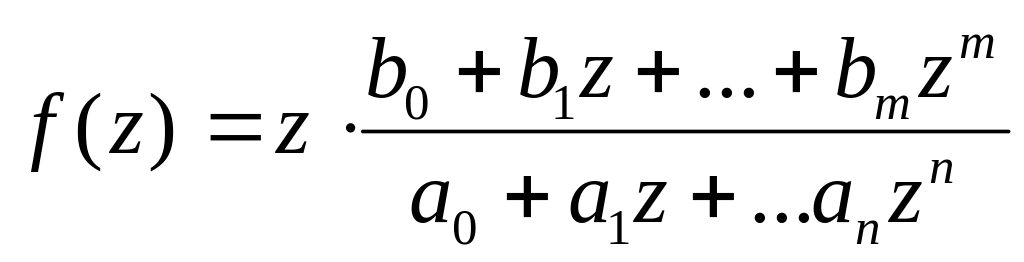, где . (4.31)

Поэтому практически раскладывают на составляющие функцию

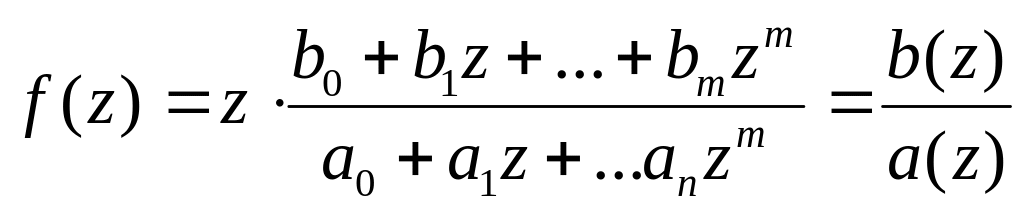. (4.32)

Эта операция реализуется после решения алгебраического уравнения -й степени и определения его корней После чего выполняется разложение

(4.33)

Каждой составляющей соответствует составляющая , которая должна быть приведена к табличному виду.

Пример 2. Дано

Так как то значения коэффициентов определяют из системы уравнений и равны

Таким образом Следовательно Откуда При …

Третий способ. Разложение - изображения по степеням . По определению

(4.34)

Поэтому при разложении (4.31) в ряд (4.34) коэффициенты при равны , т.е являются значениями РФ оригинала при Выражение (4.31) представляют виде так чтобы степени полиномов и были равны . Тогда делением на получают ряд (4.34) для

. (4.35)

Переход от к осуществляют на основании соотношений

; . (4.36)

Пример 3. Дано как в примере 2

.

Делением на получают . Согласно (4.36) . Откуда ….

Четвертый способ. Выражение (4.31) представляют виде

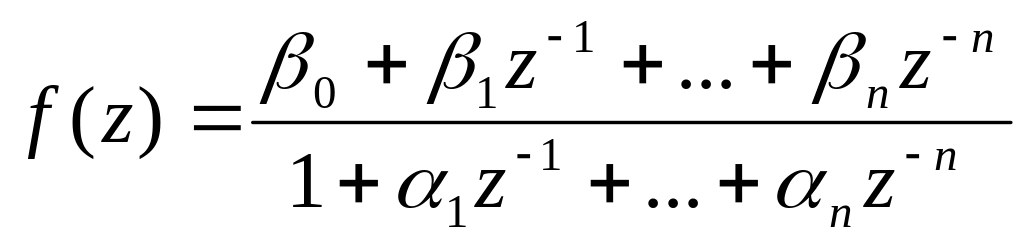. (4.37)

Если принять для простоты , то

.

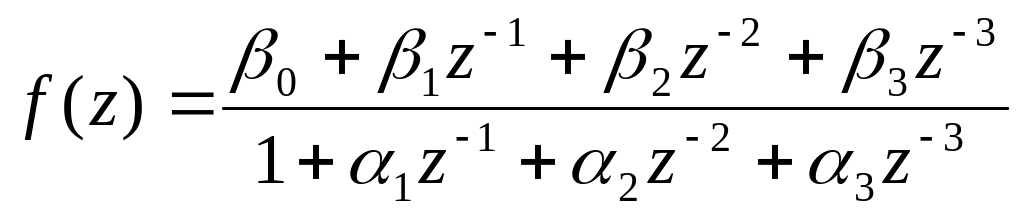Отсюда с учетом (8.34) имеем

.

Откуда, раскрыв скобки и приравняв коэффициенты при одинаковых степенях в правой и левой частях, находят рекуррентные соотношения для и т.д. Эти соотношения легко распространить на общий случай (4.37).

Эффективным способом получения рекуррентных соотношений является использование дискретной передаточной функции (ДПФ).

При нулевых НУ операторная форма разностных и рекуррентных уравнений имеет вид

(4.38)

где , - полиномы . В этом случае возможно представление этих уравнений в форме ДПФ

. (4.39)

Если , то соответствует правым уравнениям, а если , - левым. Располагая ДПФ, можно легко получить -изображение неизвестной РФ

(4.40)

по - изображению известной и затем соответствующее рекуррентное уравнение.

Пример 4. Дана ДПФ , при чем .

Требуется найти рекуррентное уравнение.

Для решения преобразуем ДПФ в операторное уравнение:

После деления на оно имеет вид:

Откуда левое рекуррентное уравнение будет иметь вид:

Таким образом, для алгоритмизации математического описания объекта, полученного в форме передаточной функции, необходимо по ней определить дискретную передаточную функцию, преобразовать ее в операторное уравнение, разделив последнее на , где - старшая степень полинома знаменателя ДПФ, и, используя свойства -преобразования, найти оригинал операторного уравнения, т.е. рекуррентное уравнение.