
- •Практическое занятие №1
- •Практическое занятие №2
- •Получить допуск к работе
- •Наименование, цель занятия, задание;
- •Практическое занятие №3
- •Практическое занятие №3
- •Практическое занятие №4
- •Практическое занятие №4
- •Практическое занятие №6
- •Практическое занятие №5
- •Практическое занятие №7
- •Практическое занятие №8
- •Практическое занятие №8
- •Практическое занятие №9
- •Практическое занятие №10
- •Практическое занятие №11
- •Практическое занятие №12
- •Практическое занятие №12
- •Практическое занятие №13
- •Практическое занятие №13
- •Практическое занятие №14
- •Практическое занятие №14
- •Практическое занятие №15
- •Практическое занятие №16
Практическое занятие №12
Наименование занятия: Координаты вектора в пространстве. Простейшие задачи в координатах
Цель занятия: Научиться находить координаты вектора, решать простейшие задачи в координатах
Подготовка к занятию: Повторить теоретический материал по теме «Координаты вектора в пространстве»
Литература:
Атанасян Л.С. и др. «Геометрия 10-11»
Дадаян А.А. «Математика»
Задание на занятие:
Даны векторы {-1; 2; 0}, {0; -5; 2}, {2; 1; -3}. Запишите разложения этих векторов по координатным векторам , и .
Даны векторы {3; -5; 2}, {0; 7; -1}, . Найти координаты векторов , , , , .
Найти координаты вектора , если а) А(-2; 6; -2), В(3; -1; 0)
б) А , В
Найти длины векторов , = -2 , = +2 -2 .
Даны векторы {3; -2; 1}, {-2; 3; 1}, {-3; 2; 1}. Найти , ,
Найти длину вектора , если А(-1; 0; 2), В(1; -2; 3)
Порядок проведения занятия:
Получить допуск к работе;
Выполнить задания;
Ответить на контрольные вопросы.
Содержание отчета:
Наименование, цель занятия, задание;
Выполненное задание;
Ответы на контрольные вопросы.
Контрольные вопросы для зачета:
Что называется координатными векторами? Как разложить произвольный вектор по координатным векторам?
Как найти длину вектора, если известны его координаты? Координаты точек начала и конца вектора?
Практическое занятие №13
Наименование занятия: Угол между векторами. Скалярное произведение векторов
Цель занятия: Научиться находить угол между векторами, вычислять скалярное произведение векторов
Подготовка к занятию: Повторить теоретический материал по теме «Угол между векторами. Скалярное произведение векторов»
Литература:
Атанасян Л.С. и др. «Геометрия 10-11»
Дадаян А.А. «Математика»
Задание на занятие:
Угол между векторами и
 равен .
Найти углы между векторами
равен .
Найти углы между векторами
 и
и
 ,
и
,
и
.
,
и
,
и
.Даны векторы {1; -1; 2}, {-1; 1; 1}, {5; 6; 2}. Вычислить
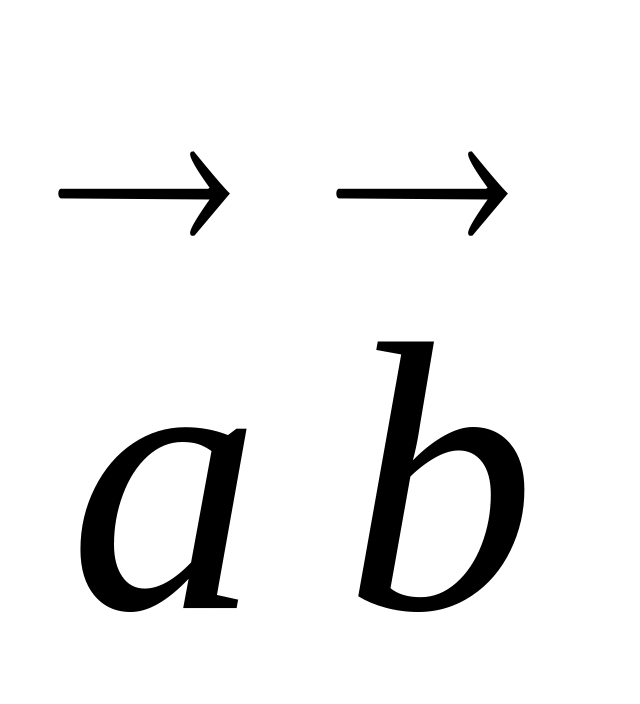 ,
,
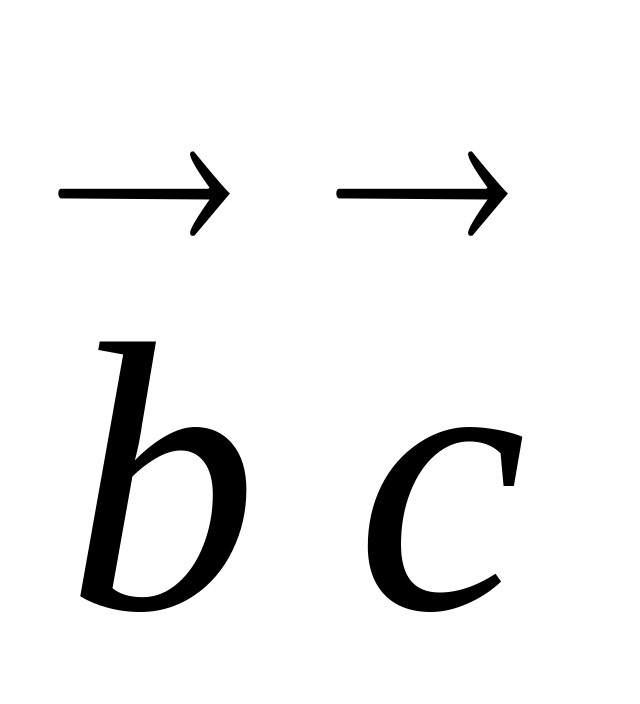 ,
,
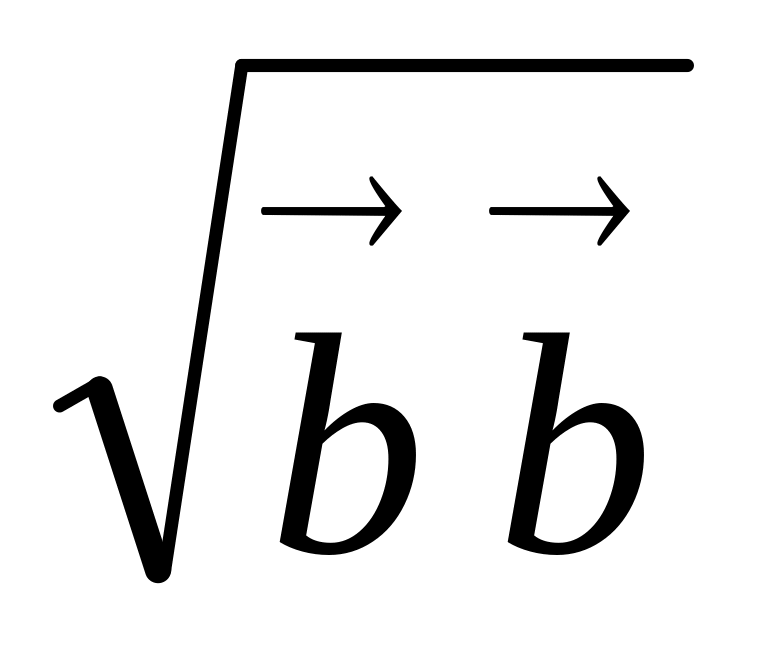 .
.Даны векторы = т +3 +4 и = 4 +т -7 . При каком значении т векторы и перпендикулярны?
Вычислить угол между векторами {2; -2; 0} и {3; 0; -3}; {0; 5; 0} и
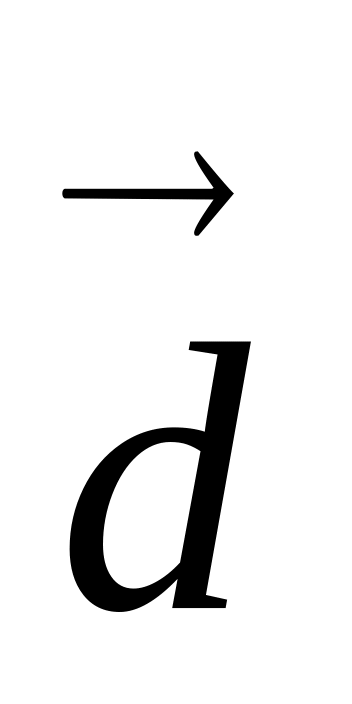 {0;
{0;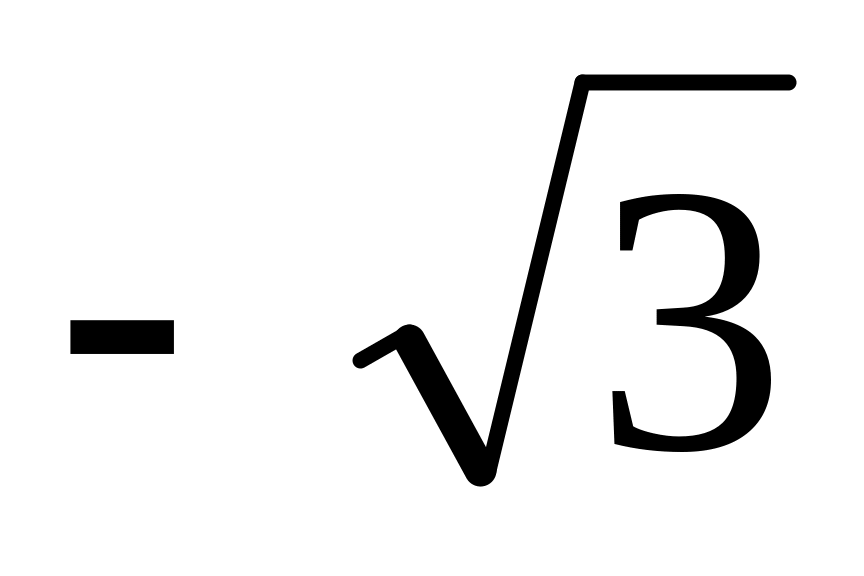 ;
1}.
;
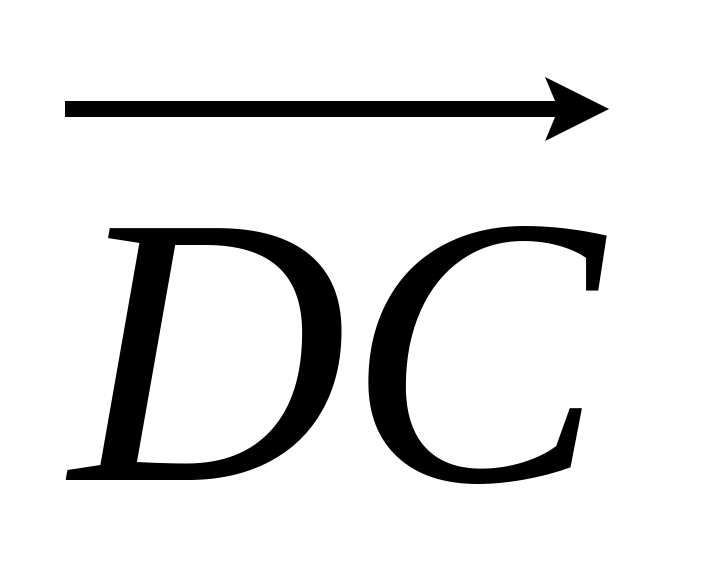
1}.Вычислить угол между прямыми АВ и СD, если А(3; 2; -4), В(4; -1; 2), С(6; -3; 2), D(7; -3; 1).
Порядок проведения занятия:
Получить допуск к работе;
Выполнить задания;
Ответить на контрольные вопросы.
Содержание отчета:
Наименование, цель занятия, задание;
Выполненное задание;
Ответы на контрольные вопросы.
Контрольные вопросы для зачета:
Что называется скалярным произведением векторов?
Как вычислить скалярное произведение по известным координатам вектора?
Как найти угол между векторами?
