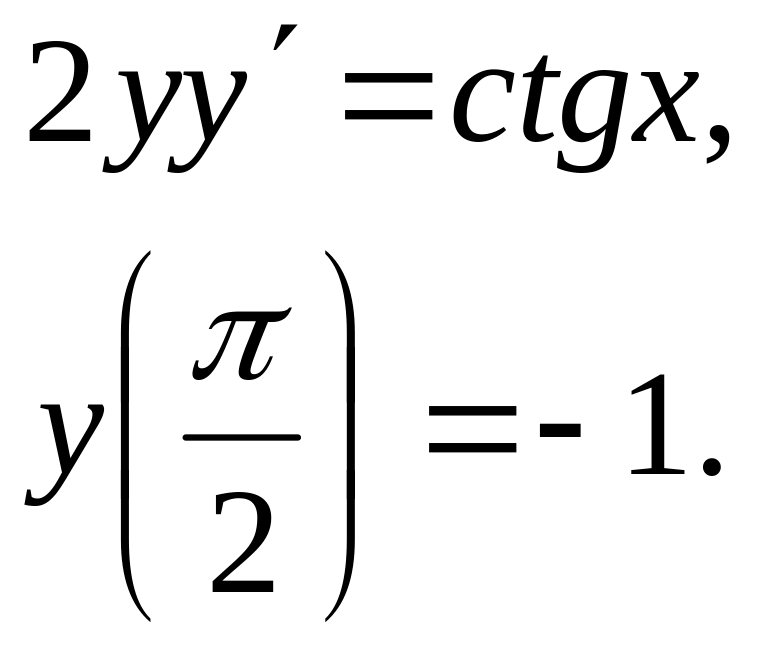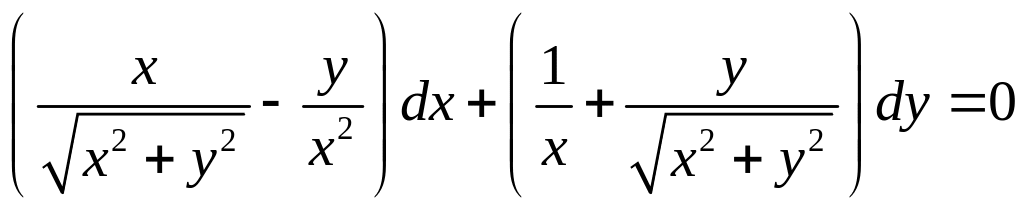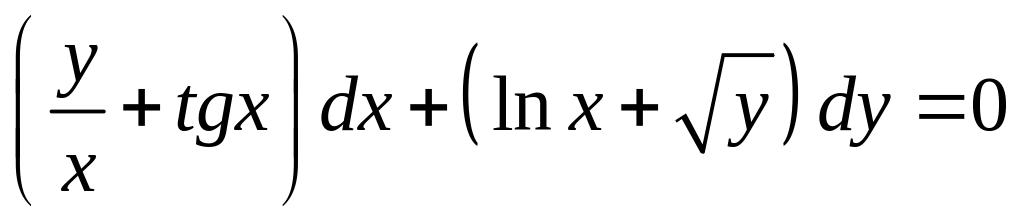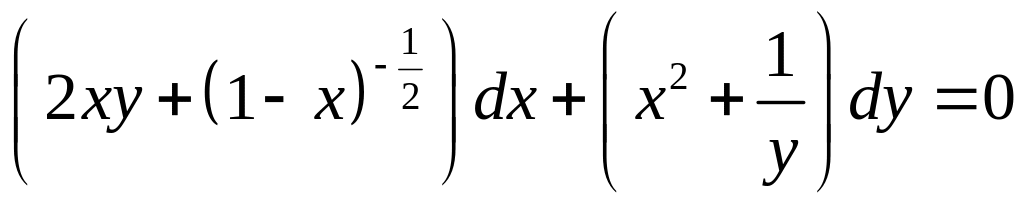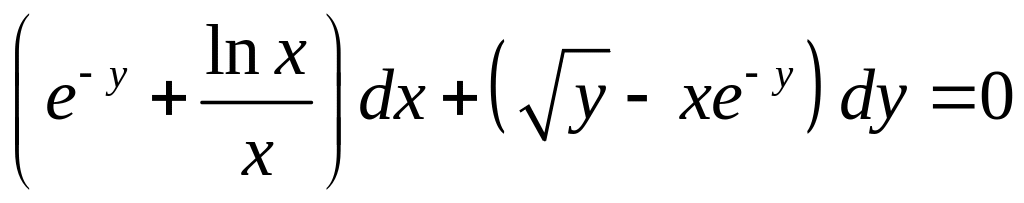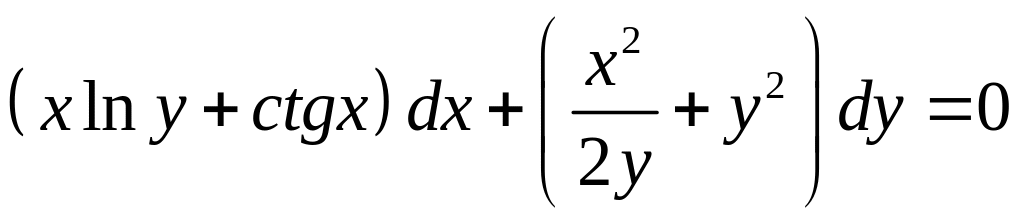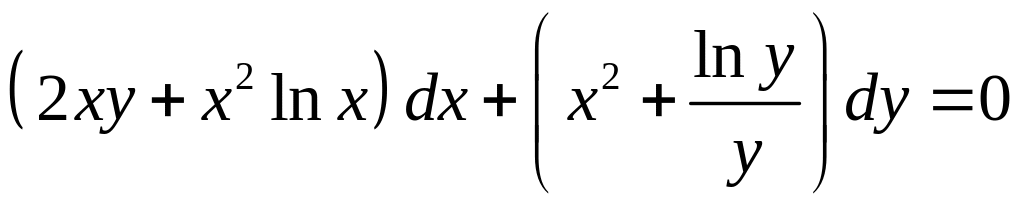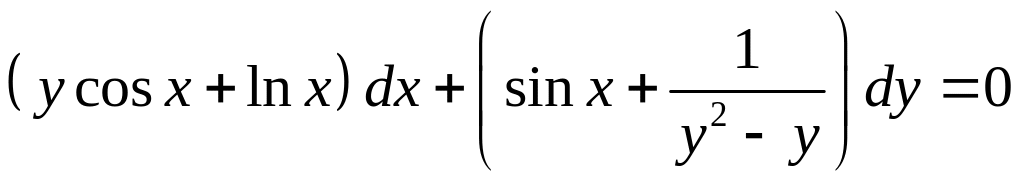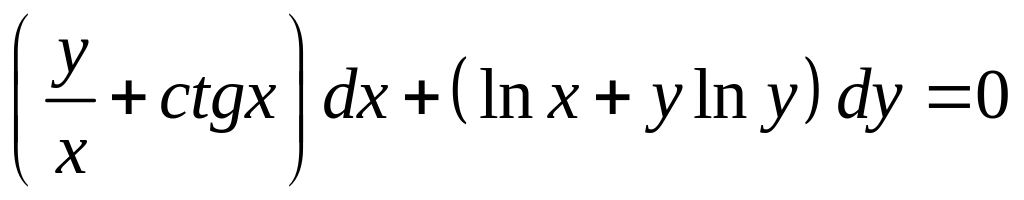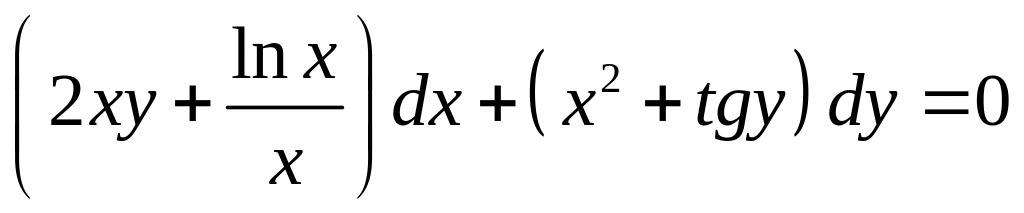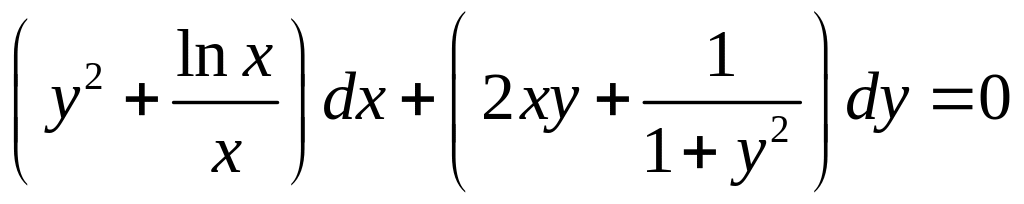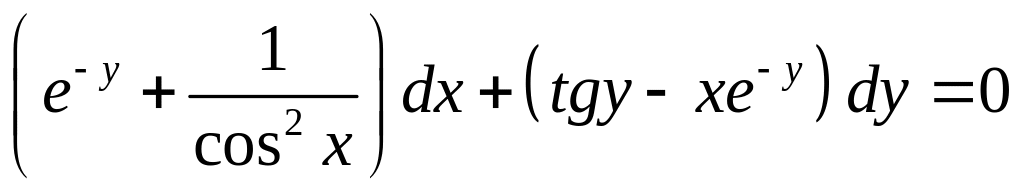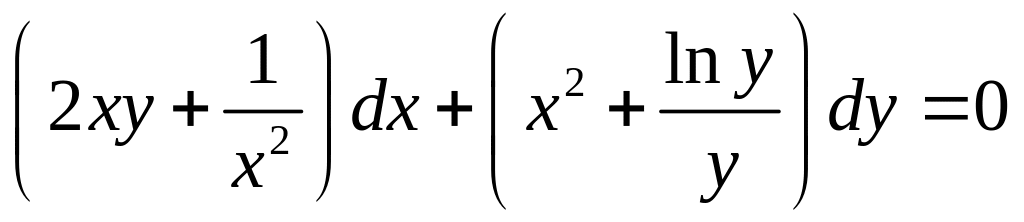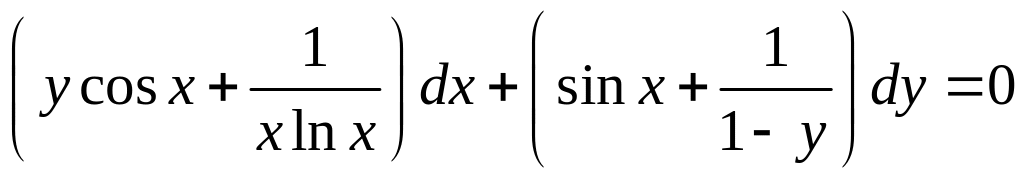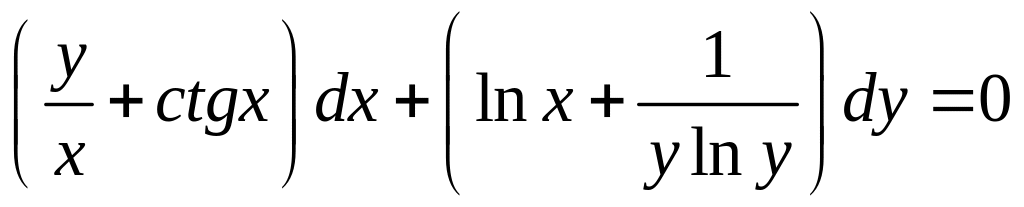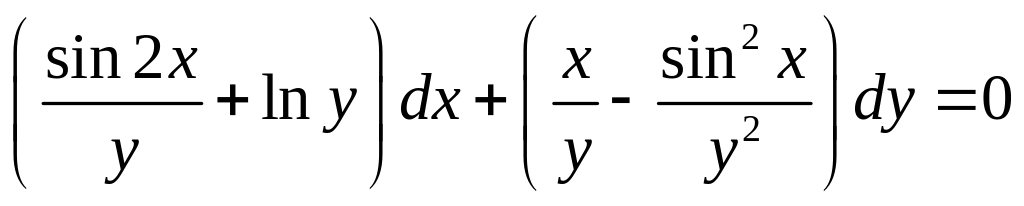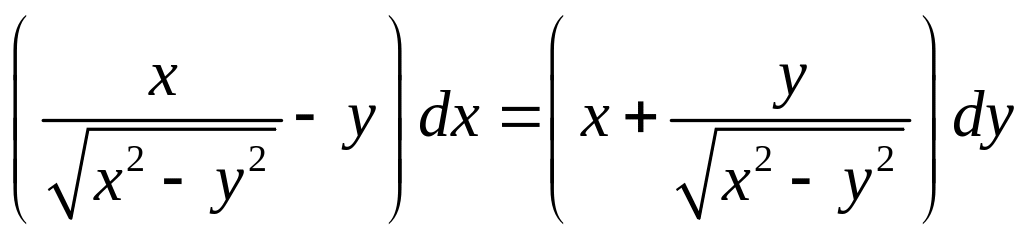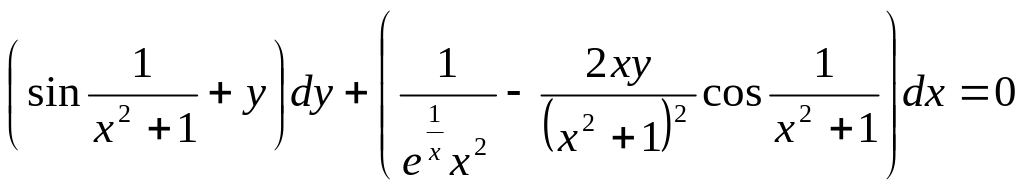Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:Методичка_Тышлек_ДУ.doc
X
- •Уравнения первого порядка
- •Уравнения с разделяющимися переменными
- •Однородные уравнения
- •Линейные уравнения и уравнения Бернулли
- •Уравнения в полных дифференциалах
- •Решить уравнения, найдя интегрирующий множитель либо сделав замену переменных
- •Уравнения, не разрешенные относительно производной a) неполные уравнения
- •Б) уравнения, содержащие и .
- •В) уравнения Лагранжа и Клеро
- •Разные уравнения первого порядка
- •Уравнения, допускающие понижение порядка
- •Найти решение задачи Коши для уравнения высокого порядка
- •Решить уравнения
- •Линейные уравнения
- •Неоднородные уравнения с постоянными коэффициентами (метод неопределенных коэффициентов): а) найти вид частного решения неоднородного уравнения
- •Б) найти общее решение
- •В) найти решение задачи Коши
- •Найти общее решение неоднородного уравнения с постоянными коэффициентами (метод вариации произвольных постоянных)
- •Уравнение Эйлера
- •Функция Грина краевой задачи для линейного уравнения второго порядка
- •Уравнения с переменными коэффициентами
- •Линейные системы
- •Линейные однородные системы (метод Эйлера)
- •Линейные неоднородные системы:
- •Устойчивость по Ляпунову. Нелинейные системы.
- •Исследовать на устойчивость по первому приближению а) исследовать нулевое решение системы
- •Б) исследовать все точки покоя системы
- •В) исследовать, при каких значениях параметров асимптотически устойчиво нулевое решение системы
- •Решить нелинейные системы
- •Уравнения с частными производными первого порядка.
- •Геометрические и физические задачи
- •1.1 Уравнения с разделяющимися переменными
- •1.2 Однородные уравнения
- •1.3 Линейные уравнения
- •1.6 Уравнения, не разрешенные относительно производной
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]