4.2. Частные производные и дифференциал высших порядков
Пусть функция
определена
и непрерывна вместе со своими первыми
частными производными в некоторой точке
.
Частные производные
по переменным
от производных первого порядка называются
частными
производными второго порядка и
обозначаются
, 
.
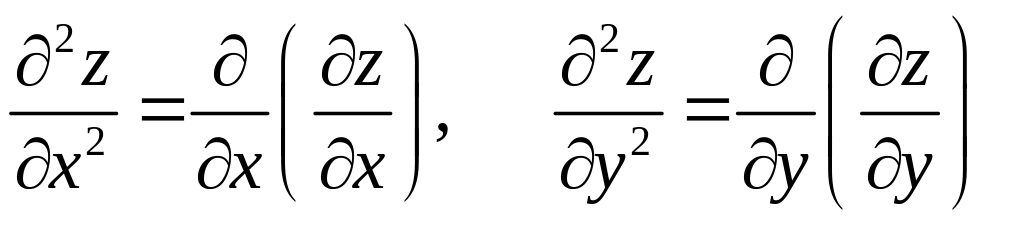Производные
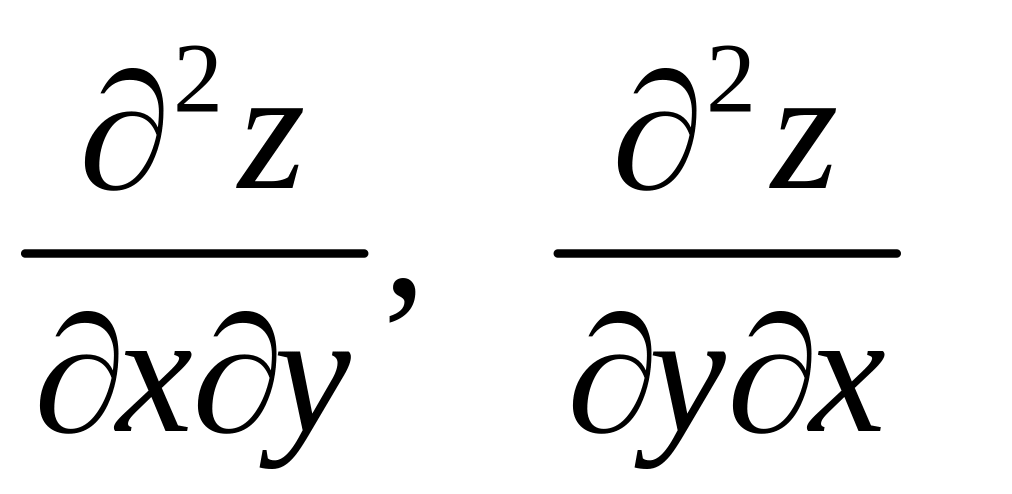называются
смешанными
производными.
Если смешанные
производные
непрерывны,
то справедливо равенство
.
Полным дифференциалом второго порядка функции называется дифференциал от ее полного дифференциала, который обозначается
.
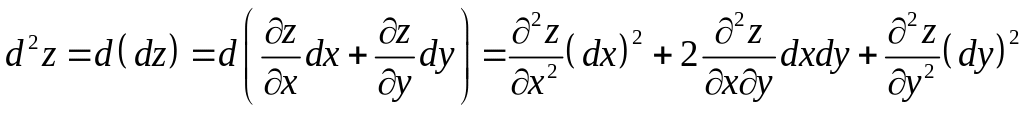4.3. Экстремум функции нескольких переменных
Пусть функция
определена в области
.
Функция
имеет в точке
локальный
максимум (минимум),
равный
,
если существует такая
– окрестность этой точки, что для всех
отличных от
точек
из этой окрестности имеет место
неравенство
.
Необходимые
условия экстремума.
Если функция
в точке
имеет локальный экстремум, то в этой
точке обе частные производные, если они
существуют, равны нулю или хотя бы одна
из них в этой точке не существует.
Если – точка экстремума дифференцируемой функции
,
то 
. (4.4)
Из этой системы уравнений находят стационарные точки.
Сформулируем достаточные условия существования экстремума.
Пусть
,
где
– стационарная точка дважды дифференцируемой
функции
.
Тогда:
1) если
,
то
имеет в точке
локальный экстремум (при
– локальный максимум, при
– минимум);
2) если
,
экстремума в точке
нет;
3) если
,
функция может иметь, а может и не иметь
локальный экстремум.
Пример 4.3.
Найти локальные экстремумы функции
.
Решение. Областью определения данной функции является вся плоскость.
Находим частные производные первого порядка и составляем систему уравнений (4.4):
.
Решая эту систему,
получим две стационарные точки
и
.
Находим частные
производные второго порядка:
.
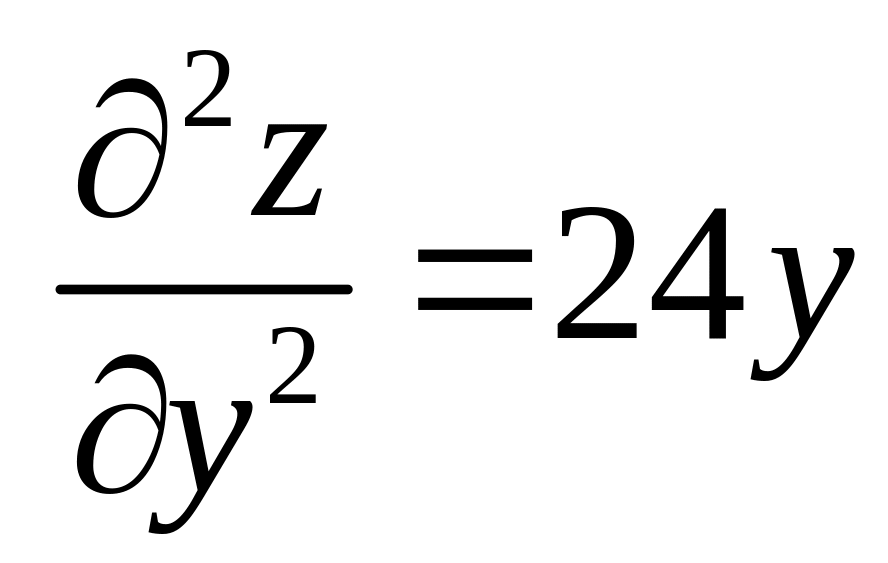Вычисляем их значения в точках
и
.
В точке
:
.
Тогда имеем
.
Следовательно, точка
не является точкой экстремума.
В точке
:
.
Тогда
.
Так как
,
то точка
– точка локального минимума.
Вычисляем
.
Задание
8.
Дана функция
,
точка
и вектор
.
Найти в точке М: а) дифференциал
;
б) производную
по направлению вектора
;
в) градиент
.
8.1.
.
8.2.
.
8.3.
.
8.4.
.
8.5.
.
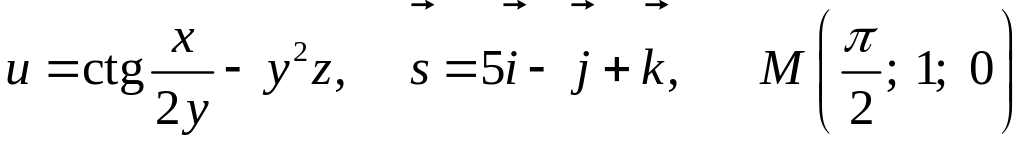8.6.
.
8.7.
.
8.8.
.
8.9.
.
8.10.
.
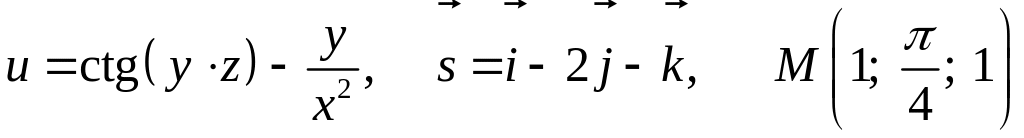8.11.
.
8.12.
.
8.13.
.
8.14.
.
8.15.
.
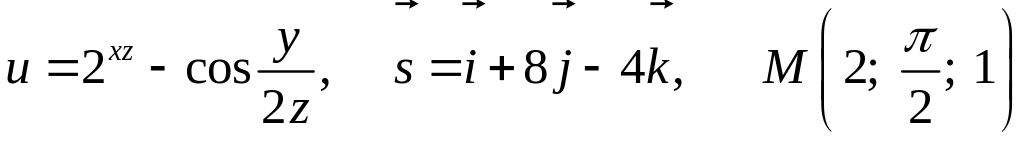8.16.
.
8.17.
.
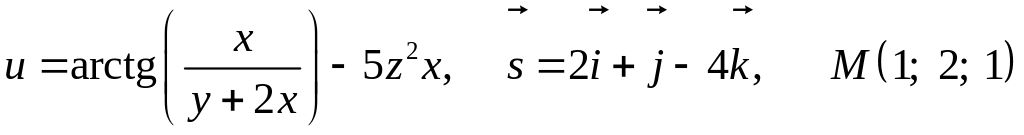8.18.
.
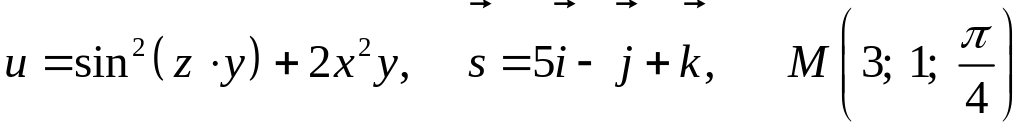8.19.
.
8.20.
.
8.21.
.
8.22.
.
8.23.
.
8.24.
.
8.25.
.
8.26.
.
8.27.
.
8.28.
.
8.29.
.
8.30.
.
Задание 9. Найти локальные экстремумы функции .
9.1.
.
9.2.
.
9.3.
.
9.4.
.
9.5.
.
9.6.
.
9.7.
.
9.8.
.
9.9.
.
9.10.
.
9.11.
9.12.
.
9.13.
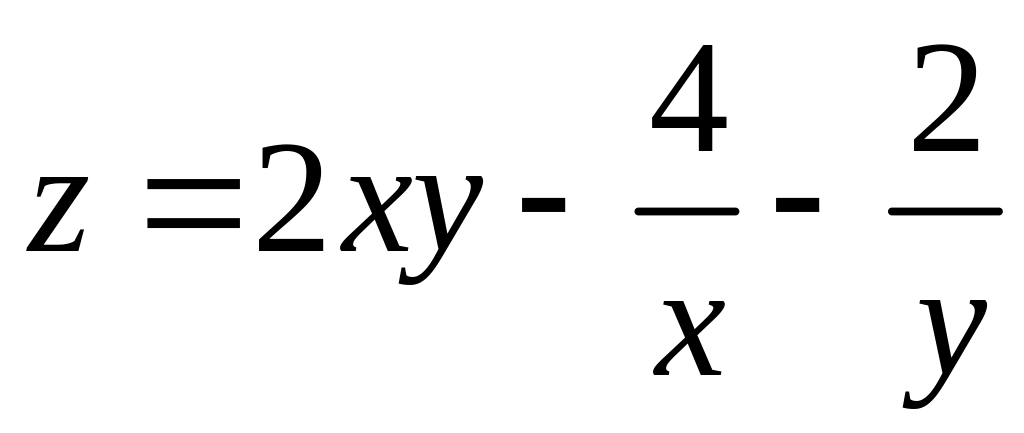. 9.14.
.
9.15.
.
9.16.
.
9.17.
.
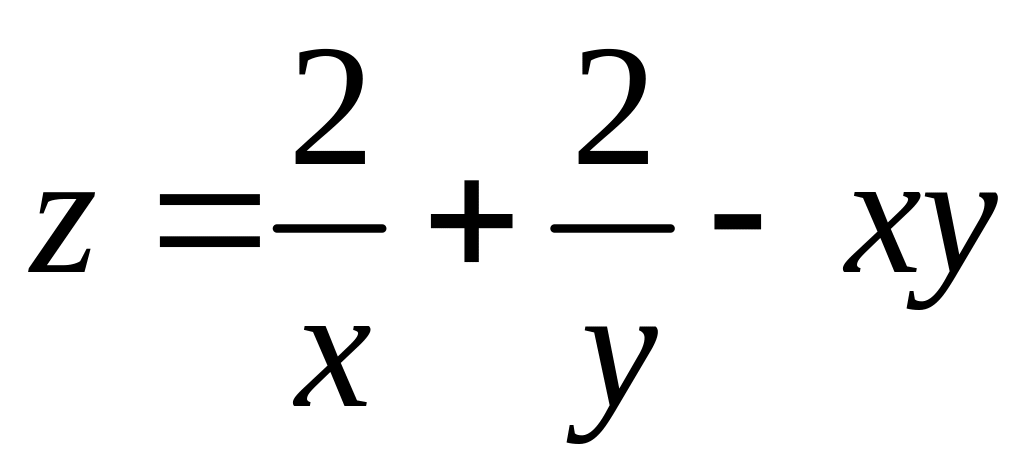9.18.
.
9.19.
.
9.20.
.
9.21.
.
9.22.
.
9.23.
.
9.24.
.
9.25.
.
9.26.
.
9.27.
.
9.28.
.
9.29.
.
9.30.
.