
- •Тема 1. Элементы линейной алгебры
- •1.1. Решение невырожденных систем линейных уравнений
- •1.2. Решение произвольных систем линейных уравнений
- •Тема 2. Векторная алгебра. Аналитическая геометрия
- •2.1. Векторы. Скалярное, векторное и смешанное произведение векторов
- •2.2. Плоскость и прямая в пространстве
- •Тема 3. Введение в математический анализ. Дифференциальное исчисление функции одной переменной
- •3.1. Предел функции. Основные способы вычисления пределов
- •Правило дифференцирования сложной функции
- •Дифференцирование неявных функций
- •Дифференцирование функций, заданных параметрически
- •Дифференцирование степенно-показательной функции
- •3.2. Производные высших порядков
- •3.3. Исследование функций и построение графиков
- •Построение графика функции
- •Тема 4. Дифференциальное исчисление функции нескольких переменных
- •4.1. Понятие функции нескольких переменных и ее предела
- •4.2. Частные производные и дифференциал высших порядков
- •4.3. Экстремум функции нескольких переменных
- •Литература
- •1.1. Решение невырожденных систем линейных уравнений 2
Построение графика функции
Исследование функции и построение ее графика можно проводить по следующей схеме:
Найти область определения функции.
Исследовать функцию на четность (нечетность) и периодичность. Найти точки пересечения графика с осями координат.
Найти точки разрыва функции и асимптоты кривой.
Определить интервалы монотонности и локальные экстремумы функции.
Найти интервалы выпуклости и вогнутости и точки перегиба графика функции.
Построить график функции.
Пример 3.16.
Исследовать функцию
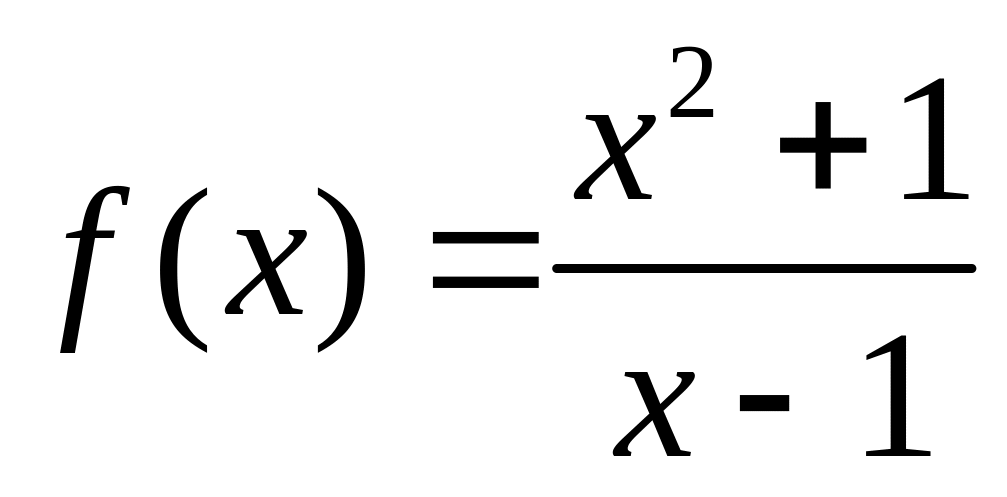 и построить ее график.
и построить ее график.
Решение.
1. Находим область определения
![]() .
.
2. Поскольку
![]() ,
то функция не является четной, нечетной
и периодической.
,
то функция не является четной, нечетной
и периодической.
Находим точки пересечения с осями координат:
а) так как
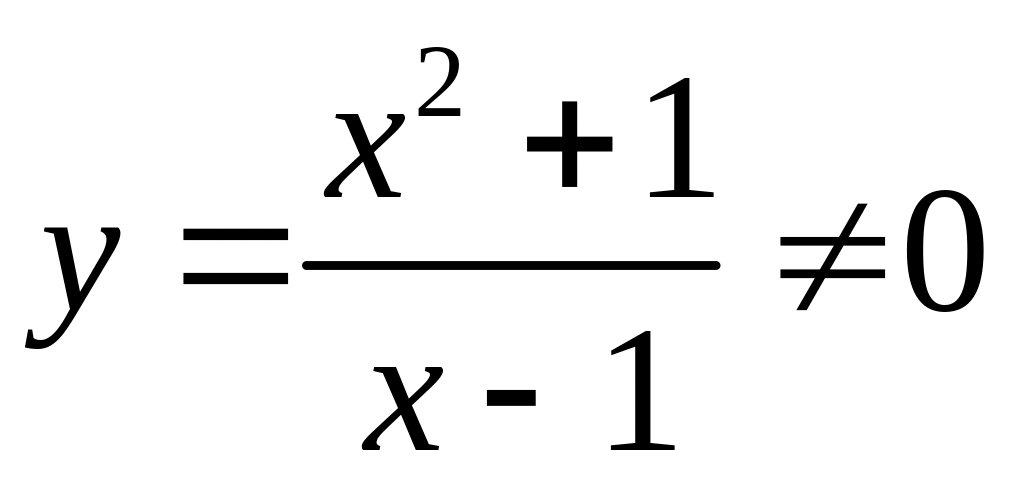 ,
то график функции не пересекает ось
,
то график функции не пересекает ось
![]() ;
;
б) при
![]() график функции пересекает ось Оу
в точке
график функции пересекает ось Оу
в точке
![]() .
.
3. Функция не
определена в точке
![]() .
Поскольку
.
Поскольку
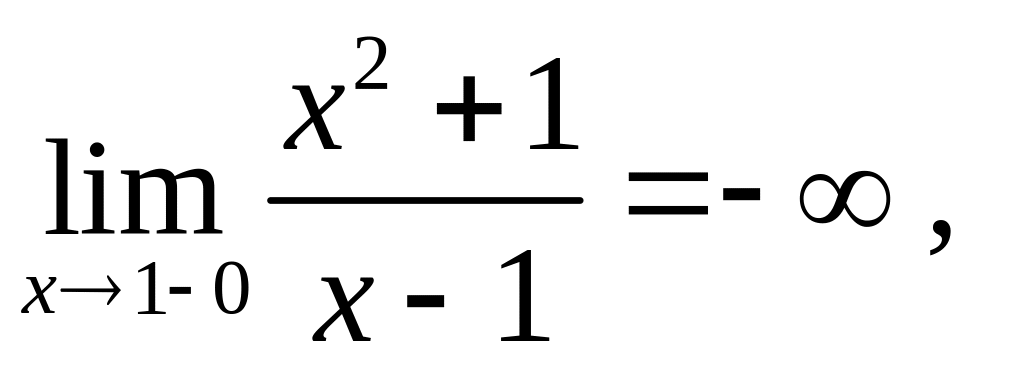
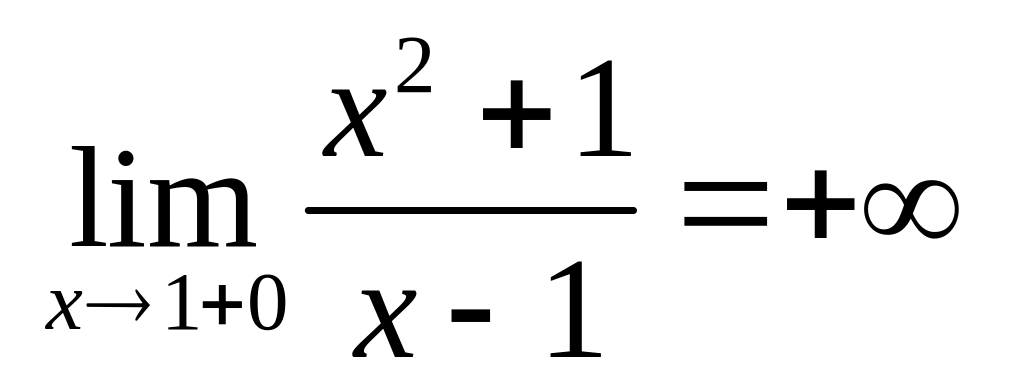 ,
то
– точка разрыва второго рода. Так как
,
то
– точка разрыва второго рода. Так как
![]() ,
то прямая
есть вертикальная асимптота.
,
то прямая
есть вертикальная асимптота.
Далее находим
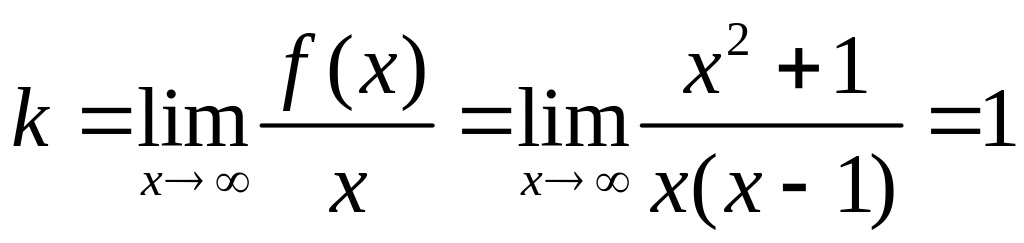 ,
,
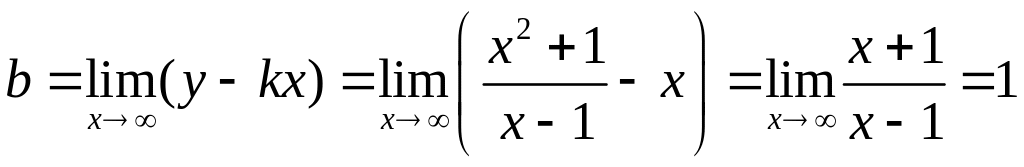 .
.
Следовательно,
прямая
![]() есть наклонная асимптота.
есть наклонная асимптота.
4. Вычислим
 .
.
Первая производная
не существует в точке
,
которая не принадлежит области
определения
![]() и, следовательно, не является критической
точкой.
и, следовательно, не является критической
точкой.
При
![]() получаем
получаем
![]() или
или
![]() .
Точки
и
являются критическими (стационарными)
точками.
.
Точки
и
являются критическими (стационарными)
точками.
Определим интервалы
монотонности из неравенств
![]() и
и
![]() :
:
 при
при
![]() ;
;
 при
при
![]() .
.
Следовательно, функция возрастает при и убывает при .
В точке
![]() функция
имеет максимум
функция
имеет максимум
![]() =
=![]() .
.
В точке
![]() функция
имеет минимум
функция
имеет минимум
![]() =
=![]() .
.
5. Находим
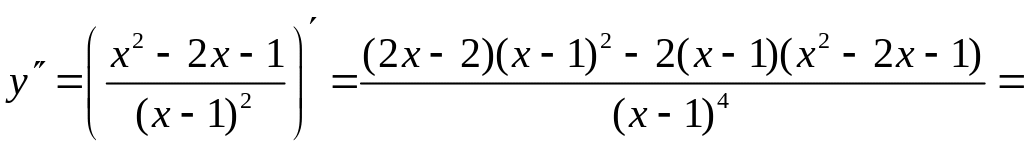
 .
.
Определяем интервалы
выпуклости и вогнутости графика функции
из неравенств
![]() .
Имеем
.
Имеем
![]() при
при
![]() ,
,
![]() при
при
![]() .
Следовательно, кривая выпукла на
.
Следовательно, кривая выпукла на
![]() и вогнута на
и вогнута на
![]() .
Так как
не принадлежит области определения
функции и
.
Так как
не принадлежит области определения
функции и
![]() ,
то точек перегиба нет.
,
то точек перегиба нет.
Результаты исследования функции заносим в таблицу.
|
|
|
|
1 |
|
|
|
|
+ |
0 |
– |
не сущ. |
– |
0 |
+ |
|
– |
– |
– |
не сущ. |
+ |
+ |
+ |
|
|
- 0,83 max |
|
не сущ. |
|
4,83 min |
|
6. Исходя из результатов таблицы строим график данной функции.
 Y
Y
1
0 X
1
![]() -
1
-
1
Задание 4. Вычислить пределы функций, не пользуясь правилом Лопиталя–Бернулли.
4.1. а)
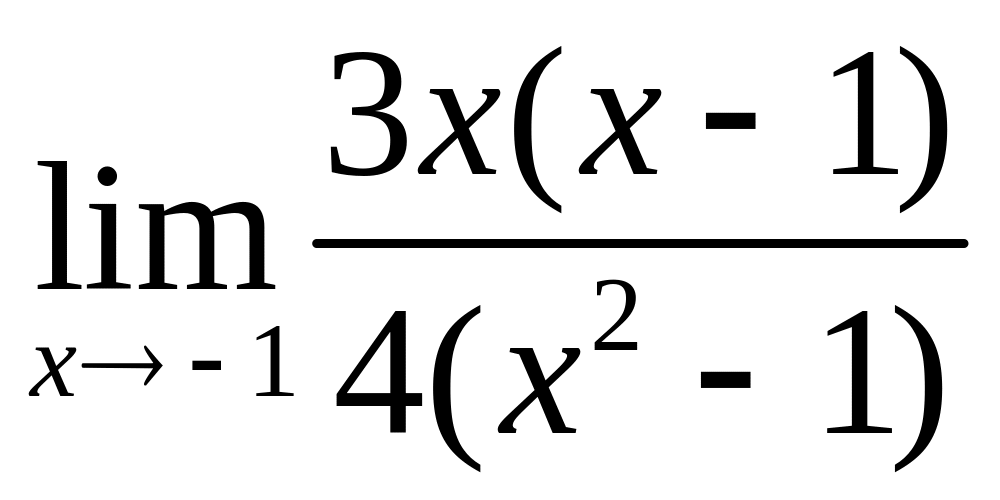 , б)
, б)
![]() , в)
, в)
 .
.
4.2. а)
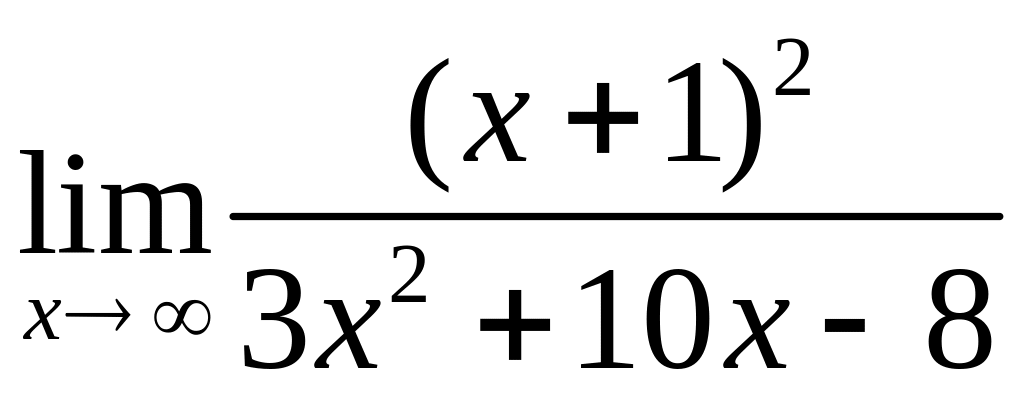 , б)
, б)
![]() , в)
, в)
![]() .
.
4.3. а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
 .
.
4.4. а)
 , б)
, б)
 , в)
, в)
![]() .
.
4.5. а)
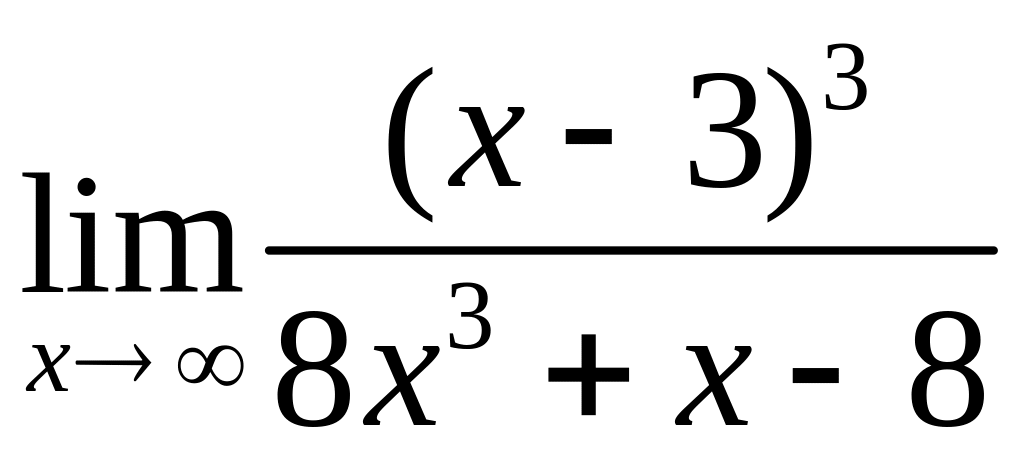 , б)
, б)
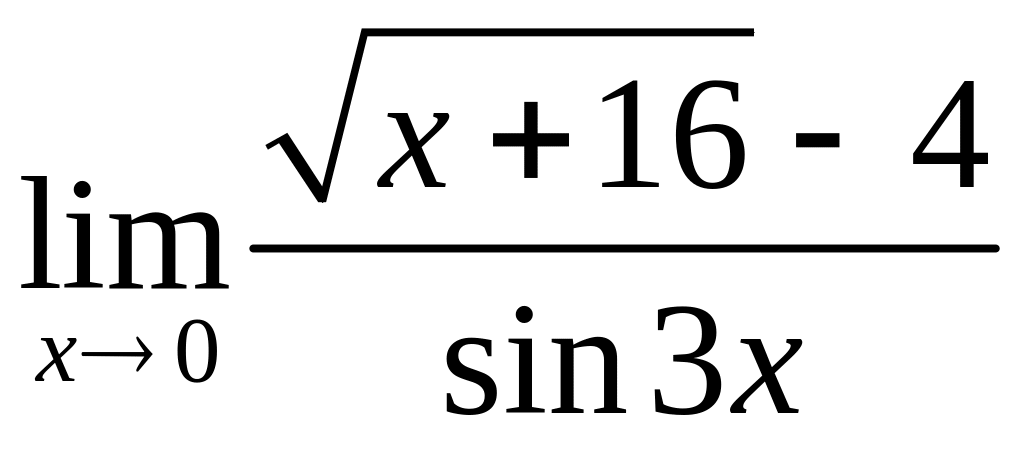 , в)
, в)
 .
.
4.6. а)
 , б)
, б)
![]() , в)
, в)
![]() .
.
4.7. а)
 , б)
, б)
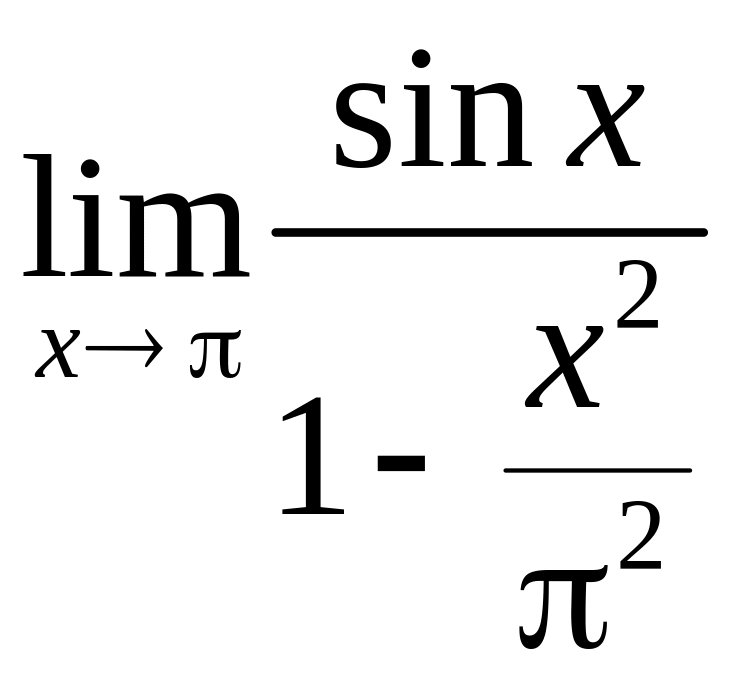 , в)
, в)
![]() .
.
4.8. а)
 , б)
, б)
![]() , в)
, в)
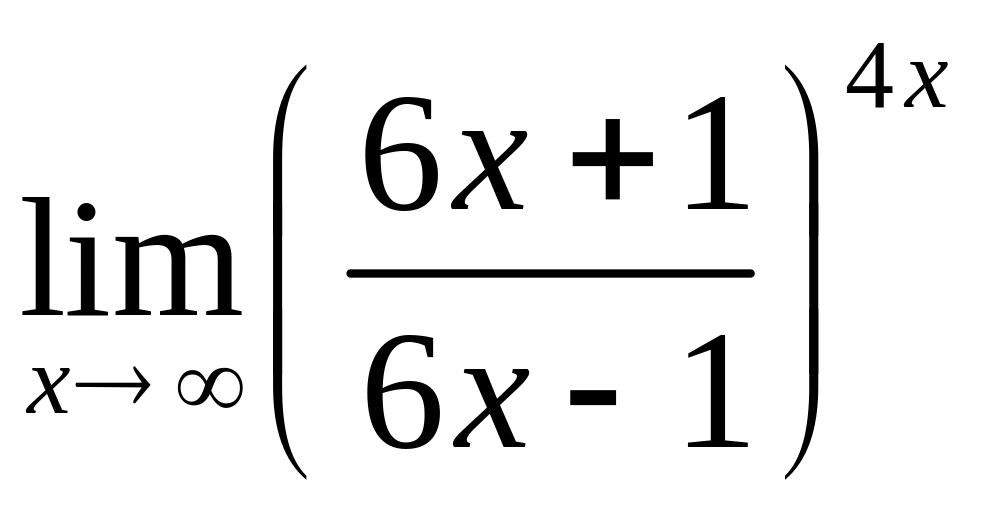 .
.
4.9. а)
 , б)
, б)
 , в)
, в)
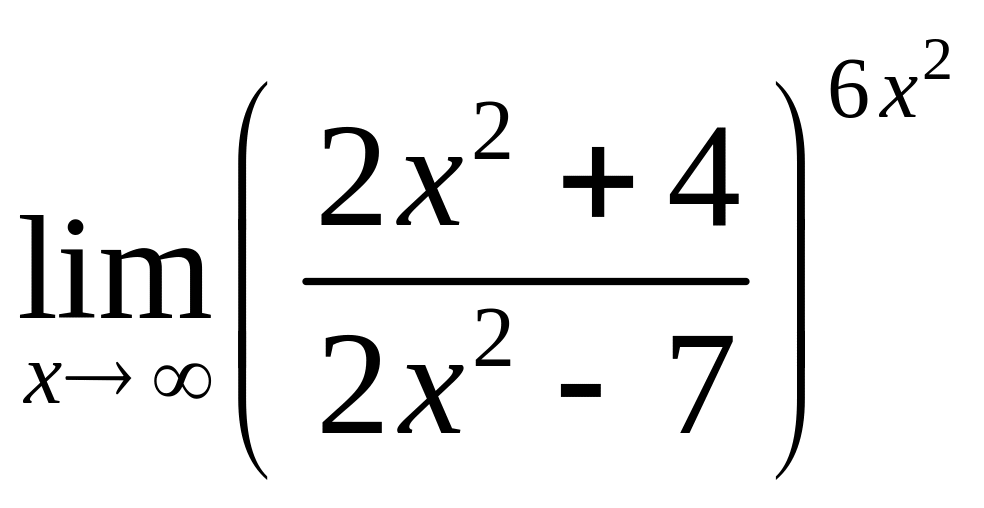 .
.
4.10. а)
 , б)
, б)
![]() , в)
, в)
 .
.
4.11. а)
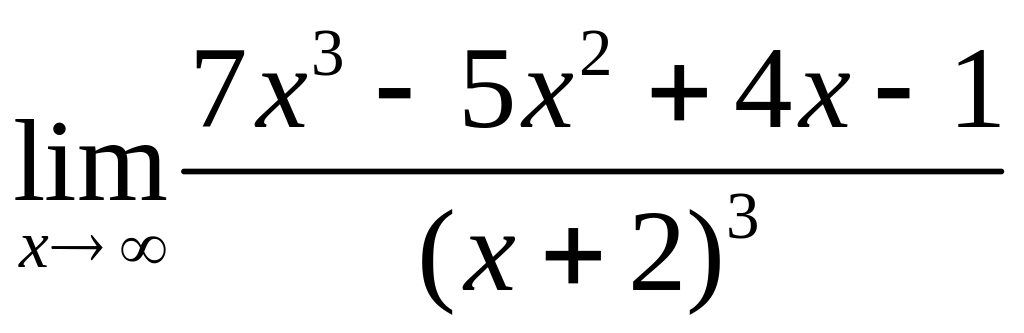 ,
б)
,
б)
 ,
в)
,
в)
![]() .
.
4.12. а)
 , б)
, б)
 , в)
, в)
![]()
4.13. а)
 , б)
, б)
 , в)
, в)
![]()
4.14. а)
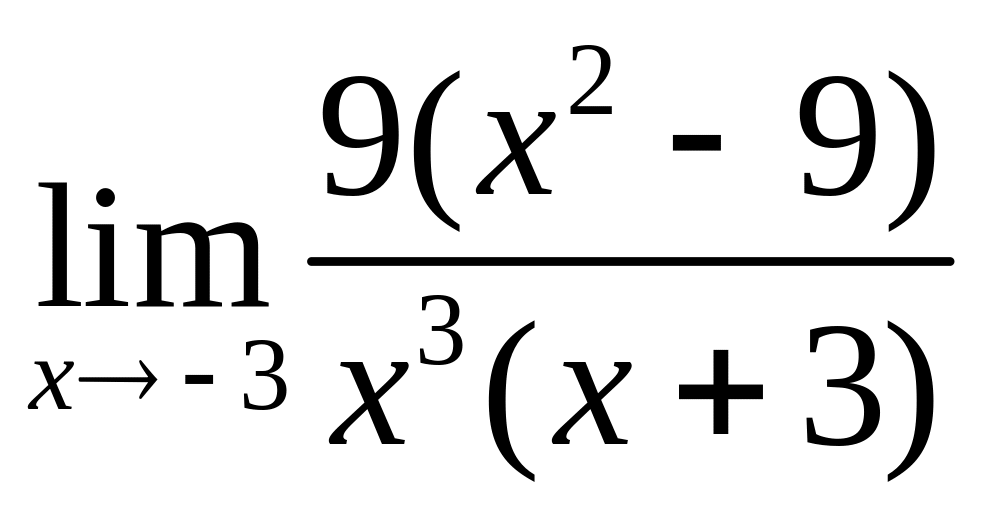 , б)
, б)
![]() ,
в)
,
в)
![]() .
.
4.15. а)
![]() ,
б)
,
б)
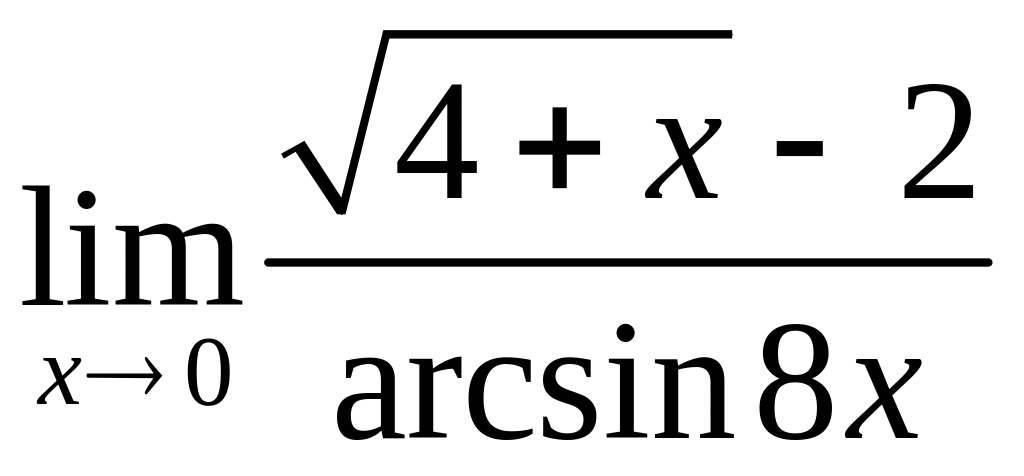 , в)
, в)
![]() .
.
4.16. а)
 , б)
, б)
 , в)
, в)
![]() .
.
4.17. а)
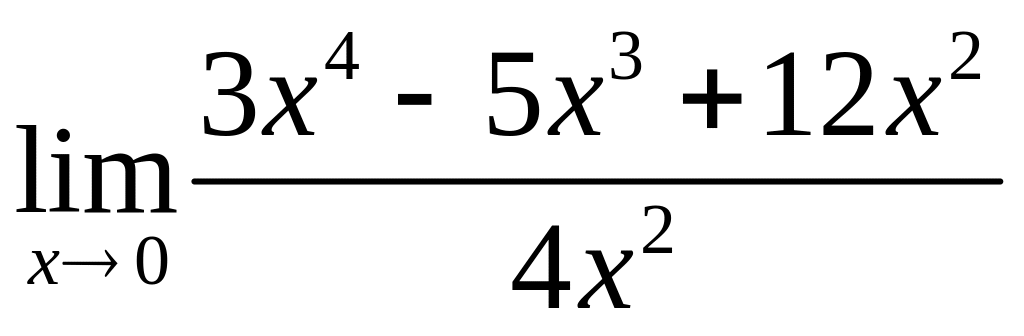 ,
б)
,
б)
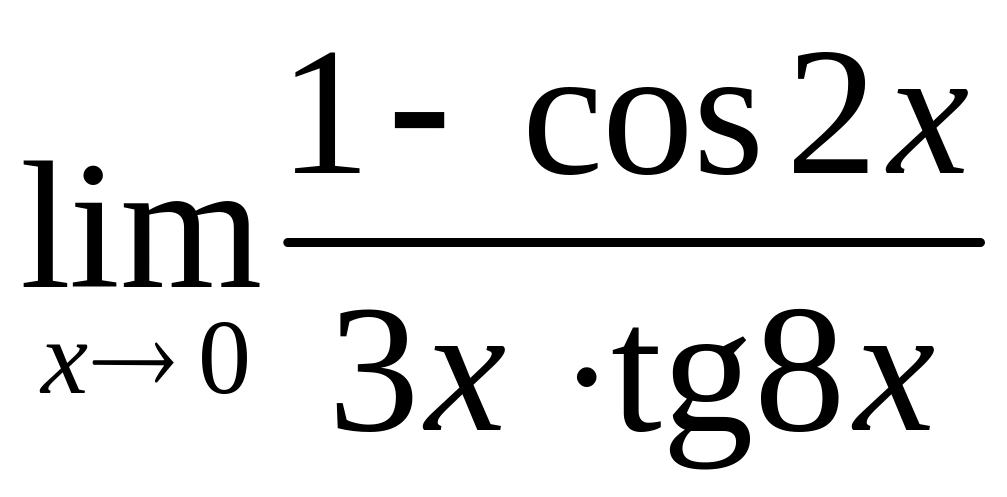 ,
в)
,
в)
![]() .
.
4.18. а)
 ,
б)
,
б)
 ,
в)
,
в)
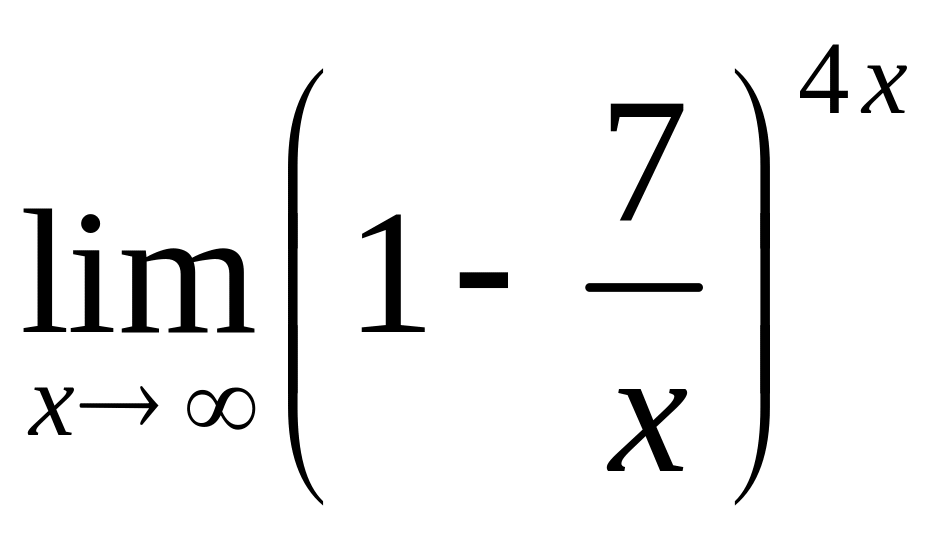 .
.
4.19. а)
 ,
б)
,
б)
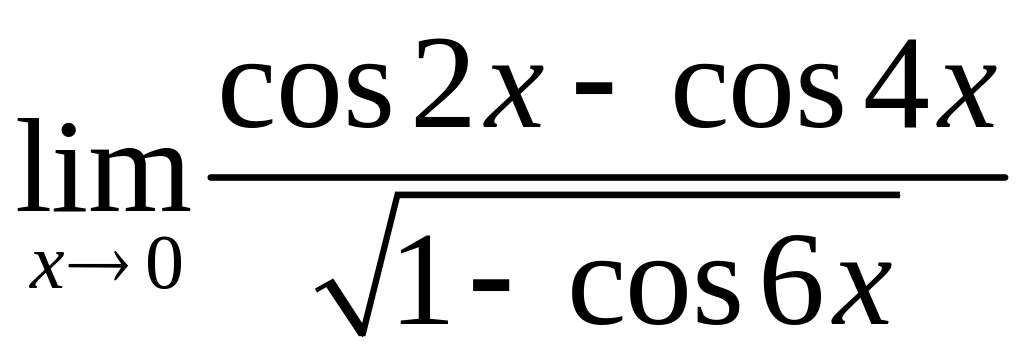 ,
в)
,
в)
![]() .
.
4.20. а)
 ,
б)
,
б)
 ,
в)
,
в)
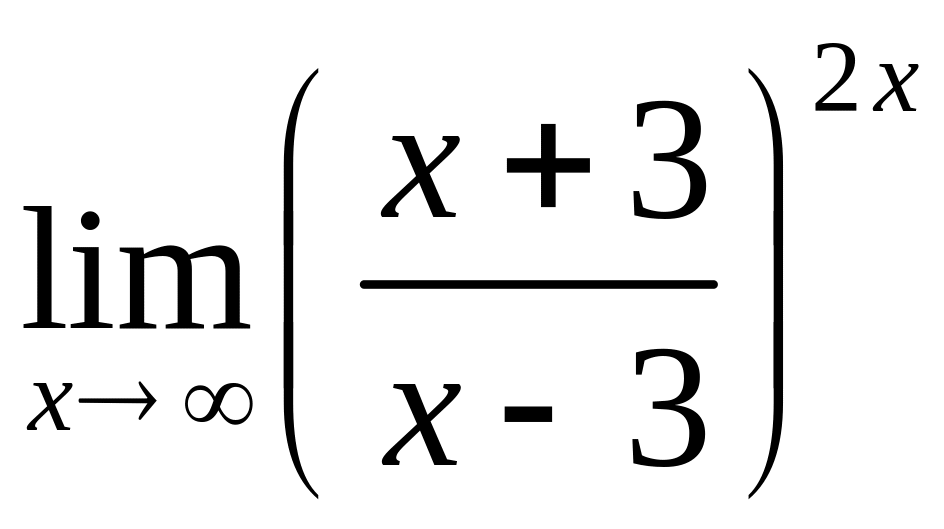 .
.
4.21. а)
 ,
б)
,
б)
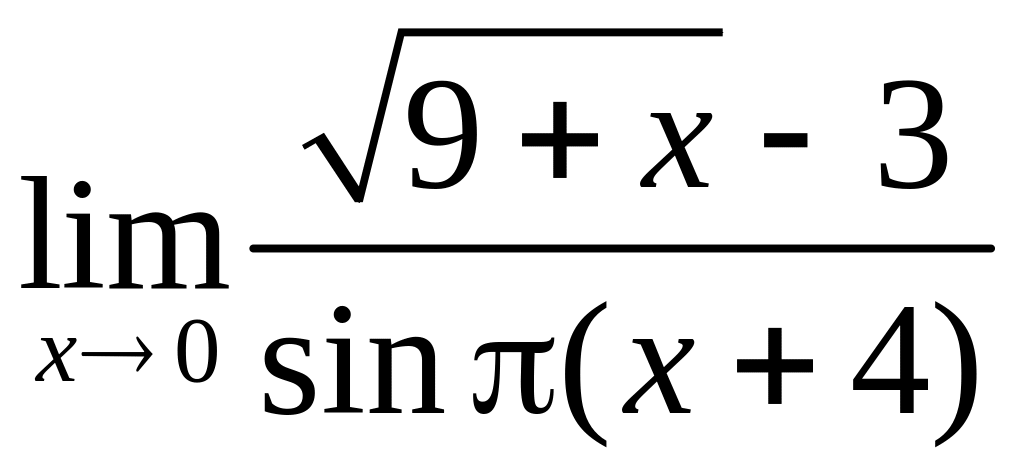 ,
в)
,
в)
![]() .
.
4.22. а)
 ,
б)
,
б)
![]() ,
в)
,
в)
![]() .
.
4.23. а)
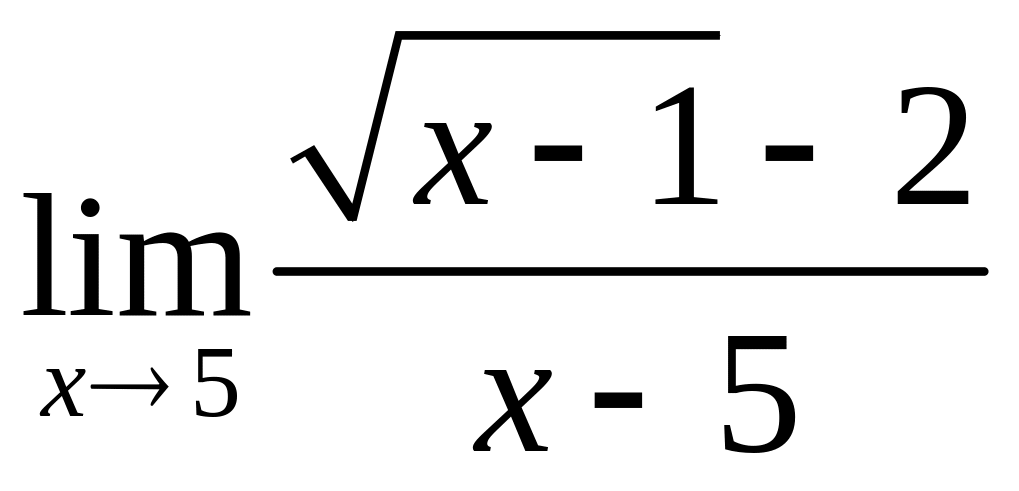 ,
б)
,
б)
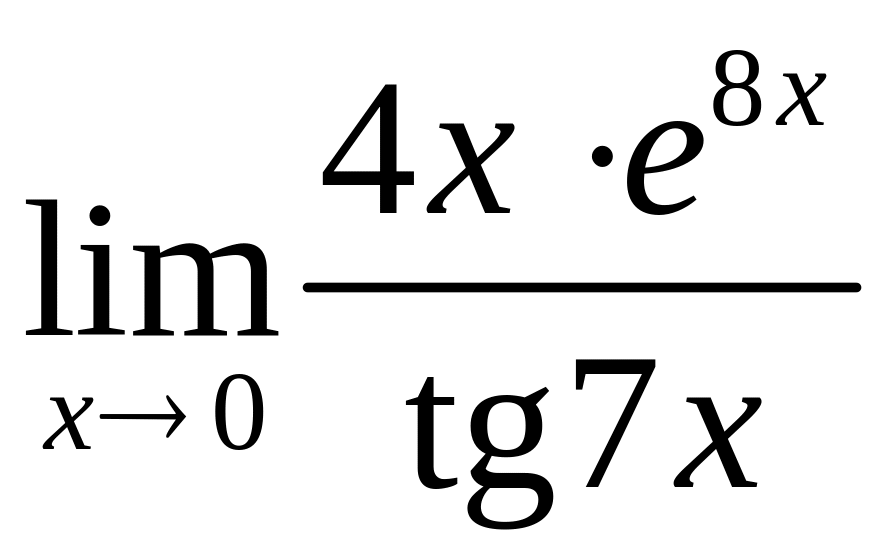 ,
в)
,
в)
![]() .
.
4.24. а)
![]() ,
б)
,
б)
 ,
в)
,
в)
![]() .
.
4.25. а)
 ,
б)
,
б)
![]() ,
в)
,
в)
 .
.
4.26. а)
 ,
б)
,
б)
 ,
в)
,
в)
![]() .
.
4.27. а)
![]() ,
б)
,
б)
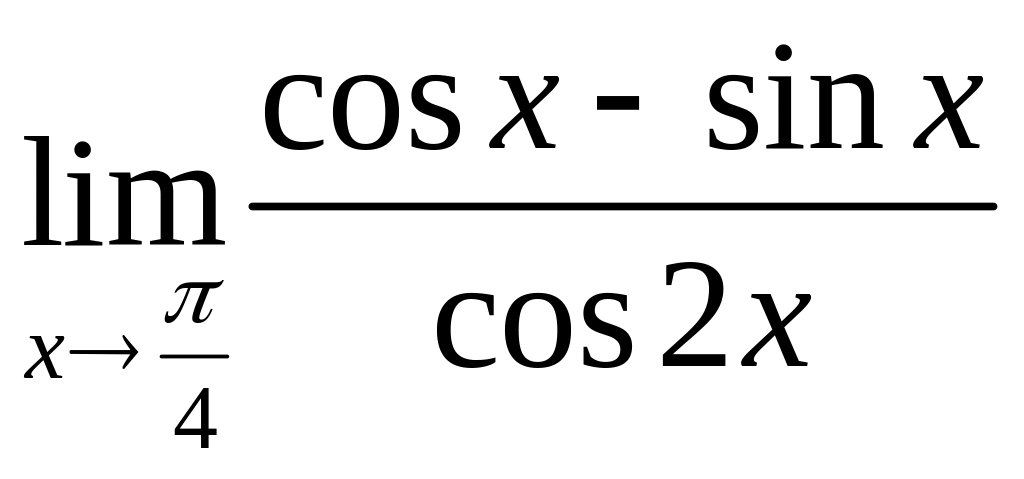 ,
в)
,
в)
![]() .
.
4.28. а)
 ,
б)
,
б)
![]() ,
в)
,
в)
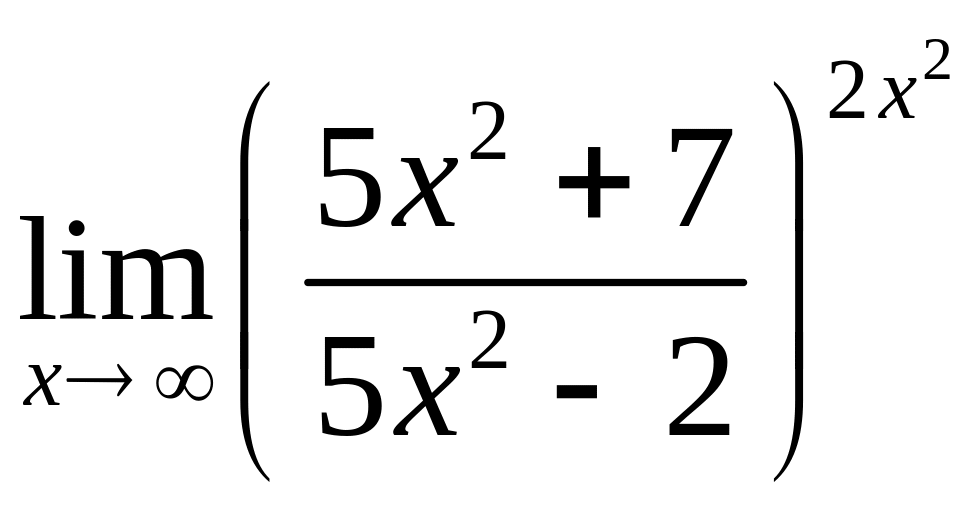 .
.
4.29. а)
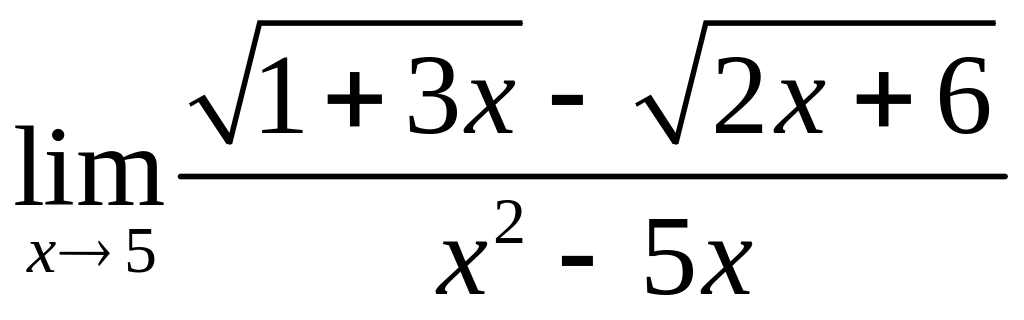 ,
б)
,
б)
 ,
в)
,
в)
![]() .
.
4.30. а)
 ,
б)
,
б)
![]() ,
в)
,
в)
![]() .
.
Задание
5.
Найти
производные
![]() .
.
5.1. а)
![]() ,
б)
,
б)![]() ,
в)
,
в)
![]() ,
г)
,
г)
 .
.
5.2. а)
![]() ,
б)
,
б)
 ,
в)
,
в)
![]() ,
г)
,
г)
![]() .
.
5.3. а)
![]() ,
б)
,
б)
 ,
в)
,
в)
![]() ,
г)
,
г)
 .
.
5.4. а)
![]() ,
б)
,
б)
 ,
в)
,
в)
![]() ,
г)
,
г)
![]() .
.
5.5. а)
![]() ,
б)
,
б) ,
в)
,
в)![]() ,
,
г)![]() .
.
5.6. а)
![]() ,
б)
,
б)
 ,
в)
,
в)
![]() ,
г)
,
г)
![]() .
.
5.7. а) ,
б)
,
б)
 ,
в)
,
в)
![]() ,
,
г)
![]() .
.
5.8. а)
![]() ,
б)
,
б)
 ,
в)
,
в)
![]() ,
,
г)
![]() .
.
5.9. а)
 ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
,
г)
![]() .
.
5.10. а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
г)
,
г)
![]() .
.
5.11. а)
![]() ,
б)
,
б)
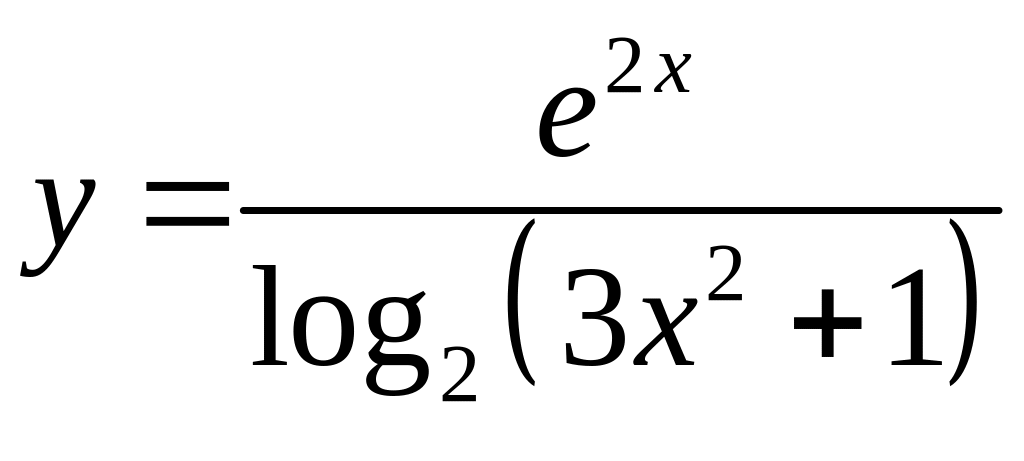 ,
в)
,
в)
![]() ,
г)
,
г)
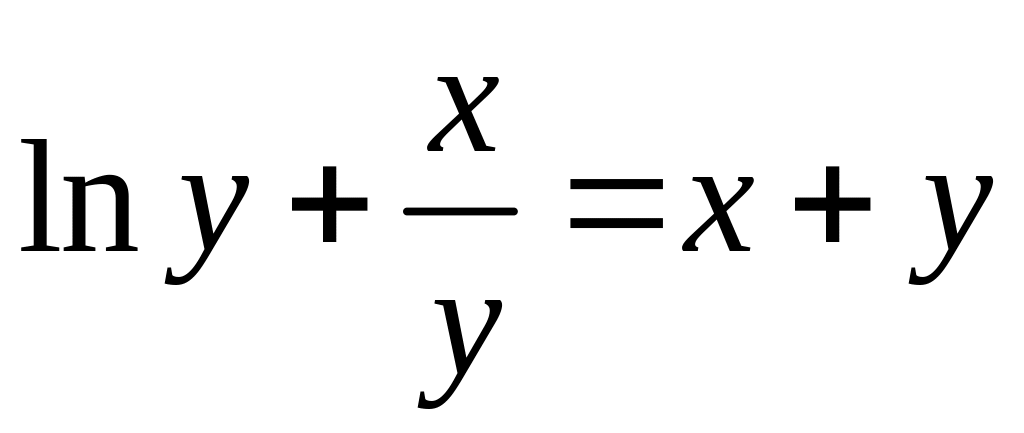 .
.
5.12. а)
![]() ,
б)
,
б)
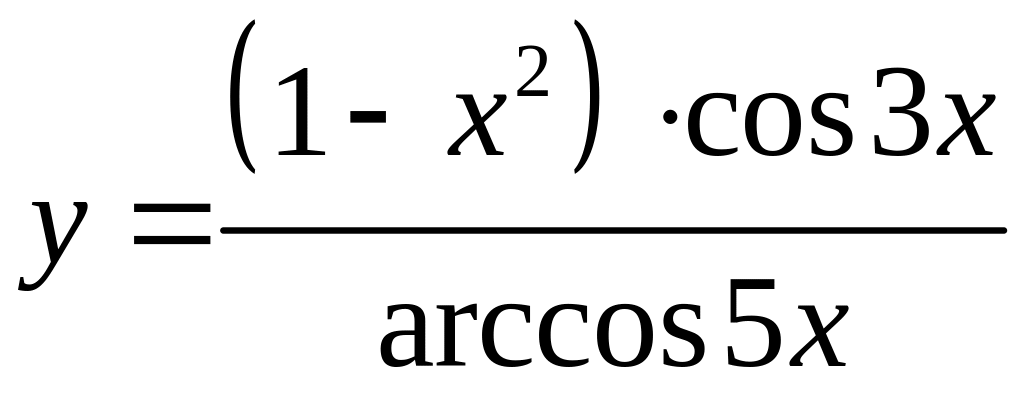 ,
в)
,
в)
![]() ,
,
г)
 .
.
5.13. а)
![]() ,
б)
,
б)
 ,
в)
,
в)
![]() ,
г)
,
г)
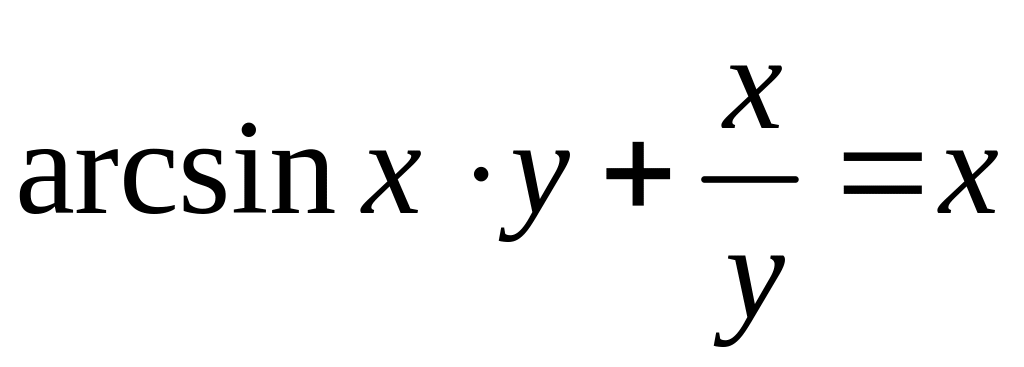 .
.
5.14. а)
![]() ,
б)
,
б)
![]() ,
в)
,
г)
,
в)
,
г)
![]() .
.
5.15. а)![]() , б)
, б) , в)
, в)
![]() ,
,
г)
![]() .
.
5.16. а)
![]() ,
б)
,
б)
 ,
в)
,
в)
![]() ,
,
г)
![]() .
.
5.17. а)
![]() ,
б)
,
б)
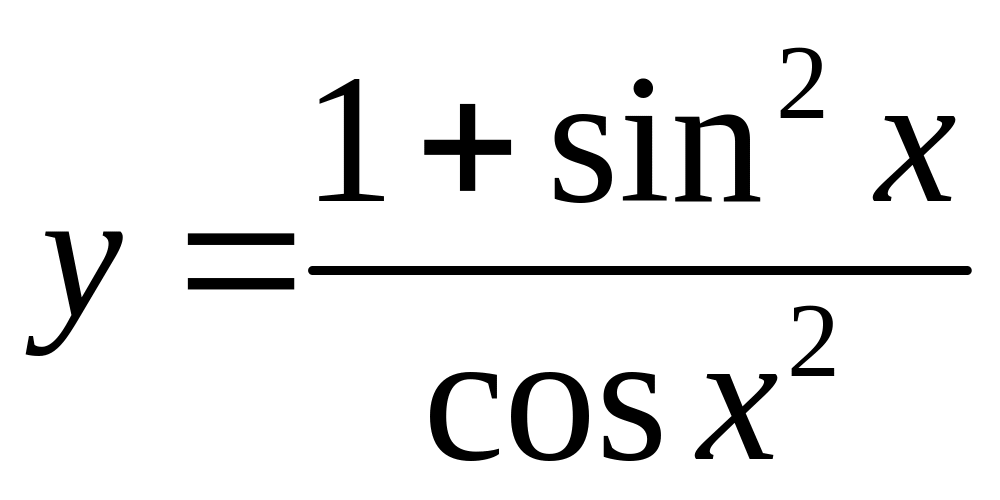 ,
в)
,
в)
![]() ,
,
г)
![]() .
.
5.18. а)![]() , б)
, б)![]() ,
в)
,
в)
![]() ,
г)
,
г)![]() .
.
5.19. а)![]() ,
б)
,
б)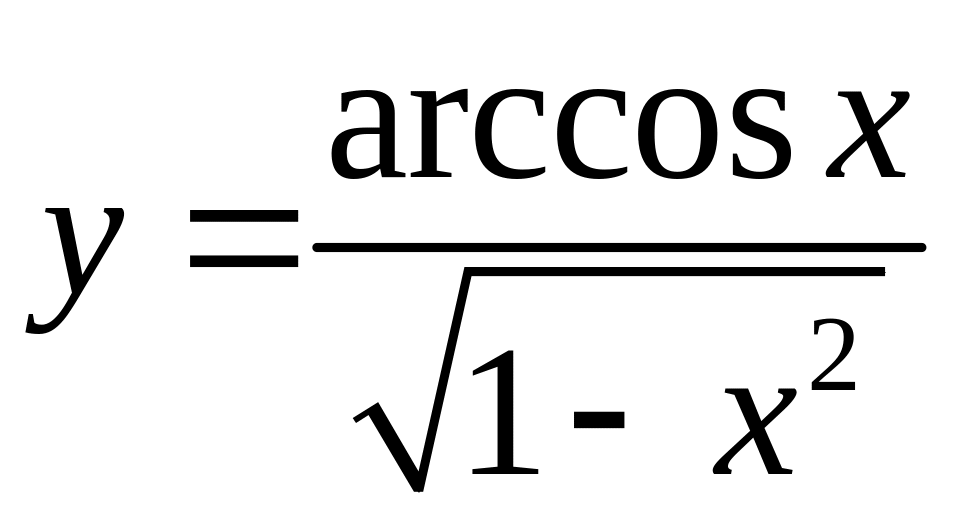 , в)
, в) ,
,
г)![]() .
.
5.20. а)![]() ,
б)
,
б)![]() ,
в)
,
в)![]() ,
,
г)![]() .
.
5.21. а) ,
б)
,
б)![]() ,
в)
,
в)![]() ,
,
г)![]() .
.
5.22. а)![]() ,
б)
,
б) ,
в)
,
в)![]() ,
г)
,
г)![]() .
.
5.23. а)
![]() ,
б)
,
б)
 ,
в)
,
в)
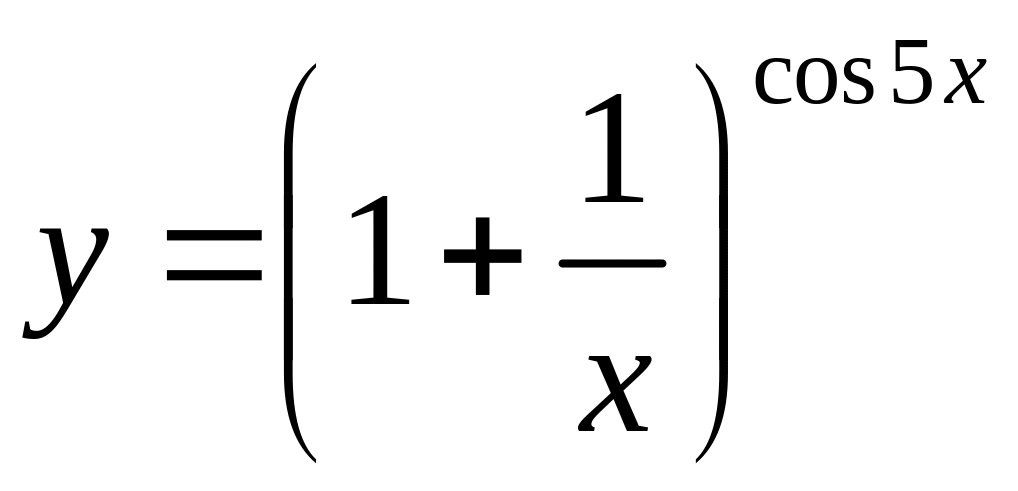 ,
г)
,
г)
![]() .
.
5.24. а)
![]() ,
б)
,
б)
 ,
в)
,
в)
![]() ,
,
г)
![]() .
.
5.25. а)
![]() ,
б)
,
б)
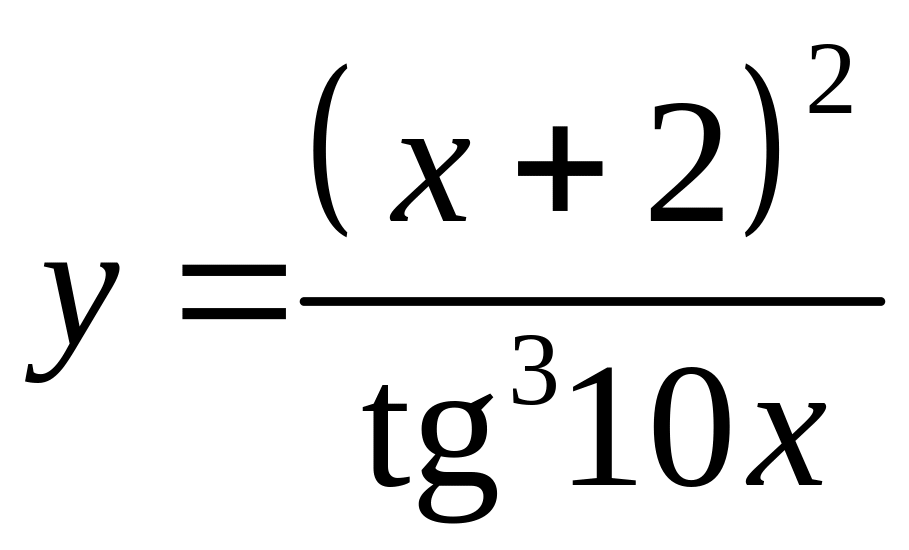 ,
в)
,
в)
![]() ,
г)
,
г)
![]() .
.
5.26. а)
![]() ,
б)
,
б)
 ,
в)
,
в)
 ,
г)
,
г)
![]() .
.
5.27. а)![]() ,
б)
,
б)![]() ,
в)
,
в)![]() ,
,
г)![]() .
.
5.28. а)
![]() ,
б)
,
б)
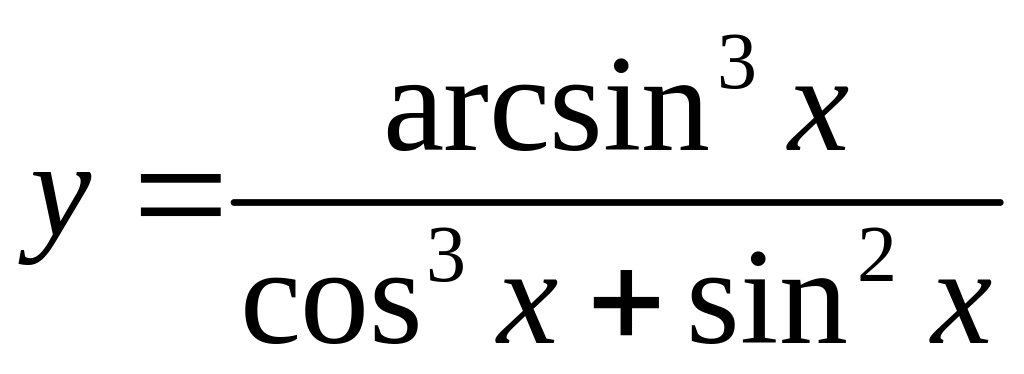 ,
в)
,
в)
![]() ,
,
г)
![]() .
.
5.29. а)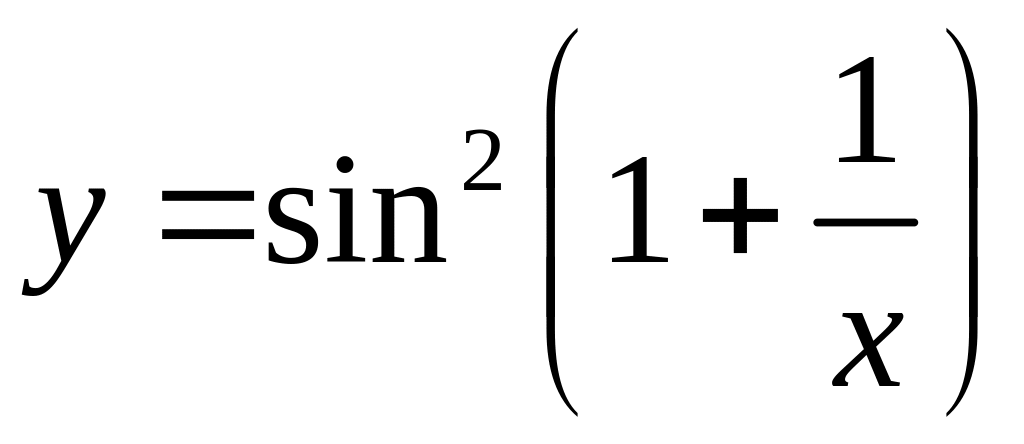 ,
б)
,
б)![]() ,
в)
,
в)![]() ,
,
г)![]() .
.
5.30. а)
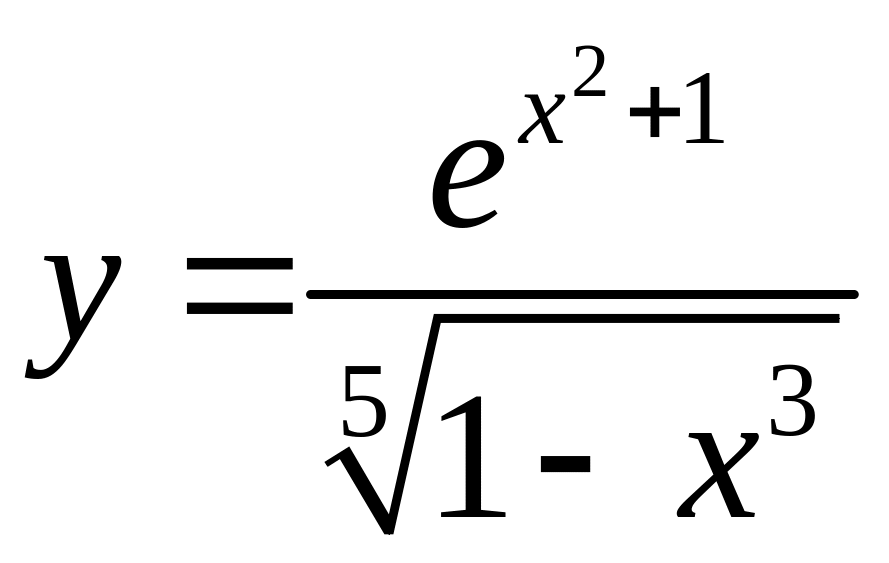 ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
г)
,
г)
![]() .
.
Задание 6. Найти производные второго порядка для параметрической функции.
6.1.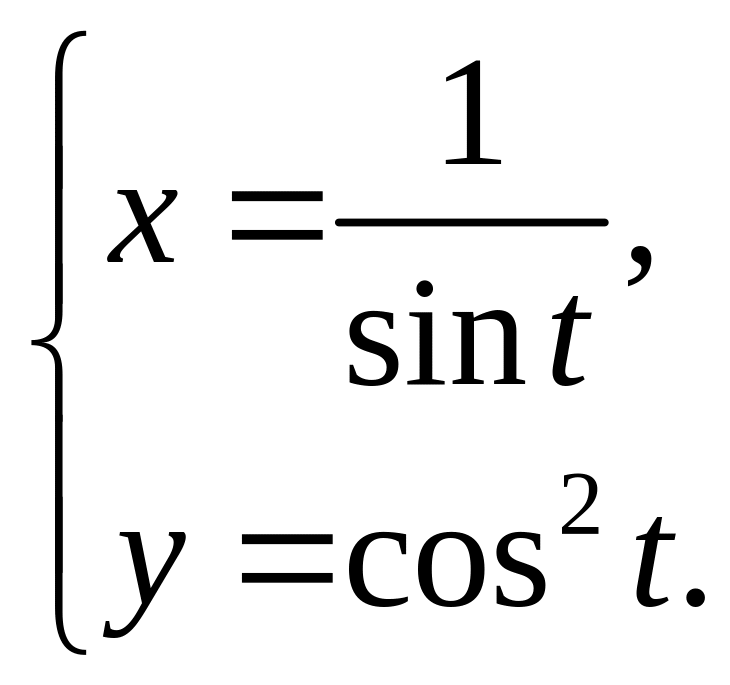 6.2.
6.2. 6.3.
6.3. 6.4.
6.4.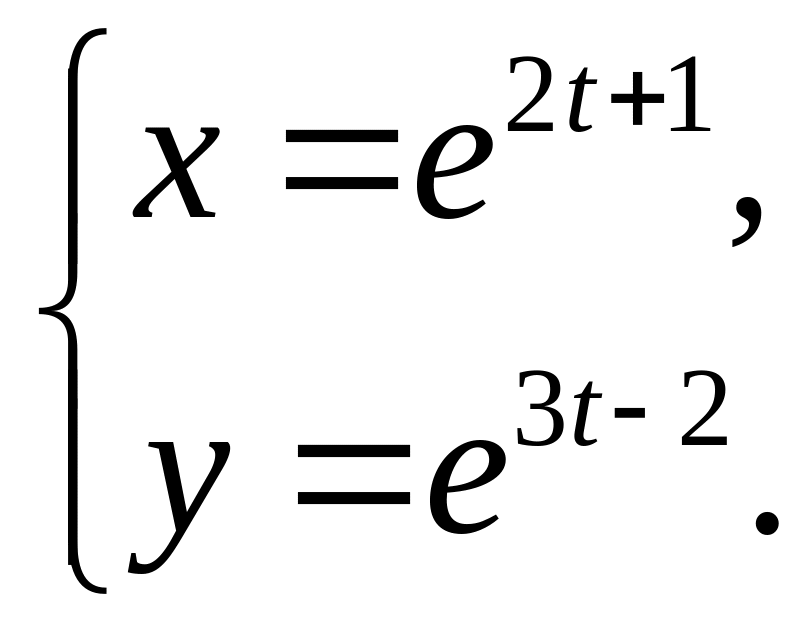
6.5. 6.6.
6.6.
 6.7.
6.7.
 6.8.
6.8.
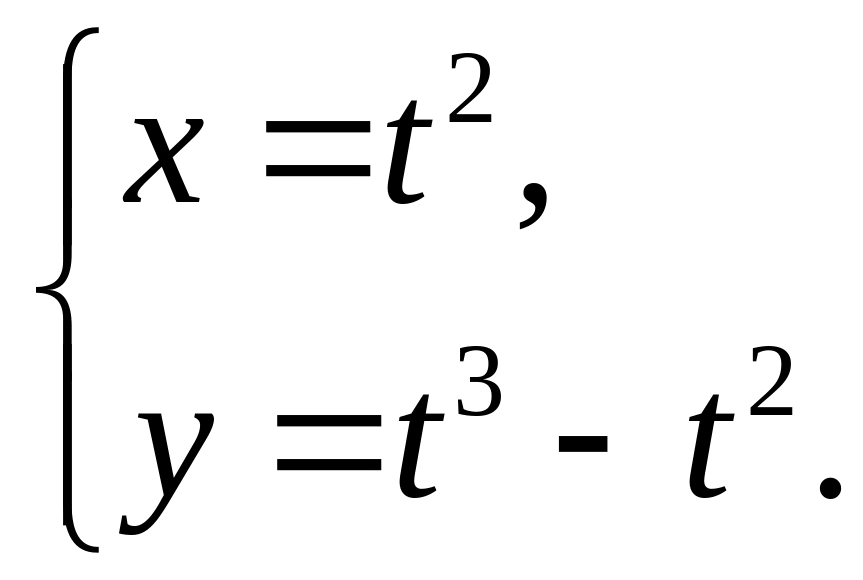
6.9. 6.10.
6.10. 6.11.
6.11.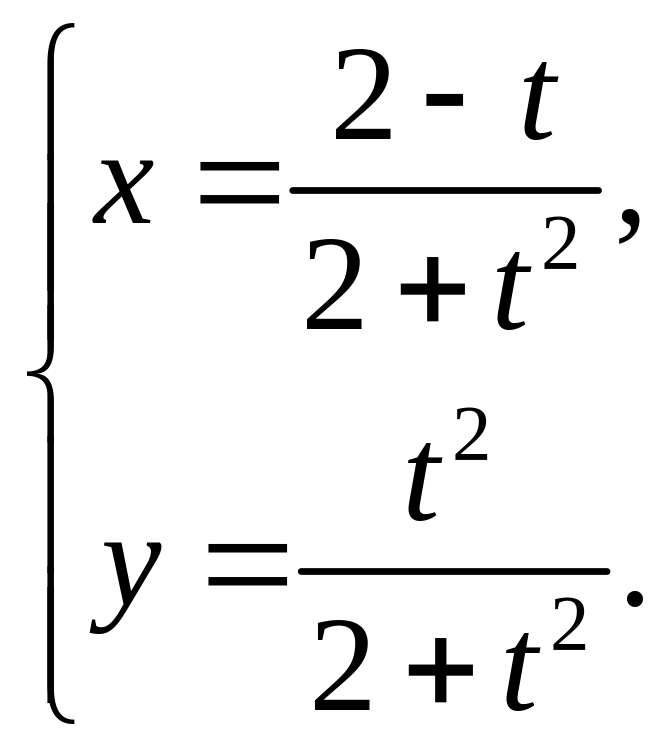 6.12.
6.12.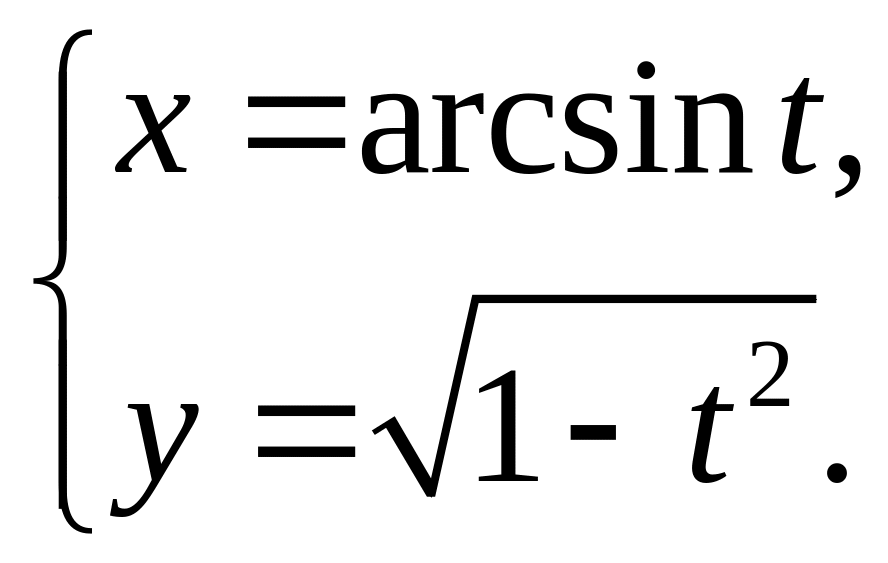
6.13. 6.14.
6.14. 6.15.
6.15. 6.16.
6.16.
6.17. 6.18.
6.18. 6.19.
6.19.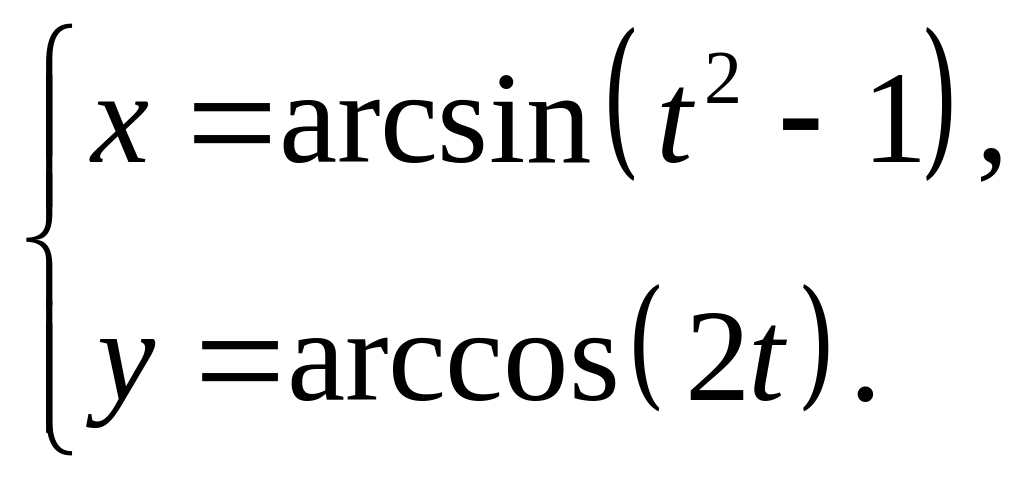
6.20.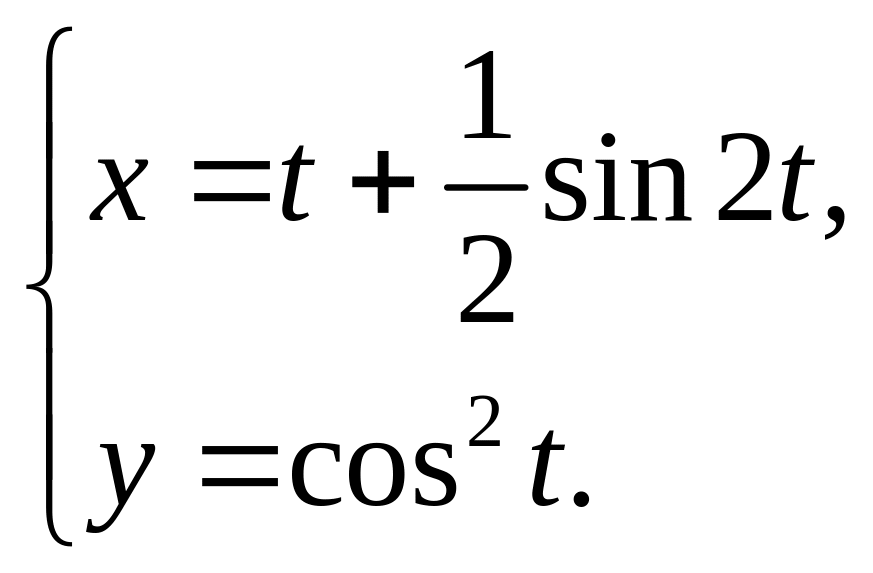 6.21.
6.21. 6.22.
6.22.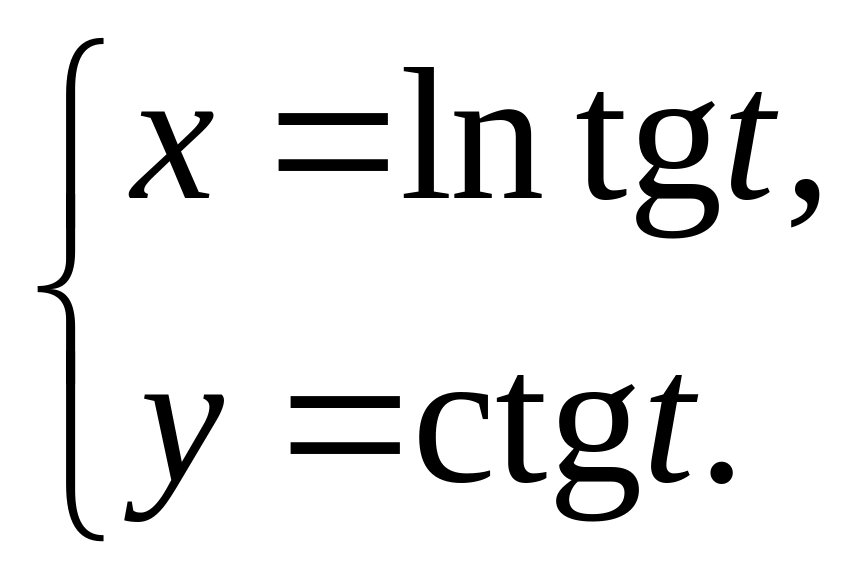
6.23.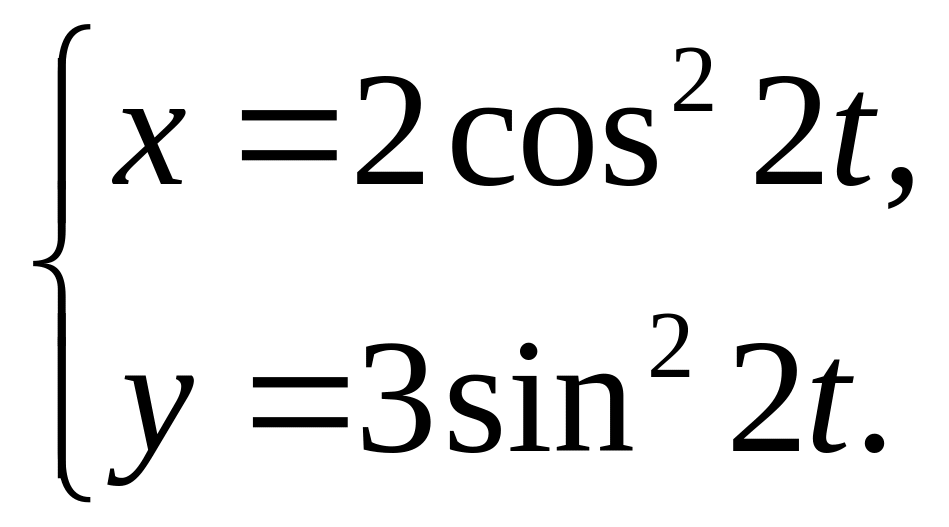 6.24.
6.24. 6.25.
6.25.
6.26.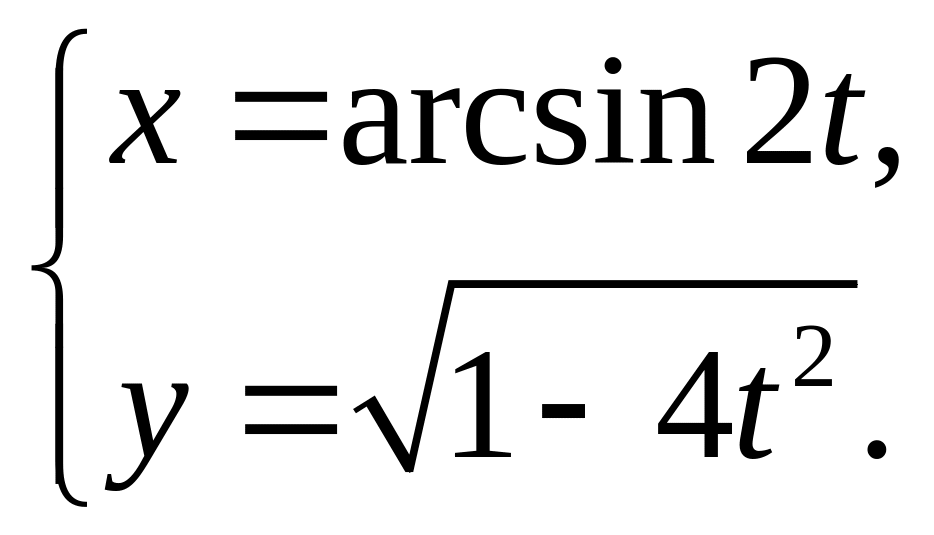 6.27.
6.27. 6.28.
6.28.

6.29.
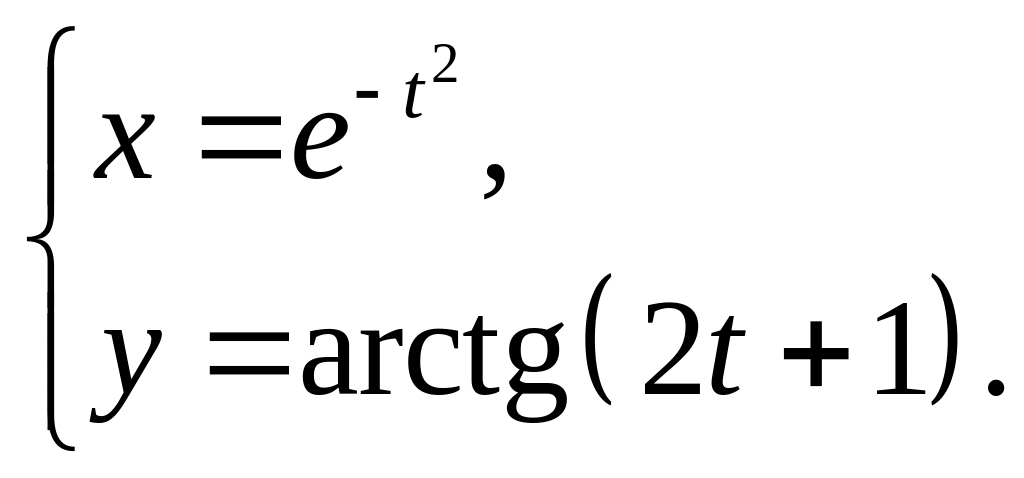 6.30.
6.30.
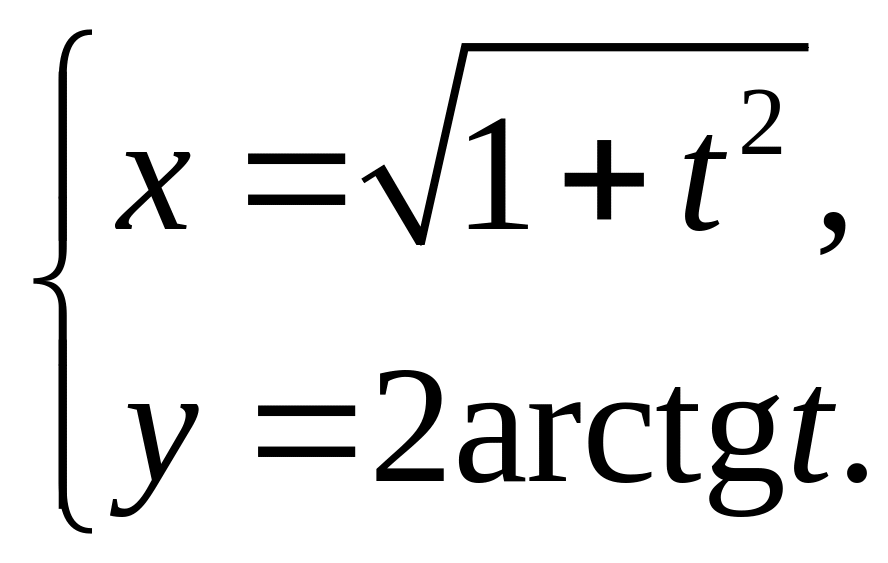
Задание
7.
Исследовать
функцию
![]() и построить ее график.
и построить ее график.
7.1.
![]() .
7.2.
.
7.2.
![]() .
7.3.
.
7.3.
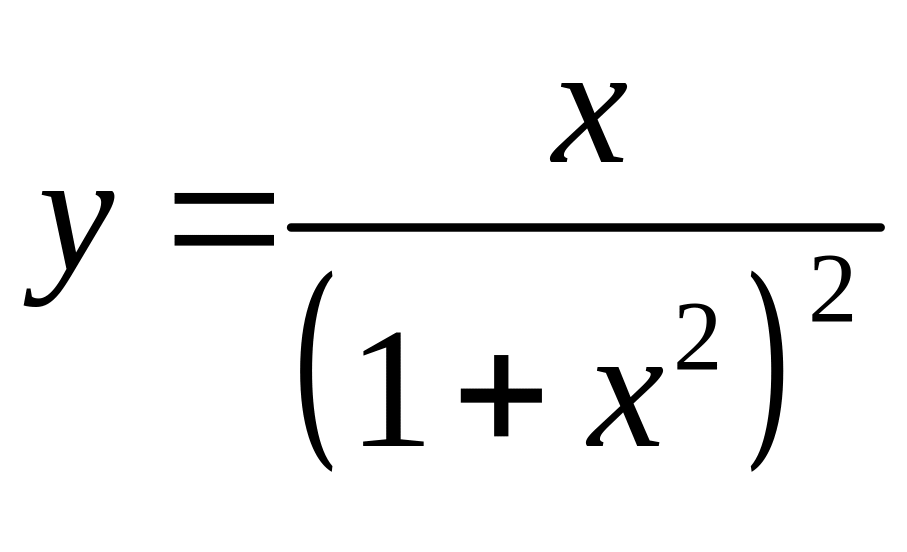 .
7.4.
.
7.4.
![]() .
.
7.5.
 .
7.6.
.
7.6.
 .
7.7.
.
7.7.
![]() .
7.8.
.
7.8.
![]() .
.
7.9.
![]() .
7.10.
.
7.10.
 .
7.11.
.
7.11.
![]() .
7.12.
.
7.12.
![]() .
.
7.13.
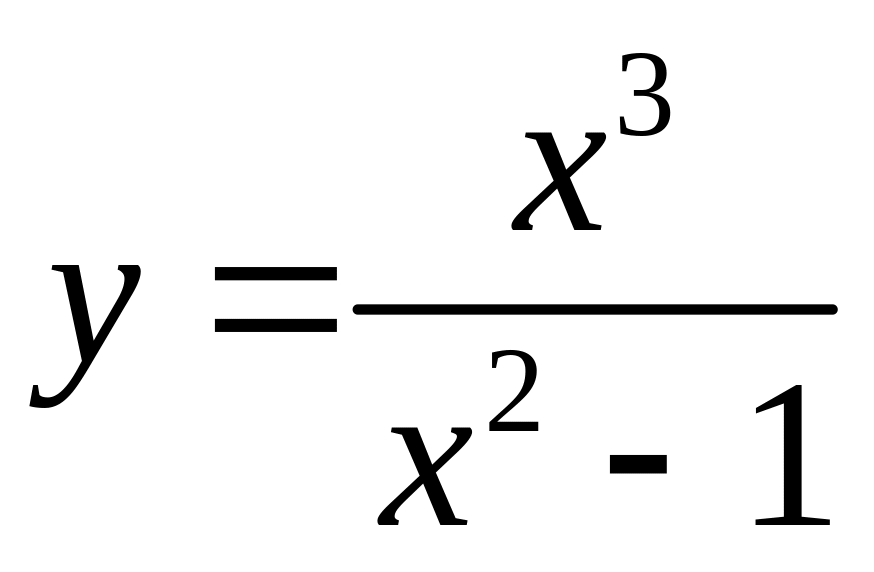 .
7.14.
.
7.14.
![]() .
7.15.
.
7.15.
![]() .
.
7.16.
 .
7.17.
.
7.17.
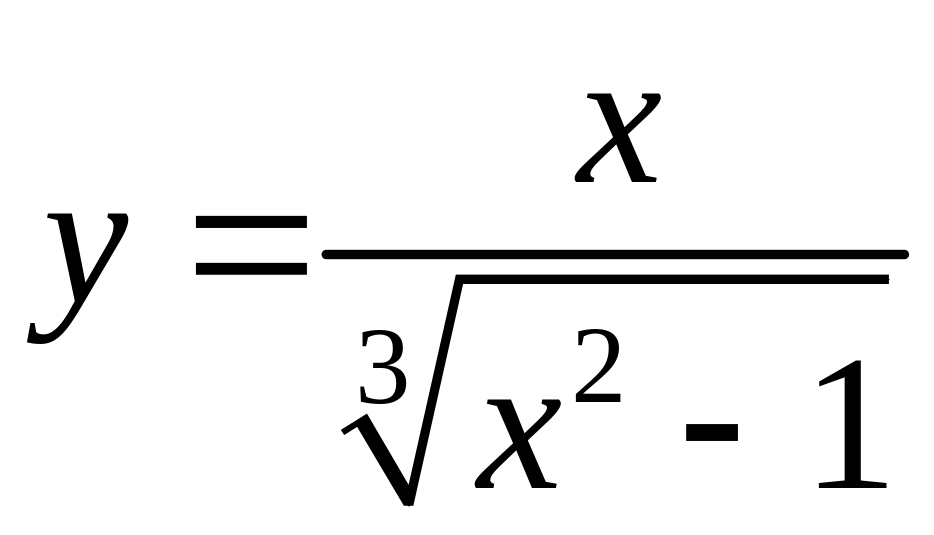 .
7.18.
.
7.18.
 .
.
7.19.
 .
7.20.
.
7.20.
 .
7.21.
.
7.21.
![]() .
.
7.22.
![]() .
7.23.
.
7.23.
![]() .
7.24.
.
7.24.
![]() .
.
7.25.
![]() .
7.26.
.
7.26.
![]() .
7.27.
.
7.27.
![]() .
.
7.28.
![]() .
7.29.
.
7.29.
 .
7.30.
.
7.30.
![]() .
.
