Тема 3. Введение в математический анализ. Дифференциальное исчисление функции одной переменной
1. Понятие числовой последовательности и ее предела.
2. Предел функции в точке. Основные теоремы о пределе суммы, произведения и частного.
3. Замечательные пределы.
4. Непрерывность функции в точке. Точки разрыва и их классификация.
5. Понятие производной, ее геометрический смысл.
6. Производная суммы, произведения, частного.
7. Дифференциал и его геометрический смысл.
8. Производная функции, заданной неявно и параметрически.
9. Производные и дифференциалы высших порядков.
10. Возрастание и убывание графика функции. Экстремум.
11. Выпуклость и вогнутость функции. Точки перегиба.
12. Наибольшее и наименьшее значения функции на отрезке.
3.1. Предел функции. Основные способы вычисления пределов
Число А
называют пределом
функции
при
(или в точке а),
если для любого числа
существует такое число
,
что при всех х,
удовлетворяющих условию
,
выполняется неравенство
.
Обозначают предел
.
Если функции
и
имеют пределы в точке
,
то:
,
,
.
Функция
называется бесконечно
малой в точке
,
если ее предел в этой точке равен нулю:
.
Функция
называется бесконечно
большой в
точке
,
если для любого числа
существует такое число
,
что для всех х,
удовлетворяющих неравенству
,
выполняется неравенство
.
При этом записывают
.
При нахождении
предела
в случае, когда
и
являются бесконечно малыми (бесконечно
большими) функциями в точке
,
говорят, что отношение
при
представляет собой неопределенность
вида
.
Аналогично вводятся
неопределенности вида
,
,
,
,
,
которые встречаются при нахождении
соответственно пределов
и
.
Отыскание предела в таких случаях
называют раскрытием неопределенности.
При решении задач используют:
а) первый замечательный предел:
;
б) второй замечательный предел:
или
;
в) некоторые важные пределы:
, 
,
, 
.
г) эквивалентность бесконечно малых функций.
Пусть
и
бесконечно малые функции в точке
.
Если
,
то
и
называются эквивалентными бесконечно
малыми функциями, что обозначается так:
.
Т е о р е м а. Предел отношения двух бесконечно малых функций при не изменится, если каждую из них или только одну заменить другой эквивалентной бесконечно малой функцией.
При замене бесконечно малой функции эквивалентной используют таблицу эквивалентных бесконечно малых функций при :
1.
; 2.
; 3.
(х)
;
4.
; 5.
; 6.
.
Рассмотрим основные
методы раскрытия неопределенностей
.
Пример 3.1.
Вычислить
.
Решение.
Имеем неопределенность
.
Преобразуем выражение под знаком предела:
.
Пример 3.2.
Вычислить
.
Пример 3.3.Вычислить
.
Решение.
Имеем неопределенность
.
Выделим в числителе и в знаменателе
одинаковый множитель
.
Для этого разложим числитель и знаменатель
на сомножители. Имеем:
.
Пример 3.4.Вычислить
.
Решение.
Имеем неопределенность
.
Умножаем числитель и знаменатель на
сопряженное выражение
:
.
Пример 3.5.
Вычислить
.
Решение.
Имеем неопределенность
.
Используем первый замечательный передел.
В нашем случае
,
.
Следовательно,
получаем
.
Пример 3.6.
Вычислить
.
Решение.
Имеем неопределенность
.
Заменим бесконечно малую функцию
при
эквивалентной бесконечно малой функцией
.
Получаем
.
Неопределенности
вида
и
преобразуются к неопределенности
вида
.
Пример 3.7.
Вычислить
.
Решение. Имеем неопределенность вида . Приведем две дроби к общему знаменателю:
.
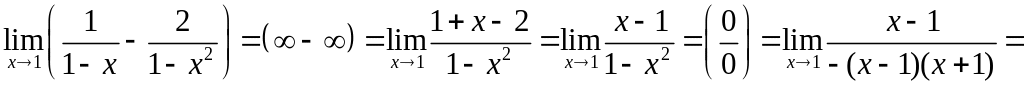
Пример 3.8.
Вычислить
.
Решение. Имеем неопределенность вида . Преобразуем выражение:
=
.
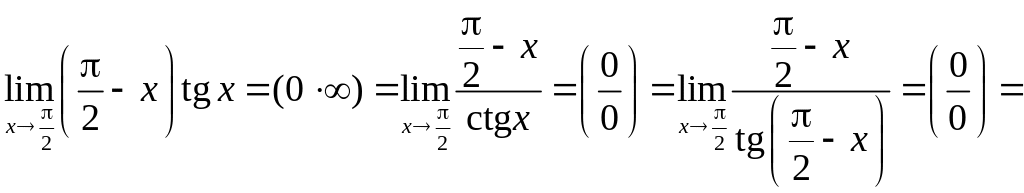
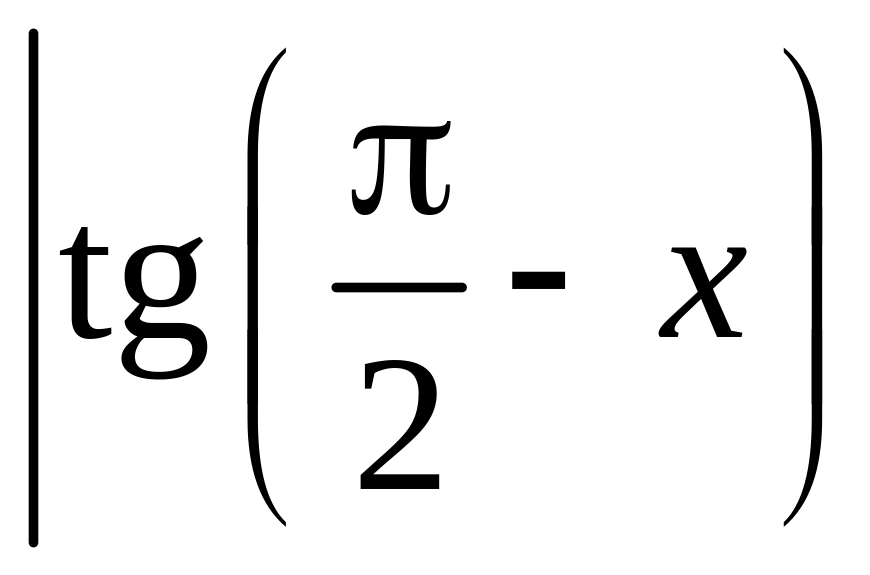
Для раскрытия
неопределенности вида
применяют второй замечательный
предел. Пусть
,
а
.
Тогда имеем
.
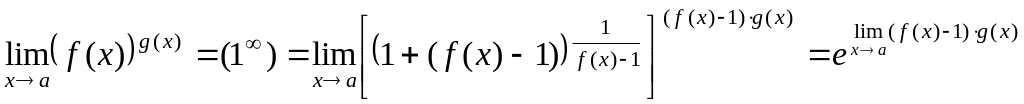Приходим к неопределенности вида .
Пример 3.9. Вычислить
.
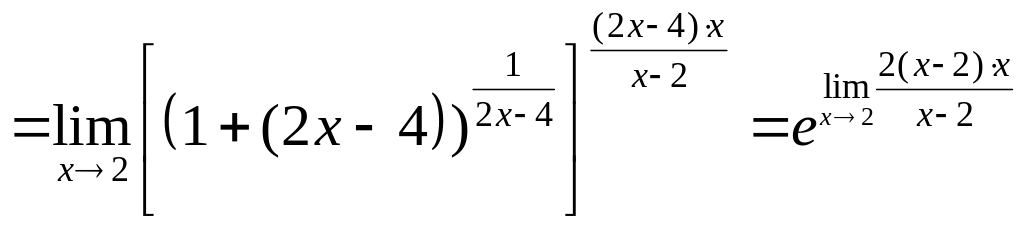
Пример 3.10. Вычислить
.
Производной
функции
в точке
называется предел отношения приращения
функции к приращению аргумента при
условии, что приращение аргумента
стремится к нулю:
.
Операция нахождения производной называется дифференцированием.
Если функции
и
и имеют производные в некоторой точке
х
, то основные
правила дифференцирования
выражаются формулами:
; 
;
; 
; 
,
.
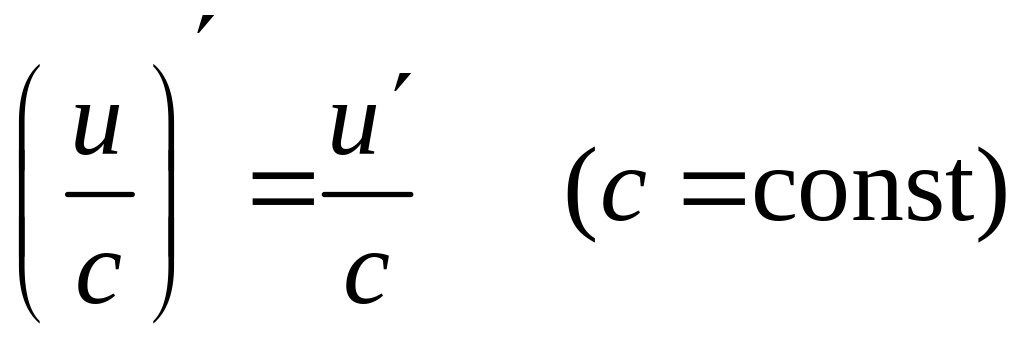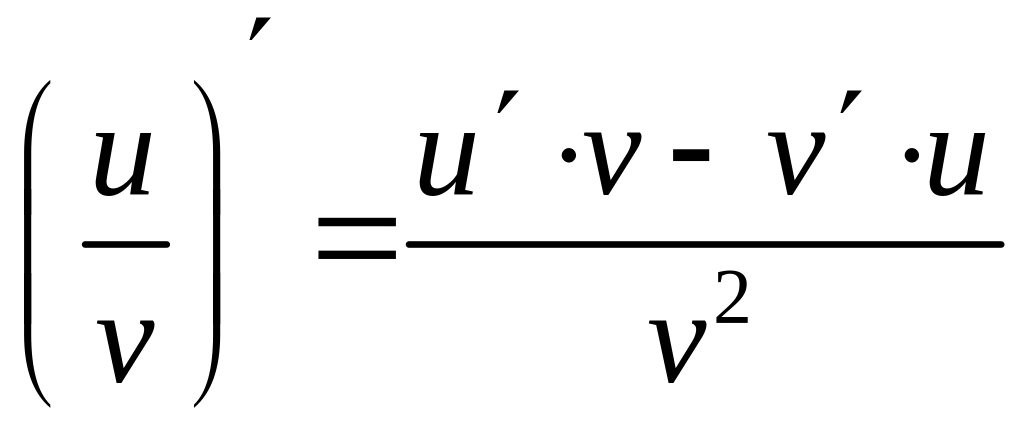Таблица основных производных
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
