3.3.3. Выбор более (менее) точных методов и си

Для этих целей следует использовать рекомендации РМГ 64-2003 [9]. Основные способы следующие.

1. Замена СИ на более точное. Способ целесообразен в случае доминирования инструментальной составляющей погрешности измерений.

2. Выбор СИ с таким верхним пределом, чтобы ожидаемое значение измеряемой величины находилось в последней части диапазона. Способ целесообразен в случае, когда нормируется приведенная погрешность СИ и приводит к уменьшению относительной инструментальной погрешности. Имеем

, , отсюда ,

где – нормирующее значение измеряемой величины – верхний предел или диапазон измерений СИ.

Например, допустим, что весы имеют приведенную погрешность, равную 1%, и верхний предел измерений – 10 кг. Если измеряется масса порядка 3 кг, то получим результат измерений с относительной погрешностью, равной

.

Если измеряется масса порядка 8 кг, то получим результат измерений с относительной погрешностью, равной

.

Таким образом, удалось уменьшить относительную инструментальную погрешность практически в 3 раза.

3. Ограничение условий применения СИ. Способ целесообразен, когда доминируют дополнительные погрешности. Следует использовать специальные меры, снижающие влияние воздействующих величин (кондиционеры, обогреватели, экранирование, амортизаторы и т.д.).

4. Выполнение многократных наблюдений с последующим усреднением результатов. Способ эффективен при доминировании случайной составляющей погрешности.

По результатам N проведенных наблюдений можно получить:

• в качестве результата измерений – среднее арифметическое N наблюдений ;

• в качестве оценки погрешности отдельного наблюдения – стандартное отклонение ;

• в качестве оценки случайной составляющей погрешности результата измерений – стандартное отклонение среднего значения .

Таким образом, результат измерений запишем в виде , а сам способ позволяет уменьшить случайную составляющую погрешности результата измерений в раз.

5. Автоматизация измерительных процедур. Мероприятие способствует исключению субъективных погрешностей.

6. Использование методов сравнения с мерой. Способ целесообразен, когда доминирует методическая составляющая погрешности измерений и приводит к уменьшению систематической составляющей погрешности измерений (это составляющая при каждом измерении остается, как правило, неизменной). Известны такие методы сравнения с мерой, как дифференциальный, нулевой и метод замещения.

В рамках дифференциального метода на СИ воздействует разность измеряемой величины и известной величины, воспроизводимой мерой. При этом величины должны незначительно отличаться друг от друга.

Допустим, что необходимо измерить напряжение некоторого источника, значение которого составляет порядка U_x ≈ 0,95 В. Имеются вольтметры V1 и V2 с пределами измерений 1,0 и 0,1 В соответственно. Приведенная погрешность обоих СИ составляет 1%. Также в наличии есть образцовая мера напряжения U_m ≈ 1,0 В, погрешность которой мала.

Рассмотрим два варианта измерения напряжения неизвестного источника.

Вариант 1 – используем вольтметр V1. Если измерить напряжение U_x непосредственно этим вольтметром, то получим результат с абсолютной погрешностью, равной 1 % от 1,0 В, т.е. – 0,01 В (см. левую часть рисунка 5).

Вариант 2 – используем вольтметр V2 и меру U_m. Если измерить разность напряжений вольтметром V2 (соединить источник и меру встречно), то абсолютная погрешность результата измерений будет равна 1 % от 0,1 В, т.е. – 0,001 В (см. правую часть рисунка 5). Таким образом, удается уменьшить погрешность результата измерений в 10 раз.

Рисунок 5 – Варианты соединения источника напряжения и вольтметра

При использовании нулевого метода результирующий эффект воздействия измеряемой величины и меры на устройство сравнения доводят до нуля, например, при измерении массы на рычажных весах (см. рисунок 6).

Рисунок 6 – Измерение массы на рычажных весах – пример нулевого

метода измерений

Метод замещения – это метод, в котором измеряемую величину замещают мерой с известным значением. Причем сравнение с мерой производят разновременно. Наиболее известным методом этой группы является способ Борда – взвешивание с поочередным помещением измеряемой массы и гирь на одну и ту же чашку весов.

Шаг 1. На одну из чашек помещают измеряемую массу m_x и весы уравновешивают гирями.

Шаг 2. На той же чашке весов вместо измеряемой массы размещают известную массу m_о (мера, гиря) и весы уравновешивают гирями вновь.

Шаг 3. К значению меры следует прибавить величину, на которую изменилось показание весов на первом и втором шагах, получим

.

Таким образом, удается повысить точность измерений за счет отсутствия погрешности из-за неточности гирь и несимметричности плеч весов, ведь положение равновесия на рычажных весах характеризуется выражением (рисунок 7):

,

где m_x, m_г – значения массы взвешиваемого тела и гирь; L₁, L₂ – длины плеч рычагов весов.

Рисунок 7 – Симметричность рычажных весов

7. Использование информационной избыточности, возникающей в случае, когда количество измерительной информации больше минимально необходимого значения.

Например, для измерения некоторой величины используем несколько одинаковых СИ с последующим усреднением их показаний (см. рисунок 8). Если все СИ имеют одинаковую относительную погрешность , то результат измерений и полученная погрешность будут равны

, .

Рисунок 8 – Измерение несколькими СИ – пример информационной

избыточности

Таким образом, результат измерений запишем в виде , а сам способ позволяет уменьшить относительную погрешность результата измерений в раз.

Если N СИ имеют различные относительные погрешности , то результат измерений и полученная погрешность будуь равны

, .
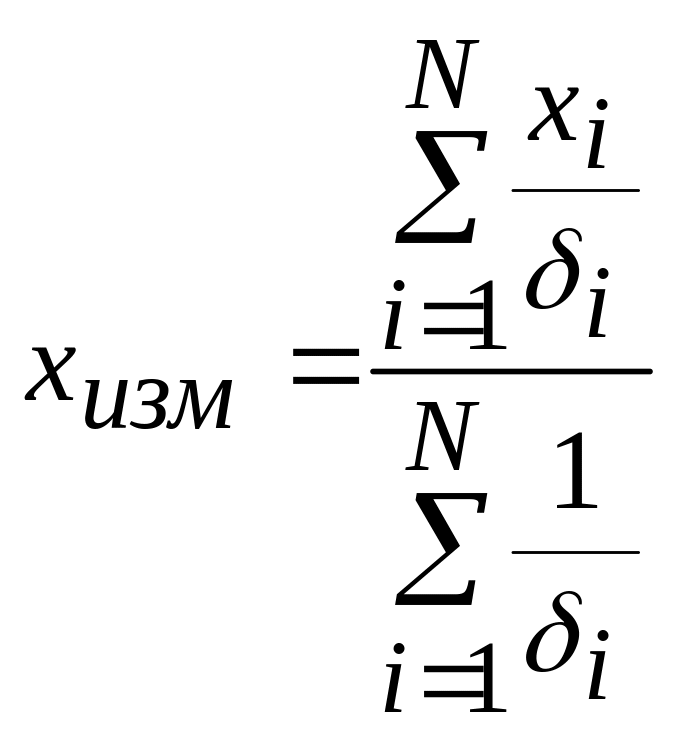