Оскільки довжини ходів різні, то виміри будуть нерівноточними.

Обчислюємо ваги вимірів за формулою

і заносимо в графу 4 таблиці.

Для визначення середнього арифметичного використаємо формулу:

= ........................

де ............................. ; (графа 5)

....................... ; [P] = ...................... ; = .......................... .

Обчислюємо ймовірні похибки і заносимо в графу 7.

В графі 8 обчислюємо добутки та їх суму = ..................................... .

Обчислюємо: - середню квадратичну похибку одиниці ваги за формулою

= ................................... ;

• середні квадратичні похибки кожного виміру за формулою 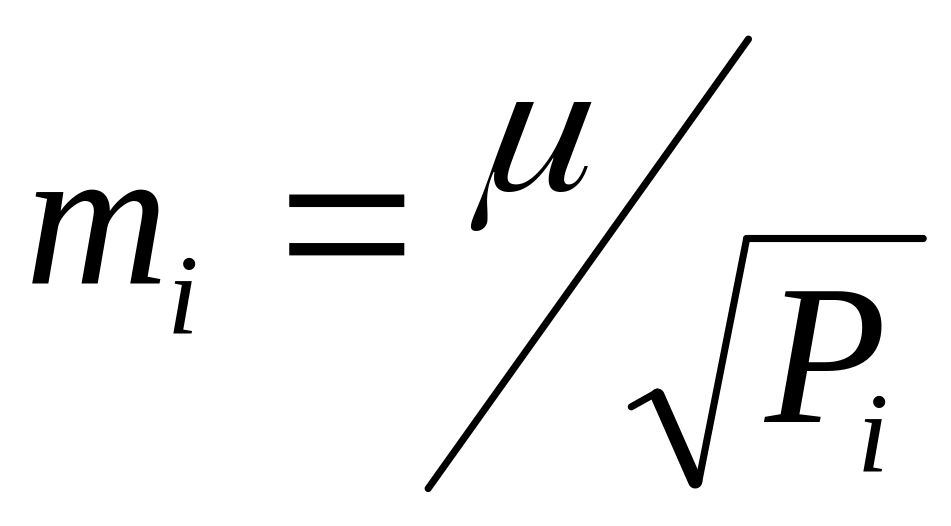і вносимо в графу 9;

• середню квадратичну похибку загального середнього арифметичного

.................... = ;

• с.к.п. с.к.п. одиниці ваги

= ................... ;

• с.к.п. с.к.п загального середнього арифметичного

= ................... .

Виконуємо інтервальну оцінку.

По таблицям розподілу Ст’юдента визначаємо параметр t при Р = 0,90 та n – 1 = 6 – 1 = 5

t = ..................................... .

Визначаємо інтервал для істинного значення позначки точки

...................................................................

Для прикладу визначимо інтервал для другого виміру

де - взято в строчці 2 графи 9 таблиці .......... .

Визначаємо інтервал для стандарту загального середнього арифметичного.

По таблицям розподілу Пірсона (додаток ) визначаємо значення = ............. ; = ....................... ; при та

при n = 6 – 1 = 5.

Обчислюємо коефіцієнти

.............................. ; ........................ .

Тоді ;

.......................................................... .

Інтервал значення позначки для і-го хода визначається за формулою:

......... .............. .

Оцінка точності функцій. Розрахунок точності вимірів

Завдання 13. (Приклади 28,33). Для функцій, наведених у табл.6:

1. обчислити їх середні квадратичні похибки;

2. за принципом рівного впливу обчислити середні квадратичні похибки аргументів (вимірювань) при заданій с.к.похибці функції (табл.6, графа 5).

Вихідні дані: Таблиця 6.

Таблиця 6

№№ п\п	Назва функції	Функція	Вихідні дані	С.к.п. функцій
1	2	3	4	5
1 2	Обчислення перевищення між точками		м мм 2 мм	мм
3 4	Обчислення поправки за приведення лінії до горизонту		м мм м мм	мм
5 6	Обчислення горизонтального прокладання лінії		Дані взяти із пунктів 3 і 4	10 мм
7 8	Обчислення приростків координат		м мм	20 мм

Розв’язання:

1. Функція

а) Визначення с.к.похибки функції

Визначаємо похідні

= ......................................................................... .

= .............................................. .

Дисперсія визначається за формулою:

.

Тоді ,

або .

= ................................................ .

С.к.похибки функції = ...................................... .

Значення = 206265 використовується для переведення другого члена формули до лінійної розмірності.

б) Визначення с.к.похибок аргументів функції, коли = ................. (таблиця 6 графа 5).

Приймаємо:

Маємо

Тоді , а ................ .

Обчислюємо с.к.похибки аргументів

= ............................. ; = ............................. .

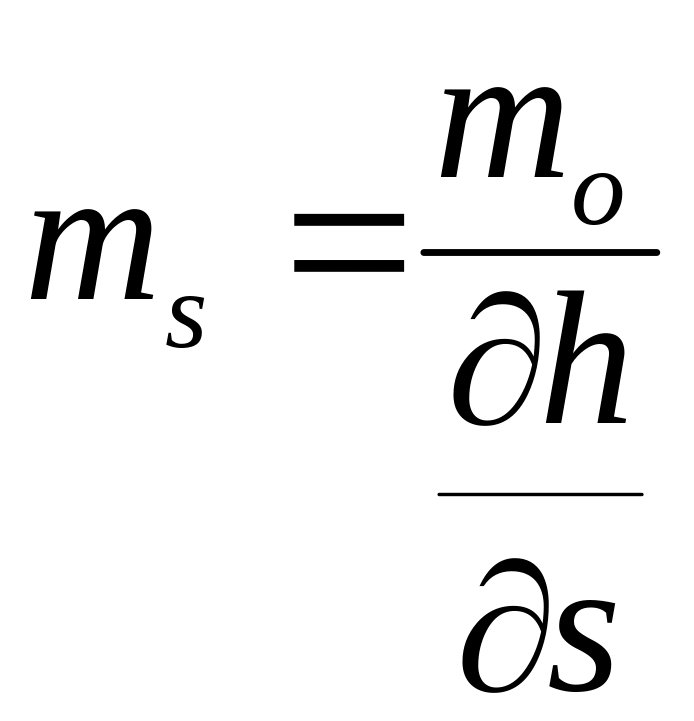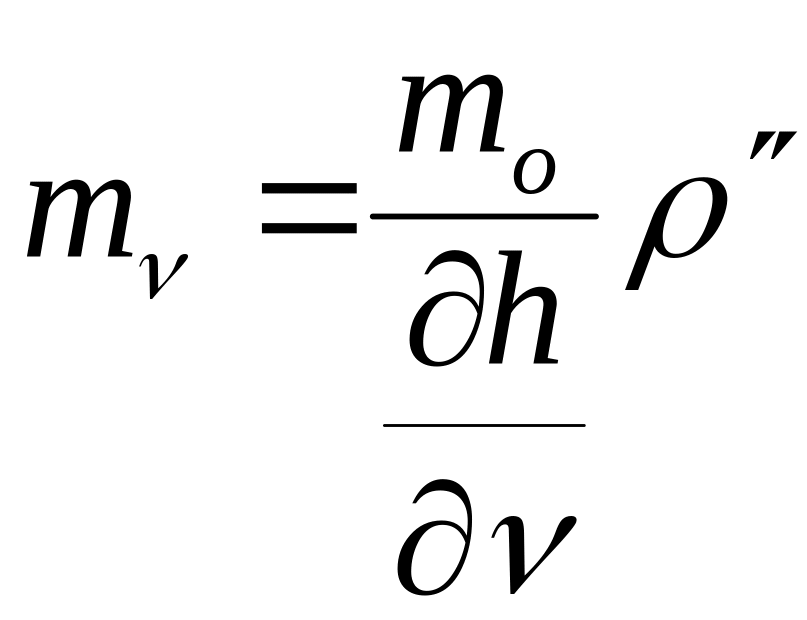2. Функція

а) Визначаємо похідні

...................... = ..........................

....................... = ............................

+ 1 ; - 1

Дисперсія та середня квадратична похибка функції

= .................................................. ;

.......................................... = ............................ .

Приймаємо ......................................................................................................................................

...........................................................................................................................................................

Тоді = ........................................., а ............................. .

С.к.похибки аргументів:

= ...................... = .................; = .......................... = .................. .

= ...................... = ................ ; = .......................... = ................... .

3. Функція .

а) Визначаємо похідні

....................... = ....................... .

.......................... = .................... .

Дисперсія та с.к.похибки функції дорівнюють:

= .....................................................................= ........................ .

.............................................................................. = ........................................ .

б) Визначення с.к.п. аргументів, коли с.к. похибка функції = ...................(табл.6, графа5)

Приймаємо ..........................................................................................................................................

..............................................................................................................................................................

Тоді = .......................................... , а .......................................... .

С.к.похибки аргументів

= ..................=....................... ; = ..............................= ................................ .

4. Функція

а) Визначаємо похідні

............................. = ................................................... .

............................. = ..................................................... .

Дисперсія та с.к. похибка функції

= .......................................................................................

.............................................................................. = ................................. .

б) Визначення с.к.похибок аргументів коли с.к. похибки функції = ...................(табл.6,графа5)

Приймаємо ..........................................................................................................................................

..............................................................................................................................................................

Тоді = ................................... , а

С.к.похибки аргументів

= .....................=.......................... ; = ................................. = ....................... .

5. Функція

а) Визначаємо похідні

....................................... = .......................................... .

......................................= .......................................... .

Дисперсія та с.к.п. функції

= ................................................................................................................................

.......................................................... = ......................................................................... .

б) Визначення с.к.похибок аргументів коли с.к.похибка функції ................. (табл.6, графа 5).

Приймаємо ......................................................................................................................................

...........................................................................................................................................................

Тоді = ............................................ ; а .................................. .

С.к.похибки аргументів

..................................... ; = ..................................... .

6. Функція

а) Визначаємо похідні

..................................... ; ........................................ .

Дисперсія та с.к.п. функції

....................................................................................................................

................................................................... ................................................ .

б) Визначення с.к.похибок аргументів коли с.к. похибка = ..................... (табл.6, графа 5).

Приймаємо ........................................................................................................................................

..............................................................................................................................................................

Тоді ............................................; а ............................... .

С.к.похибки аргументів

.......................................... ; = ............................................ .

7. Функція

а) Визначаємо похідні

= ...................... = ....................... ; = ....................... = ................... .

Дисперсія та с.к. похибка функції

= ................................................................................................................................

............................................................................. = .................................................. .

б) Визначення с.к.похибок аргументів, коли = .......... мм (табл.6, графа 5).

Приймаємо ...............................................................................................................................

...................................................................................................................................................

Тоді = .................................................., а .................................... .

С.к. похибки аргументів

= ....................................... ; = ................................. .

8. Функція

а) Визначаємо похідні

= ...................................... = ..........; = ................................... = ............... .

Дисперсія та с.к. похибка функції

= ................................................................................................................................

................................................................................. ........................................... .

б) Визначення с.к. похибок аргументів, коли = ......... мм (табл. 6, графа 5).

Приймаємо ....................................................................................................................................

..........................................................................................................................................................

Тоді = ............................................. , а ........................ .

С.к. похибки аргументів

= ............................................. ; = ...................................... .