Визначення кореляційної матриці

Завдання 7. (Приклад 16). На пункті тріангуляції способом кругових прийомів виміряні кути та (рис.1).Середня “0” лімба квадратична похибка вимірювання напряму дорівнює . Визначити кореляційну матрицю , коефіцієнти кореляції між виміряними кутами та дисперсію кута

Вихідні дані: .

.

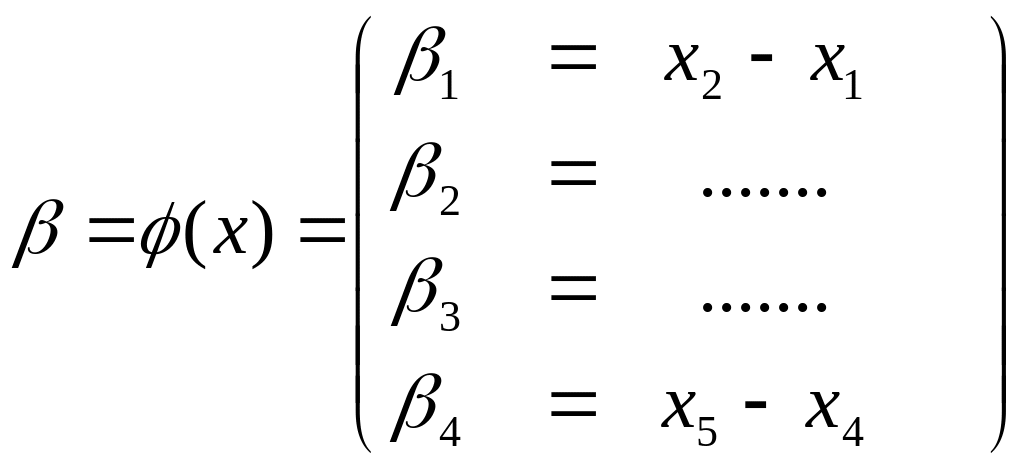Визначимо коефіцієнти кореляційної матриці А

; ; ;

= ................; = ................ ; = .............. ;

= ................. ; = ................. ; = ............. ;

= ................ ; = .................. ; = ................ ;

;

= ................; = ................ ;

= ................. ; = ..................;

= ................ ; = .................. ;

Кореляційна матриця буде

= .

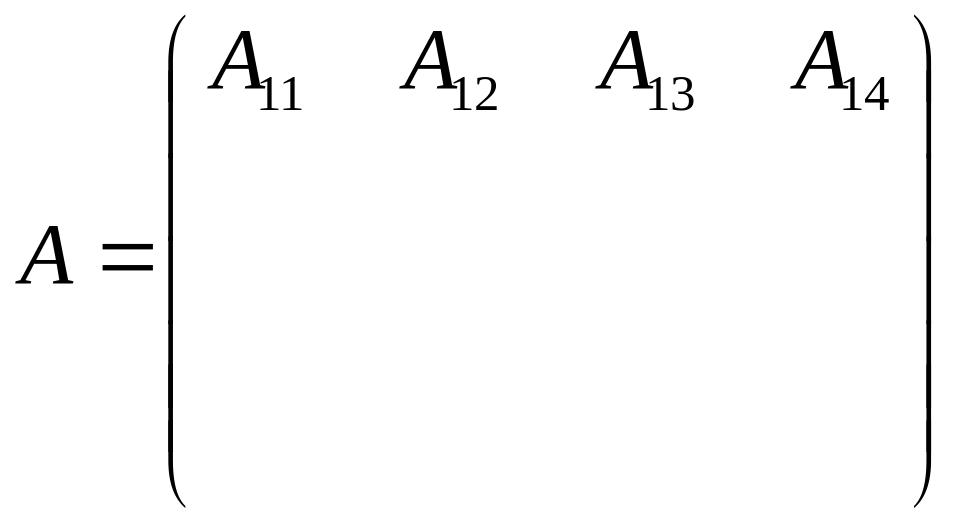Оскільки вимірювання кутів рівноточні, то кореляційна матриця = .......... ,

де E - одинична матриця

Кореляційна матриця функції виміряних кутів на пункті тріангуляції визначиться:

A

= ;

або = .

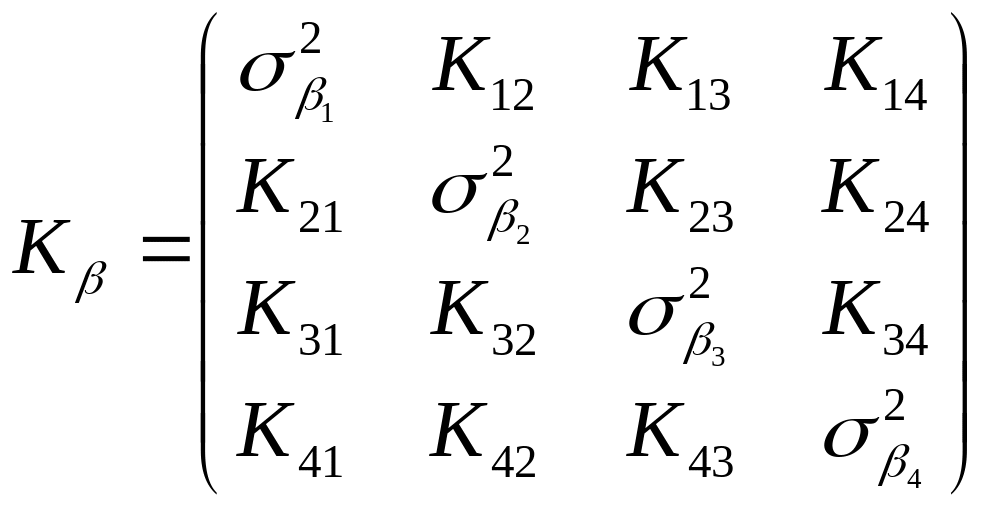Коефіцієнти кореляції між виміряними кутами

............. ; ............. ; ............ .

............. ; ............... ; .................... .

............. ; ............... ; .............. .

.............. ; ............... ; .................. .

Нормована кореляційна матриця

.

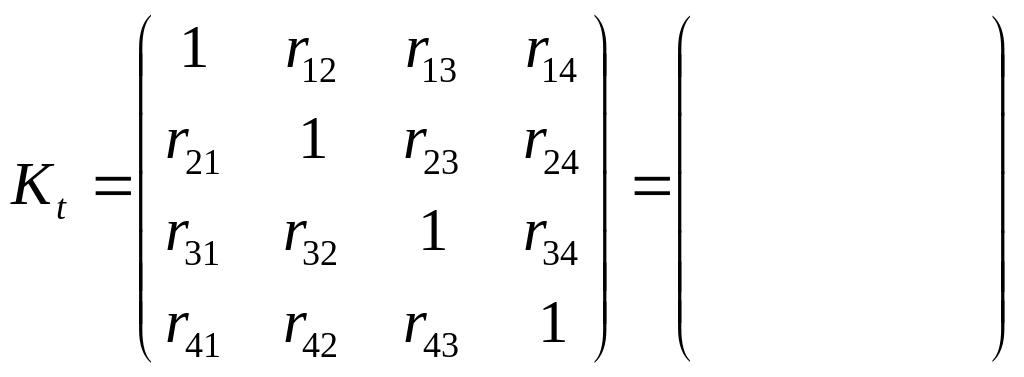Дисперсія кута дорівнює:

Обробка статистичного ряду вимірів

Завдання 8. (Приклад 17). При експериментальних дослідженнях горизонтальний кут виміряно 60 прийомами. Необхідно: 1) побудувати ступінчатий графік, гістограму та полігон частот; 2) обчислити асиметрію та ексцес статистичного ряду. Результати вимірів та необхідні обчислення подаються в таблиці 1.

Таблиця 1

№ п\п	Кут ''	’’				за зрос- танням	Інтервал	Частота	Нормовані
1	2	3	4	5	6	7	8	9	10
1	1.1
2
3	3.3
4	4.3
5	5.4
6	1.8
7	2.5
8	3.0
9	3.1
10	3.3
11	4.8
12	5.6
13	6.4
14
15	3.4
16	4.9
17
18	3.8
19	4.0
20	4.1
21	4.7
22	5.0
23	6.1
24	5.5
25	5.0
26	3.9
27	5.1
28	3.7
29	4.7
30	3.6
31
32	4.2
33	5.6
34	4.0
35	3.2
36	3.8
37	3.9
38	5.8
39	6.4
40
41
42
43	2.9
44	3.3
45	4.6
46	5.0
47	4.4
48	2.5
49	2.8
50	3.7
51	4.1
52	6.0
53	6.2
54	4.8
55	4.3
56	4.2
57	3.0
58	3.4
59	4.7
60	4.5