Занятие № 1

Радианная мера углов. Тригонометрические функции угла и числового аргумента. Соотношения между тригонометрическими функциями одного аргумента.

1. Понятие угла
В геометрии		В тригонометрии
У гол - геометрическая фигура, об­разованная двумя лучами, которые выходят из одной точки. АОВ образован лучами ОА и ОВ		Угол — фигура, образованная при повороте луча на плоскости около начальной точки. АОВ образован при повороте луча ОА около точки О
2. Измерение углов
Градусная мера угла (10 = часть развернутого угла)
Каждому углу ставится в соответ­ствие градусная мера [0°; 180°]. АОВ = 900		Каждому углу как фигуре ставится в соответствие угол поворота, с по­мощью которого образован этот угол. Угол поворота (- ; + ). АОВ = = 900 АОВ = = - 2700 АОВ = = = 900 + 3600 = 4500
Радианная мера угла
	1 радиан — центральный угол, соответствующий дуге, длина которой равна радиусу окружности. АОВ = 1 рад. Это означает, что АВ = ОА = R АОС = 1800 = (радиан) АОС – развернутый. 10 = радиан 1 радиан = 570

Примеры.

1. Выразите в радианах величины углов:30⁰; 45⁰; 60⁰; 90⁰; 270⁰; 360⁰.

Решение: Поскольку 30⁰ – это часть угла 180⁰, то из равенства 180⁰ = (рад) получаем, что 30⁰ = (рад).

В общем случае учитываем, что 1⁰ = радиан, тогда:

45⁰ = 45 = (рад);

60⁰ = 60 = (рад);

90⁰ = 90 = (рад);

270⁰ = 270 = (рад);

360⁰ = 360 = (рад);

2. Выразите в градусах величины углов: ; ; ; 5.

Решение: Поскольку - это часть угла , то из равенства =180⁰ получаем, что = 18⁰.

В общем случае учитываем, что 1 радиан = , тогда:

= = 120⁰;

= = 135⁰;

3. Изобразите угол, образованный поворотом луча ОА около точки О на:

1. 270⁰;

2. -270⁰;

3. 720⁰;

4. -90⁰;

5. 225⁰;

6. -45⁰;

7. 540⁰;

8. -180⁰;

9. 360⁰;

10. -60⁰.

4. Чему равны углы поворота, показанные на рисунке

1) 2) 3) 4)

5. Выразите в радианной мере величины углов:

1. 225⁰;

2. 36⁰;

3. 100⁰;

4. -240⁰;

5. -22,5⁰;

6. -150⁰.

6. Выразите в градусной мере величины углов:

1. 3 ;

2. ;

3. - ;

4. ;

5. - ;

6. ;

7. - ;

8. 3.

3. Определение тригонометрических функций
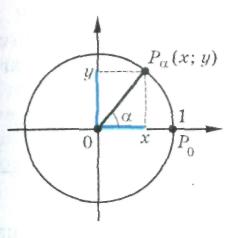
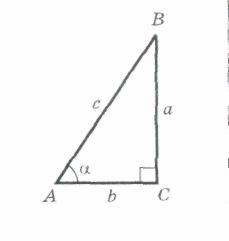
Через единичную окружность (R = 1)	Через произвольную окружность (R – радиус окружности)		Через прямоугольный треугольник (для острых углов)
sin = у – ордината точки Р cos = х – абсцисса точки Р tg = = сtg = =	sin = cos = tg = сtg =		sin = cos = tg = сtg =
4. Тригонометрические функции числового аргумента
sin(числа ) = sin(угла в радиан) cos (числа ) = cos (угла в радиан) tg (числа ) = tg (угла в радиан) сtg (числа ) = сtg (угла в радиан)
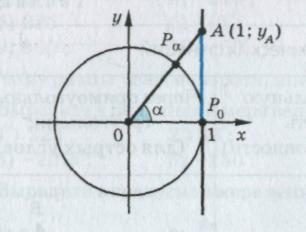
5. Линии тангенсов и котангенсов
АР0 – линия тангенсов (АР0 Оу) tg = уА - ордината соответствующей точки линии тангенсов		СВ – линия котангенсов (СВ Ох ) сtg = хВ – абсцисса соответствующей точки линии котангенсов

6. Знаки тригонометрических функций
7. Четность и нечетность
Косинус — четная функция cos (- ) = cos	Синус, тангенс и котангенс —нечетные функции sin (- ) = - sin tg (- ) = - tg сtg (- ) = - сtg
8. Функция f(х) называется периодической с периодом Т 0, если для любых х из области определения функции числа (х + Т) и (х - Т) также принадлежат области определения и выполняется равенство f (х + Т) = f (х - Т) = f (х).
у = - дробная часть числа х	Через промежутки длиной Т (на оси Ох) вид графика периодической функции повторяется
	Если Т – период функции, то Т, 2Т, 3Т, …, kТ – также периоды этой функции (k N)
sin (x+ 2 ) = sin x cos (x + 2 ) = cos x	Функции sin х и cos х имеют период Т = 2	Т = 2 - общий период для всех функций: sin х, cos х, tg х, ctg х
tg (x + ) = tg x ctg (x + ) = ctg x	Функции tg х и ctg х имеют период Т =

	градусы	0°	30°	45°	60°	90°	180°	270°	360°
	радианы	0							2
sin		0				1	0	- 1	0
cos		1				0	- 1	0	1
tg		0		1		-	0	-	0
сtg		—		1		0	-	0	-

Примеры:

1. Пользуясь периодичностью, четностью и нечетностью тригонометрических функций, найдите:

1. sin ;

2. sin (- 750⁰);

3. sin ;

4. cos (- 405⁰);

5. cos ;

6. tg ;

7. tg 600⁰;

8. tg ;

9. ctg (- 570⁰);

10. ctg 945⁰;

11. ctg .

Примеры решения задач: 1) sin = sin = sin = sin = sin = sin = 1 (Учитывая, что значение функции sin х повторяется через период 2 , выделим в заданном аргументе число, кратное периоду (то есть 10 ), а потом воспользуемся равенством

sin (2 + ) = sin .);

2) cos (- 750⁰) = cos (2·360⁰ + 30⁰) = cos 30⁰ = . (Сначала учитываем четность косинуса:

cos (- ) = cos , а потом его периодичность с периодом 2 = 360⁰: cos ( +360⁰) = cos .)

2. Найдите период каждой из данных функций:

1. у = cos 2x;

2. у = tg 5x;

3. у = cos ;

4. у = sin ;

5. у = ctg 3x;

6. у = cos .

Примеры решения задач: Если функция у = f(х) периодическая с периодом Т, то функция

у = Аf (kx + b) также периодическая с периодом Т₁ = (А, k, b – некоторые числа и k 0).

1) у = sin 4х: А = 1, k = 4, b = 0, период функции у = sin х равен Т = 2 , следовательно,

Т₁ = = ;

2) у = tg : А = 1, k = , b = 0, период функции у = tg х равен Т = , следовательно,

Т₁ = = = 4 .

3. Вычислить:

1. 3cos - sin + ctg ;

2. 2 sin - tg + cos ;

3. 2 sin - cos + tg ;

4. tg - sin + cos ;

5. 2 cos 60⁰ + cos 30⁰;

6. 5 sin 30⁰ - ctg 45⁰;

7. 2 sin 30⁰ + 6 cos 60⁰ – 4 tg 45⁰;

8. 3 tg 45⁰ sin 60⁰;

9. 4 tg 60⁰ tg 60⁰;

10. 12 sin 60⁰ cos 60⁰;

11. 2 sin 60⁰ ctg 60⁰;

12. 2 sin 45⁰ - cos 30⁰;

13. 7 tg 30⁰ сtg 30⁰;

14. 6 сtg 60⁰ - 2 sin 60⁰.

Примеры решения задач:

2 sin - cos + tg = 2 0 - 0 + = .

4. Привести к одноименной функции острого угла:

1. cos 1827^0;

2. tg 978^0;

3. sin (-800⁰);

4. ctg 1305^0;

5. sin ;

6. tg ;

7. ctg .

Примеры решения задач:

sin 1782⁰ = sin(5 · 360⁰ - 18⁰) = sin(- 18⁰) = - sin18⁰

5. Вычислить значение тригонометрической функции:

1. cos 1125^0;

2. cos (-315⁰);

3. tg ;

4. cos

5. sin 390⁰;

6. cos 420⁰;

7. tg 540^0;

8. ctg 450^0;

9. sin 405⁰;

10. cos 720⁰;

11. tg 390^0;

12. сtg 630^0;

13. sin (-720⁰);

14. cos (-405⁰);

15. cos (-780⁰);

16. ctg (-1110⁰);

17. tg (-900⁰);

18. ctg (-780⁰);

19. sin (-1125⁰).

9. Соотношения между тригонометрическими функциями одного аргумента
cos = х sin = у	Основное тригонометрическое тождество
	tg = ctg = tg · ctg = 1 1 + tg2 = 1 + ctg2 =

Примеры решения задач:

1. Зная значение одной из тригонометрических функций и интервал, в котором находится , найдите значение трех остальных тригонометрических функций:

sin = , 90⁰ < < 180⁰.

Решение:

1) Равенство связывает cos и sin и позволяет выразить одну из этих функций через другую. Например, .Тогда . Учитывая, в какой четверти находится , мы можем определить знак, который необходимо взять в правой части формулы (это знак косинуса во ІІ четверти). Зная, cos и sin , находим tg = и ctg = . Укажем, что после нахождения tg значение сtg можно также найти из соотношения tg · ctg = 1.

Итак, из равенства получаем: . Отсюда . Поскольку 90⁰ < < 180⁰, то , а значит, . Тогда tg = = , ctg = = .

2. Упростите выражение .

Примеры решения задач:

Для преобразования числителя данной дроби из основного тригонометрического тождества находим: . Затем, используя определение тангенса:

tg = , упрощаем полученную дробь. Итак, = .