Контрольная работа по дисциплине «Статистические методы анализа социально-экономических явлений» для студентов группы умз-14-1 Краткая теоретическая справка

Будем понимать под явлением – совокупность условий и катализируемых ими значимых социально-экономических событий и процессов. Социально-экономические процессы и явления чаще всего имеют стохастическую природу и представляются случайными скалярными и векторными величинами. Целями анализа является извлечение закономерной информации о социально-экономических явлениях и эволюции социально-экономических процессов из массивов наблюденных значений случайных величин, характеризующих процессы.

Для этого используются инструменты, разработанные в теории вероятностей и математической статистике.

1. Распределение и плотность вероятностей

Пусть имеется величина Х, принимающая случайным образом некоторые вещественные значения. Задан ряд значений этой величины: х₁, х₂, х₃,... х_n . Упорядоченное наглядное представление случайной величины Х дается функцией распределения (Рис.1) и плотностью распределения (Рис.2) вероятностей Х.

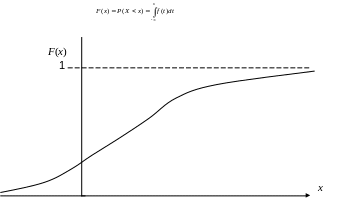
Рис.1. Функция распределения случайной величины Х

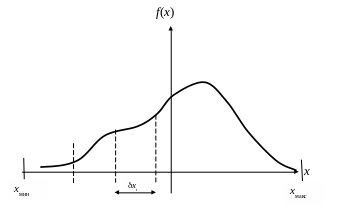
Рис.2. Плотность вероятностей случайной величины Х

2. Гистограмма

На практике для визуального представления часто используется эмпирическая плотность распределения, которая называется гистограммой. Технология её построения достаточно проста. Диапазон значений Х (размах), на рис.2 х= х_макс-х_мин , разбивается на некоторое число карманов х_i . Количество и величина карманов выбираются в зависимости от требуемой детализации распределения и затрат времени на построение: чем больше карманов, тем точнее представление, но больше объем вычислений.

Далее из множества значений х₁, х₂, х₃,... х_n выбираются принадлежащие первому х₁ карману. Пусть их число n₁, n₂, ..., n_k, где k – количество карманов.

Определяются относительные частоты

(1)

и строится графическое представление, показанное на рис.3 и называемое гистограммой.

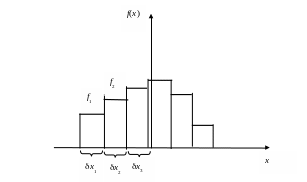
Рис.3. Гистограмма

3. Параметры распределения

Для характеризации случайной величины используются параметры распределения: среднее значение и дисперсия или квадратный корень из неё - среднее квадратическое отклонение. Они вычисляются по массиву имеющихся значений случайной величины х₁, х₂, х₃,... х_n следующим образом. Среднее значение х₁, х₂, х₃,... х_n равно:

(2)

где  - обозначает математическое ожидание (среднее значение), Е – обозначает операцию взятия математического ожидания (нахождения среднего) , i=1,2, ..., n – значения случайной величины Х, f_i­ – вероятности .

При использовании гистограммы в (2), вместо подставляются средние значения интервалов х_i, и вероятностями выступают относительные частоты (1).

Если значения равновероятны и их вероятности f_i­= 1/n, то (2) принимает вид:

(3)

Дисперсия и среднеквадратическое отклонение (СКО) по массиву имеющихся значений случайной величины х₁, х₂, х₃,... х_n определяются следующим образом:

. (4)

Средне квадратическое отклонение (СКО) равно корню квадратному из дисперсии, т.е. .

Для n измеренных равновероятных значений (4) приобретает вид:

. (5)

По ограниченным наборам измеренных значений случайной величины обычно определяют не дисперсию случайной величины, а её оценку. Для получения несмещенной оценки дисперсии в (5) используется деление не на n, а на n-1, т.е.

. (5а)

Это существенно при малых значениях n и такие тонкости следует учитывать при решении научных задач.