Вариант №1

1. Что называется допустимым решением задачи линейного программирования? Что называется оптимальным решением задачи линейного программирования?

2. Какая игра называется матричной? Что называется матрицей игры?

3. Что такое производственная функция?

4. Найдите максимальное значение целевой функции при ограничениях

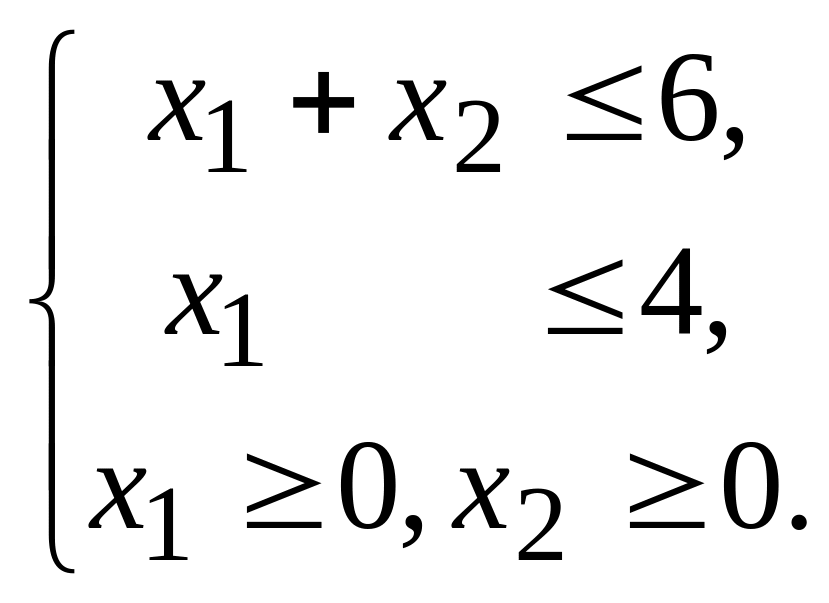и запишите для неё двойственную задачу.

5. Найдите значения параметра а, при котором транспортная задача

	тарифы			запасы
	1		2
1	4	0		50
2	2	5		60+2а
3	3	8		150
потребности	100+а	200

будет закрытой.

6. Фирма может выставить на рынок 4 вида товаров. Рынок может находиться в 5 состояниях, в зависимости от которых доходы фирмы в денежных единицах представлены матрицей .

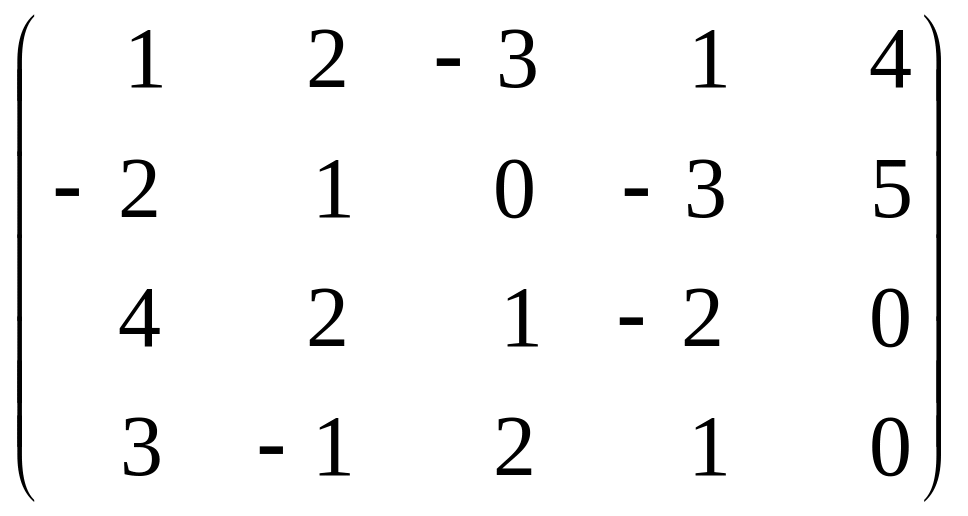Требуется составить модель матричной игры и найти

а) нижнюю цену игры и все максиминные стратегии игрока 1;

б) верхнюю цену игры и все минимаксные стратегии игрока 2;

в) цену игры и седловые точки, если они существуют;

7. Дана функция полезности . Найти уравнения кривых безразличия.

Вариант №2

1. Что называется канонической формой задачи линейного программирования?

2. Что называется нижней ценой игры и максиминной стратегией игрока 1? Сформулируйте правило нахождения нижней цены игры и максиминной стратегии.

3. Какой вид имеет функция Кобба-Дугласа?

4. Найдите максимальное значение целевой функции при ограничениях

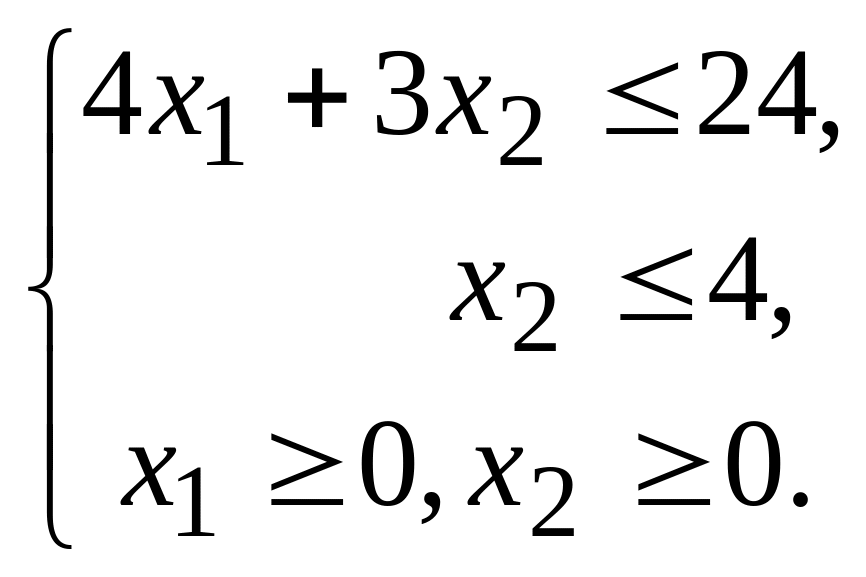и запишите для неё двойственную задачу.

5. Найдите значения параметра а, при котором транспортная задача

	тарифы			запасы
	1		2
1	2	1		50
2	4	5		60+3а
3	3	8		50
потребности	100+а	100

будет закрытой.

6. Фирма может выставить на рынок 4 вида товара. Рынок может находиться в 5 состояниях, в зависимости от которых доходы фирмы в денежных единицах представлены матрицей .

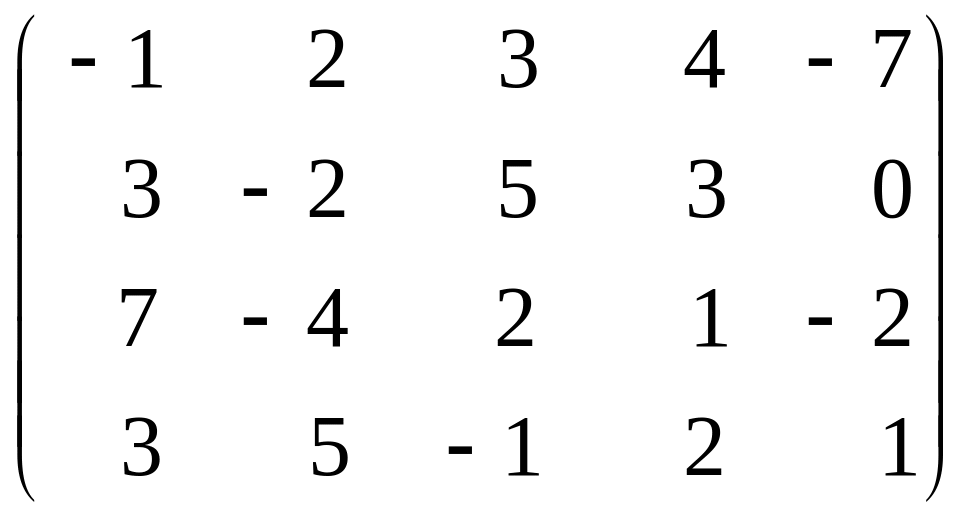Требуется составить модель матричной игры и найти

а) нижнюю цену игры и все максиминные стратегии игрока 1;

б) верхнюю цену игры и все минимаксные стратегии игрока 2;

в) цену игры и седловые точки, если они существуют;