- •Оглавнение
- •Тема 1. Развитие понятия о числе
- •Тема 2. Корни, степени, логарифмы.
- •Примерная структура заданий для самостоятельной работы
- •Содержание дисциплины «Математика»
- •Тема 1. Развитие понятия о числе.
- •Тема 2. Корни, степени, логарифмы.
- •Самостоятельная работа №1.
- •Теоретический материал.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Самостоятельная работа №2.
- •Теоретический материал.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Самостоятельная работа №3.
- •Теоретический материал.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Тема 2. Корни, степени, логарифмы. Самостоятельная работа №4.
- •Теоретический материал.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Самостоятельная работа №5.
- •Теоретический материал.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Самостоятельная работа №6.
- •Теоретический материал.
- •Основное логарифмическое тождество
- •Логарифмическая функция при основании, меньшем 1
- •Десятичные и натуральные логарифмы
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Самостоятельная работа №7.
- •Теоретический материал.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Самостоятельная работа №8.
- •Теоретический материал.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Тема 3. Прямые и плоскости в пространстве. Самостоятельная работа №9.
- •Теоретический материал.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Самостоятельная работа №10.
- •Теоретический материал.
- •Основные источники:
- •Дополнительные источники:
- •Тема 4. Элементы комбинаторики.
- •Теоретический блок.
- •Блок практических заданий (выполнение заданий по алгоритму, типовые расчеты, ответы на контрольные вопросы, …).
- •Графическая часть.
- •Блок повышенного уровня (сравнить, составить алгоритм, сделать теоретический вывод, …).
- •Рекомендуемая литература. Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Тема 5. Координаты и векторы. Самостоятельная работа №12.
- •Теоретический материал.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Самостоятельная работа №13.
- •Теоретический материал.
- •Основные источники:
- •Дополнительные источники:
- •Тема 6. Основы тригонометрии.
- •Преобразование суммы (разности) тригонометрических функций в произведение (преобразование тригонометрических выражений к виду, удобному для логарифмирования).
- •Преобразование произведения тригонометрических функций в сумму.
- •Простейшие соотношения между обратными тригонометрическими функциями.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Самостоятельная работа №15.
- •Теоретический материал.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Самостоятельная работа №16.
- •Теоретический материал.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Самостоятельная работа №17.
- •Теоретический материал.
- •1.Выбор и обснование основных параметров двигателя
- •Оценка, расчет и выбор конструктивных параметров двигателя
- •1. Оценка и выбор параметров двигателя
- •1.1 Число и расположение цилиндров
- •1.2 Средняя скорость поршня и частота вращения
- •1.3 Диаметр цилиндра и ход поршня
- •1.4 Длина шатуна
- •1.5 Степень сжатия
- •1.6 Фазы газораспределения
- •2. Описание конструкции и систем двигателя
- •2.1 Блок-картер
- •2.2 Головка цилиндров
- •2.3 Гильзы цилиндров
- •2.4 Механизм газораспределения
- •2.9 Система питания
- •3.1.2 Упрощённый расчёт наполнения
- •3.1.3 Определение параметров рабочего тела в конце процесса сжатия
- •3.1.4 Определение параметров рабочего телав конце "видимого" горения
- •3.1.5Определение параметров рабочего тела в конце процесса расширения
- •3.1.6 Индикаторные показатели двигателя
- •3.1.7 Эффективные показатели двигателя
- •3.1.8 Показатели турбины и нагнетателя
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Тема 7. Функции и их свойства и графики. Самостоятельная работа №18.
- •Теоретический материал.
- •1. Общие свойства функций.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Тема 8. Многогранники. Самостоятельная работа №19.
- •Теоретический материал.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Тема 9. Тела и поверхности вращения. Самостоятельная работа №20.
- •Теоретический материал.
- •Вариант №1
- •Вариант №1
- •Вариант №2
- •Основные источники:
- •Дополнительные источники:
- •Тема 10. Начала математического анализа.
- •Свойства числовых последовательностей.
- •Арифметическая прогрессия.
- •Геометрическая прогрессия.
- •Предел последовательности.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Самостоятельная работа №22.
- •Теоретический материал.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Самостоятельная работа №23.
- •Теоретический материал. Интегралы.
- •Неопределённый интеграл и его свойства.
- •Простейшие правила интегрирования.
- •Определенный интеграл.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Тема 11. Измерения в геометрии. Самостоятельная работа №24.
- •Теоретический материал.
- •Вариант 1
- •Вариант 2
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Тема 12. Элементы теории вероятностей. Элементы математической статистики. Самостоятельная работа №25.
- •Теоретический материал.
- •Математическая статистика.
- •Математическая статистика.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Самостоятельная работа №26.
- •Теоретический материал.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Тема 13. Уравнения и неравенства. Самостоятельная работа №27.
- •Теоретический материал.
- •Квадратные уравнения и неравенства.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Тема 14. Предэкзаменационное повторение. Самостоятельная работа №28.
- •Теоретический материал.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
Основные источники:
Башмаков М.И., математика: учебник для нач. и сред. Проф. образования, -М.: Образовательно-издательский центр «Академия», 2010.- 256 с.
Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 10 кл. – М., 2005.
Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 11 кл. – М., 2005.
Башмаков М.И. Математика (базовый уровень). 10—11 кл. – М., 2005.
Башмаков М.И. Математика: 10 кл. Сборник задач: учеб. пособие. – М., 2004.
Дополнительные источники:
Алимов Ш.А. и др. Алгебра и начала анализа. 10 (11) кл. – М., 2000.
Атанасян Л.С. и др. Геометрия. 10 (11) кл. – М., 2000.
Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 10 кл. – М., 2005.
Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 11 кл. – М., 2005.
Башмаков М.И. Математика (базовый уровень). 10—11 кл. – М., 2005.
Башмаков М.И. Математика: 10 кл. Сборник задач: учеб. пособие. – М., 2004.
Башмаков М.И. Математика: учебник для 10 кл. – М., 2004.
Колмогоров А.Н. и др. Алгебра и начала анализа. 10 (11) кл. – М., 2000.
Колягин Ю.М. и др. Математика (Книга 1). – М., 2003.
Колягин Ю.М. и др. Математика (Книга 2). – М., 2003.
Луканкин Г.Л., Луканкин А.Г. Математика. Ч. 1: учебное пособие для учреждений начального профессионального образования. – М., 2004.
Пехлецкий И.Д. Математика: учебник. – М., 2003.
Смирнова И.М. Геометрия. 10 (11) кл. – М., 2000.
Интернет ресурсы:
Колмогоров А.Н. (ред.) — Алгебра и начала анализа: Электронная книга.Lib.mexmat.ru/books/3307
Алгебра и начала анализа. 10-11 класс. Учебник. Мордкович
e-ypok.ru/content/
Математика для колледжей » Математический Портал – библиотека math-portal.ru
Тема 11. Измерения в геометрии. Самостоятельная работа №24.
Тема: Измерения в геометрии (решение задач).
Время выполнения задания – 6ч.
Цель работы: Закрепление знаний и умений по измерениям в геометрии.
Теоретический материал.
Вычисление площади.
При
измерении площади фигуры
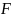 получается число
получается число
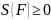 .
За единицу площади (масштаба) принимается
квадрат со стороной, равной единице
длины.
.
За единицу площади (масштаба) принимается
квадрат со стороной, равной единице
длины.
Для вычисления площади различных геометрических фигур применяются формулы, которые указаны в таблице:
№ п/п |
Фигура |
Формула |
Описание формулы |
1 |
Прямоугольник |
|
|
2 |
Параллелограм |
|
– стороны
параллелог-рамма,
|
3 |
Прямоугольный треугольник |
|
- катеты |
4 |
Равнобедренный треугольник |
|
– основание, - бедро, - высота, – уголь у основания треугольника
|
5 |
Правильный треугольник |
|
– сторона треуголь-ника, - радиус, описанного круга |
6 |
Произвольный треугольник |
|
– основание, - бедро, - высота, – уголь у основания треугольника |
7 |
Трапеция |
|
– основания, - высота трапеции |
8 |
Круг |
|
– радиус
круга, а
|
9 |
Круговой сектор |
|
– радиус,
|
Вычисление объема.
Для вычисления объема различных геометрических фигур применяются формулы, которые указаны в таблице:
№ п/п |
Фигура |
Формула |
Описание формулы |
1 |
Куб |
|
|
2 |
Прямая призма |
|
-
высота,
|
3 |
Прямой цилиндр |
|
- высота, - площадь основания цилиндра |
4 |
Пирамида |
|
- высота, - площадь основания пирамиды |
5 |
Конус |
|
- высота, - площадь основания конуса |
6 |
Шар |
|
– радиусшара |
Решение примеров и задач (алгоритм выполнения задания):
Пример
1.
Чему равна площадь прямоугольника с
длиной
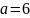 см и шириной
см и шириной
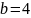 см?
см?
Решение. Площадь прямоугольника можно вычислить по формуле (из таблицы):
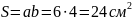 .
.
Пример
2.
Вычислите площадь параллелограмма с
сторонами
 см и шириной
см и шириной
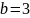 см и углом между ними
см и углом между ними
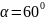 .
.
Решение. Площадь параллелограмма можно вычислить по формуле(из таблицы) :
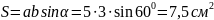 .
.
Пример
3.
Чему равна площадь прямоугольного
треугольника с катетом
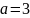 см и гипотенузой
см и гипотенузой
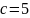 см?
см?
Решение. Площадь прямоугольного треугольника можно вычислить по формуле (из таблицы):
.
можно
вычислить из формулы:
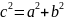 ,
,
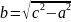 =
=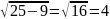 см.
см.
Тогда
 .
.
Пример
4.
Чему равна площадь равнобедренного
треугольника с основанием
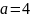 см и бедром
см и бедром
 см?
см?
Решение. Площадь равнобедренного треугольника можно вычислить по формуле (из таблицы):
 ,
,
где
 =
=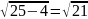 см.
см.
Тогда
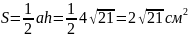 .
.
Пример
5.
Чему равна площадь Трапеции с основаниями
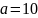 см,
см и бедром
см?
см,
см и бедром
см?
Решение. Площадь Трапеции можно вычислить по формуле (из таблицы):
,
где
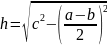 =
см.
=
см.
Тогда
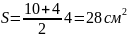 .
.
Пример
6.
Вычислите площадь круга с радиусом
 см.
см.
Решение. Площадь круга можно вычислить по формуле (из таблицы) :
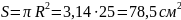 .
.
Пример
7.
Вычислите объем куба с сторонами
м,
м и
 м.
м.
Решение. Объем куба можно вычислить по формуле (из таблицы) :
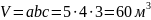 .
.
Пример
8.
Вычислите объем прямого цилиндра с
высотой
см и радиусом
 cм.
cм.
Решение. Объем прямого цилиндра можно вычислить по формуле (из таблицы) :
 .
.
Пример
9.
Вычислите объем конуса с высотой
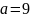 см и радиусом
см и радиусом
 cм.
cм.
Решение. Объем конуса можно вычислить по формуле(из таблицы) :
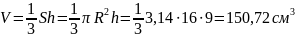 .
.
Пример
10.
Вычислите объем шара радиусом
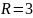 м.
м.
Решение. Объем шара можно вычислить по формуле (из таблицы) :
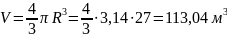 .
.
Решите примеры:

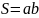
 – стороны
прямоугольника
– стороны
прямоугольника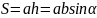
 - высота,
- высота,
 - уголь между сторонами (
- уголь между сторонами (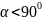 )
)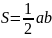
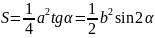
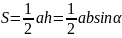
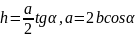
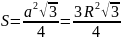
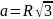

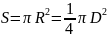
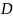 - диаметр,
- диаметр,
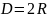 .
.
 - длина круга сектора,
– уголь
- длина круга сектора,
– уголь
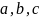 – стороны
куба
– стороны
куба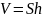
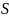 - площадь основания призмы
- площадь основания призмы