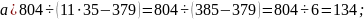- •Оглавнение
- •Тема 1. Развитие понятия о числе
- •Тема 2. Корни, степени, логарифмы.
- •Примерная структура заданий для самостоятельной работы
- •Содержание дисциплины «Математика»
- •Тема 1. Развитие понятия о числе.
- •Тема 2. Корни, степени, логарифмы.
- •Самостоятельная работа №1.
- •Теоретический материал.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Самостоятельная работа №2.
- •Теоретический материал.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Самостоятельная работа №3.
- •Теоретический материал.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Тема 2. Корни, степени, логарифмы. Самостоятельная работа №4.
- •Теоретический материал.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Самостоятельная работа №5.
- •Теоретический материал.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Самостоятельная работа №6.
- •Теоретический материал.
- •Основное логарифмическое тождество
- •Логарифмическая функция при основании, меньшем 1
- •Десятичные и натуральные логарифмы
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Самостоятельная работа №7.
- •Теоретический материал.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Самостоятельная работа №8.
- •Теоретический материал.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Тема 3. Прямые и плоскости в пространстве. Самостоятельная работа №9.
- •Теоретический материал.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Самостоятельная работа №10.
- •Теоретический материал.
- •Основные источники:
- •Дополнительные источники:
- •Тема 4. Элементы комбинаторики.
- •Теоретический блок.
- •Блок практических заданий (выполнение заданий по алгоритму, типовые расчеты, ответы на контрольные вопросы, …).
- •Графическая часть.
- •Блок повышенного уровня (сравнить, составить алгоритм, сделать теоретический вывод, …).
- •Рекомендуемая литература. Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Тема 5. Координаты и векторы. Самостоятельная работа №12.
- •Теоретический материал.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Самостоятельная работа №13.
- •Теоретический материал.
- •Основные источники:
- •Дополнительные источники:
- •Тема 6. Основы тригонометрии.
- •Преобразование суммы (разности) тригонометрических функций в произведение (преобразование тригонометрических выражений к виду, удобному для логарифмирования).
- •Преобразование произведения тригонометрических функций в сумму.
- •Простейшие соотношения между обратными тригонометрическими функциями.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Самостоятельная работа №15.
- •Теоретический материал.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Самостоятельная работа №16.
- •Теоретический материал.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Самостоятельная работа №17.
- •Теоретический материал.
- •1.Выбор и обснование основных параметров двигателя
- •Оценка, расчет и выбор конструктивных параметров двигателя
- •1. Оценка и выбор параметров двигателя
- •1.1 Число и расположение цилиндров
- •1.2 Средняя скорость поршня и частота вращения
- •1.3 Диаметр цилиндра и ход поршня
- •1.4 Длина шатуна
- •1.5 Степень сжатия
- •1.6 Фазы газораспределения
- •2. Описание конструкции и систем двигателя
- •2.1 Блок-картер
- •2.2 Головка цилиндров
- •2.3 Гильзы цилиндров
- •2.4 Механизм газораспределения
- •2.9 Система питания
- •3.1.2 Упрощённый расчёт наполнения
- •3.1.3 Определение параметров рабочего тела в конце процесса сжатия
- •3.1.4 Определение параметров рабочего телав конце "видимого" горения
- •3.1.5Определение параметров рабочего тела в конце процесса расширения
- •3.1.6 Индикаторные показатели двигателя
- •3.1.7 Эффективные показатели двигателя
- •3.1.8 Показатели турбины и нагнетателя
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Тема 7. Функции и их свойства и графики. Самостоятельная работа №18.
- •Теоретический материал.
- •1. Общие свойства функций.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Тема 8. Многогранники. Самостоятельная работа №19.
- •Теоретический материал.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Тема 9. Тела и поверхности вращения. Самостоятельная работа №20.
- •Теоретический материал.
- •Вариант №1
- •Вариант №1
- •Вариант №2
- •Основные источники:
- •Дополнительные источники:
- •Тема 10. Начала математического анализа.
- •Свойства числовых последовательностей.
- •Арифметическая прогрессия.
- •Геометрическая прогрессия.
- •Предел последовательности.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Самостоятельная работа №22.
- •Теоретический материал.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Самостоятельная работа №23.
- •Теоретический материал. Интегралы.
- •Неопределённый интеграл и его свойства.
- •Простейшие правила интегрирования.
- •Определенный интеграл.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Тема 11. Измерения в геометрии. Самостоятельная работа №24.
- •Теоретический материал.
- •Вариант 1
- •Вариант 2
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Тема 12. Элементы теории вероятностей. Элементы математической статистики. Самостоятельная работа №25.
- •Теоретический материал.
- •Математическая статистика.
- •Математическая статистика.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Самостоятельная работа №26.
- •Теоретический материал.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Тема 13. Уравнения и неравенства. Самостоятельная работа №27.
- •Теоретический материал.
- •Квадратные уравнения и неравенства.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
- •Тема 14. Предэкзаменационное повторение. Самостоятельная работа №28.
- •Теоретический материал.
- •Основные источники:
- •Дополнительные источники:
- •Интернет ресурсы:
Самостоятельная работа №1.
Тема: Развитие понятия о числе (решение примеров).
Время выполнения задания – 6ч.
Цель работы: Закрепление знаний по развитию понятия о числе с помощью решения примеров.
Теоретический материал.
Натуральные числа (естественные числа) — числа, которые возникают естественным образом при счёте.
Можно привести два подхода к определению натуральных чисел, которые, по сути, мало чем отличаются:
- перечисление (нумерование) предметов (первый, второй, третий, …);
- обозначение количества предметов (нет предметов, один предмет, два предмета, …).
Множество всех натуральных чисел принято обозначать латинской буквой N. Множество натуральных чисел является бесконечным, поскольку для любого натурального числа найдётся натуральное число, которое большее него.
Целые числа (от ср.-лат. cifra от араб. صفر (ṣifr) «пустой, нуль») — множество чисел, получающееся в результате арифметических операций сложения (+) и вычитания (-) натуральных чисел.
Множество всех целых чисел принято обозначать латинской буквой Z.
Результатом сложения, вычитания и умножения двух целых чисел будет только целое число. Целые числа состоят из натуральных чисел (1, 2, 3...), чисел вида «-n» (-1, -2, -3...) и числа нуль.
Необходимость введения целых чисел в математике обусловлена невозможностью (в общем случае) получить разность двух натуральных чисел.
Отрицательные числа ввели в математический обиход Михаэль Штифель (1487—1567) в книге «Полная арифметика» (1544), и Николя Шюке (1445—1500).
Дробные отрицательные числа появляются, например, когда из меньшего дробного числа вычитают большее:
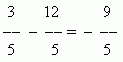
Можно также сказать, что дробные отрицательные числа появляются в результате деления целого отрицательного числа на натуральное:
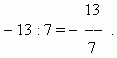
Положительные числа ( целые и дробные ) в противоположность отрицательным числам (целым дробным) рассматриваются в арифметике.
Рациональные числа – это положительные и отрицательные числа (целые и дробные) и ноль. Более точное определение рациональных чисел, принятое в математике, следующее:
Определение: Число называется рациональным, если оно может быть представлено в виде обыкновенной несократимой дроби вида: m / n , где m и n целые числа.
Решение примеров и задач (алгоритм выполнения задания):
1.Выполните действия:
а)
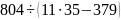 ;
;
б)
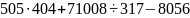 ;
;
в)
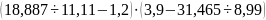 ;
;
г)
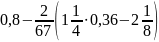 .
.
 Вычислить:
Вычислить:
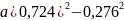 ;
;
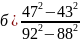 ;
;
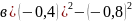 ;
;
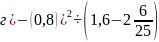 .
.
3. Упростить выражение и найдите его числовое значение
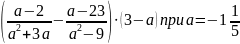 .
.
Решение:
б)
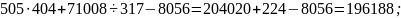
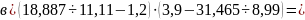
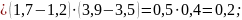
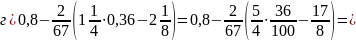
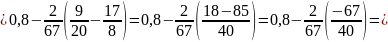
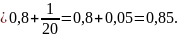

б)
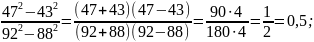
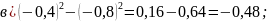
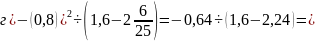
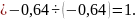
3.
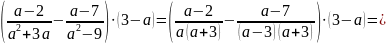
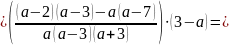

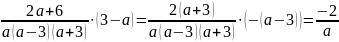
Далее
вставим числовое значение
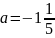 и получим:
и получим:

Решите примеры:
1.Выполните действия:
а)
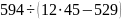 ;
;
б)
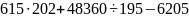 ;
;
в)
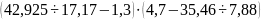 ;
;
г)
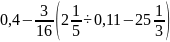 .
.
Вычислить:
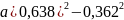 ;
;
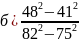 ;
;
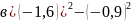 ;
;
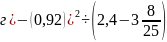 .
.
3. Упростить выражение и найдите его числовое значение
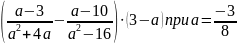 .
.
Вопросы для самоконтроля:
1. Как записывается числа?
2. Что такое натуральные числа?
3. Что такое целые числа?
4. Что такое рациональные числа?
Рекомендуемая литература:
Основные источники:
Башмаков М.И., математика: учебник для нач. и сред. Проф. образования, -М.: Образовательно-издательский центр «Академия», 2010.- 256 с.
Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 10 кл. – М., 2005.
Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 11 кл. – М., 2005.
Башмаков М.И. Математика (базовый уровень). 10—11 кл. – М., 2005.
Башмаков М.И. Математика: 10 кл. Сборник задач: учеб. пособие. – М., 2004.