Основные источники:

1. Башмаков М.И., математика: учебник для нач. и сред. Проф. образования, -М.: Образовательно-издательский центр «Академия», 2010.- 256 с.

2. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 10 кл. – М., 2005.

3. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 11 кл. – М., 2005.

4. Башмаков М.И. Математика (базовый уровень). 10—11 кл. – М., 2005.

5. Башмаков М.И. Математика: 10 кл. Сборник задач: учеб. пособие. – М., 2004.

Дополнительные источники:

1. Алимов Ш.А. и др. Алгебра и начала анализа. 10 (11) кл. – М., 2000.

2. Атанасян Л.С. и др. Геометрия. 10 (11) кл. – М., 2000.

3. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 10 кл. – М., 2005.

4. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 11 кл. – М., 2005.

5. Башмаков М.И. Математика (базовый уровень). 10—11 кл. – М., 2005.

6. Башмаков М.И. Математика: 10 кл. Сборник задач: учеб. пособие. – М., 2004.

7. Башмаков М.И. Математика: учебник для 10 кл. – М., 2004.

8. Колмогоров А.Н. и др. Алгебра и начала анализа. 10 (11) кл. – М., 2000.

9. Колягин Ю.М. и др. Математика (Книга 1). – М., 2003.

10. Колягин Ю.М. и др. Математика (Книга 2). – М., 2003.

11. Луканкин Г.Л., Луканкин А.Г. Математика. Ч. 1: учебное пособие для учреждений начального профессионального образования. – М., 2004.

12. Пехлецкий И.Д. Математика: учебник. – М., 2003.

13. Смирнова И.М. Геометрия. 10 (11) кл. – М., 2000.

Интернет ресурсы:

1. Колмогоров А.Н. (ред.) — Алгебра и начала анализа: Электронная книга.Lib.mexmat.ru/books/3307

2. Алгебра и начала анализа. 10-11 класс. Учебник. Мордкович

e-ypok.ru/content/

3. «Математика для колледжей» Математический Портал – библиотека math-portal.ru

Самостоятельная работа №10.

Тема: Сечение куба плоскостью (построение сечений).

Время выполнения задания – 4ч.

Цель работы: Закрепление знаний и умений по построению сечении куба плоскостью через решения различных задач.

Теоретический материал.

Построение сечений куба. Попробуйте изобразить сечение куба плоскостью в форме четырехугольника.

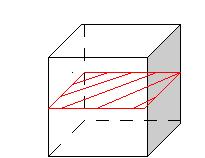
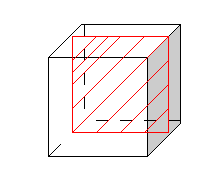
Вопрос: Какая закономерность прослеживается в построении этих сечений?

Ответ: Сечения параллельны граням куба.

Вопрос: Какой четырехугольник получается в сечении в данном случае?

Ответ: квадрат.

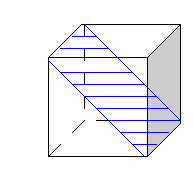
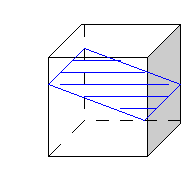
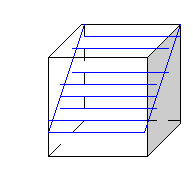
Вопрос: Какая закономерность прослеживается в построении этих сечений?

Ответ: Плоскость сечения параллельна одному из ребер куба или проходит через ребро.

Вопрос: Какой четырехугольник получается в сечении в данном случае?

Ответ: Прямоугольник.

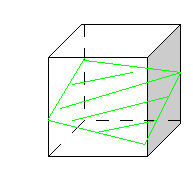
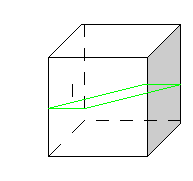
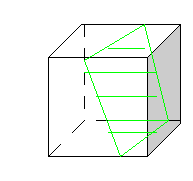Вопрос: Какая закономерность прослеживается в построении этих сечений?

Ответ: Плоскость сечения пересекает четыре параллельных ребра куба .

Вопрос: Какой четырехугольник получается в сечении в данном случае?

Ответ: Параллелограмм.

Рассмотрим теперь вопрос о построении сечений куба.

Решение примеров и задач (алгоритм выполнения задания):

Задача: Пусть дано изображение куба и три точки А, В, С, принадлежащие ребрам этого куба, выходящим из одной вершины.

Решение: Чтобы построить сечение куба плоскостью, проходящей через эти точки, достаточно просто соединить их отрезками. Полученный треугольник АВС и будет искомым изображением сечения куба.

Для построения более сложных сечений используют метод «следов», заключающийся в нахождении точки пересечения прямой и плоскости по заданным двум точкам этой прямой и их проекциям на плоскость. Задача №1.Пусть прямая проходит через точки А, В и известны параллельные проекции А′,В′ этих точек на плоскости π. Требуется найти точку пересечения прямой АВ с плоскостью π.

Решение:Через точки А′,В′ проведем прямую k′. Пересечение прямой k с k′ и будет искомым пересечением прямой k с плоскостью π.

Задача № 2.Даны точки А,В,С и их параллельные проекции А′, В′, С′ на плоскость π.Требуется построить линию пересечения плоскости АВС и плоскости π. Решение:Построить точки Х и У пересечения прямых АВ и АС с плоскостью π.Прямая ХУ будет искомой линией пересечения плоскости АВС и плоскости π.

Задача №3.Через данную точку С (С′) провести прямую, параллельную данной прямой АВ (А′В′), и найти ее точку пересечения с плоскостью π. Решение:Через точку С проведем прямую, параллельную АВ. Через точку С′ проведем прямую, параллельную А′ В′. Точка Х пересечения этих прямых и будет искомой.

Используя этот метод, решим задачу на построение сечения куба.

Задача №4.Построить сечение куба плоскостью, проходящей через три точки А, В, С, принадлежащие попарно скрещивающимся ребрам этого куба. Решение:Найдем пересечение прямой АВ, лежащей в плоскости сечения, с плоскостью основания куба. Для этого построим параллельные проекции А′, В′ точек А, В на основании куба в направлении бокового ребра куба. Пересечение прямых АВ и А′В′ будет искомой точкой Р. Она принадлежит плоскости сечения и плоскости основания куба. Следовательно, плоскость сечения пересекает основание куба по прямой СР.

Точка пересечения этой прямой с ребром основания куба даст еще одну точку D сечения куба. Соединим точки С и D, B и D отрезками.

Через точку А проведем прямую, параллельную ВD, и точку ее пересечения с ребром кубам обозначим Е.

Соединим точки Е и С отрезком.

Через точку А проведем прямую, параллельную СD, и точку ее пересечения с ребром куба обозначим F.

Соединим точки В и F отрезком.

Многоугольник AECDBF и будет искомым изображением сечения куба плоскостью.

Закрепление изученного материала.

Самостоятельное решение задач с последующей проверкой.

Вариант 1. Какой фигурой является сечение куба А…D1 плоскостью, проходящей через вершины В1 и середину ребра СС1? Постройте сечение куба плоскостью, проходящей через три точки, расположенные так, как показано на рисунке.

Вариант 2. 1.Какой фигурой является сечение куба А…D1 плоскостью, проходящей через середины ребер АВ, ВС, и DD1? 2.Постройте сечение куба плоскостью, проходящей через три точки, расположенные так, как показано на рисунке.

Вопросы для самоконтроля:

1. В каком случае в сечение куба получается треугольник (равносторонний, равнобедренный, разносторонний)?

2. Какие четырехугольники могут получится в сечении куба плоскостью?

3. Может ли в сечении куба плоскостью получится правильный пятиугольник? Почему?

4. В каком случае в сечении куба плоскостью получится правильный шестиугольник?

5. Может ли в сечении куба получится четырехугольник изображенный на рисунке?

6. В чем заключается построение сечений методом «следов»?

Решить задачу:

Построить сечение куба плоскостью проходящей через точки М, N, К.

Рекомендуемая литература: