6. Содержание отчета

Отчет должен содержать:

1.Временные и спектральные диаграммы сигналов на входе и выходе дискретизатора при действии на входе:

• синусоидального колебания, частота которого меньше половины частоты дискретизации,

• синусоидального колебания, частота которого больше частоты дискретизации,

• случайной последовательности прямоугольных импульсов,

• сигнала, модулированного случайной последовательностью прямоугольных импульсов.

2. Выводы о влиянии частоты сигнала и частоты дискретизации на

• спектр дискретного сигнала,

• искажения аналогового сигнала, восстановленного из дискретного для всех видов сигналов на входе дискретизатора.

7. Методические указания по выполнению работы

Лабораторная работа выполняется в программной среде SCILAB. Откройте эту программу (Пуск-Программы-scilab-4.1.2- scilab-4.1.2). Появится основное окно приложения. Окно содержит меню, панель инструментов и рабочую область. Признаком того, что система готова к выполнению команды, является наличие знака приглашения (горизонтальной стрелки), после которого расположен мигающий курсор.

Щелчком левой кнопки мыши откройте редактор (Editor). Появится окно для редактирования. Из редактора откройте файл Diskret1 (File-Open-..Рабочий стол – ЦОС в Scilab – Diskret1). Текст программы приведён в Приложении Б. Появится текст программы с комментариями, которые вводятся с использованием знака //.

В строках 7-13 осуществляется ввод исходных данных для моделирования.

Затем в цикле по порядковому номеру расчетной точки i формируются

• аналоговая синусоида (строка 28),

• последовательность единичных отсчетов (строки 30-33),

• дискретная синусоида (строка 35).

Определяется спектр аналоговой (строка 38) и дискретной (строка 40) синусоид.

Для восстановления аналоговой синусоиды из дискретной сначала находится номер гармоники спектра k1, соответствующий половине частоты дискретизации (строка 42).

Затем из отсчетов спектра дискретного сигнала sd с номерами k= 1,2,..k1 формируется спектр sv, соответствующий аналоговому сигналу (строки 43-49) , и путем обратного быстрого преобразования Фурье находится восстановленный аналоговый сигнал (строка 50).

Последующая часть программы обеспечивает построение временных и спектральных диаграмм.

Перед запуском программы рассчитайте по данным таблицы 1:

• частоту синусоидального сигнала F при первом из приведённых в таблице 1 значении количества расчетных точек в периоде синусоиды i_s,

• частоту дискретизации Fd,

• первые 5 частот спектральных составляющих спектра дискретной синусоиды.

Рассчитанные значения сведите в таблицу 4.

Таблица 4

Частота cоставляющей спектра дискретного сигнала	f1	f2	f3	f4	f5
Значение частоты при F= Fd =
Значение частоты при F= Fd =
Значение частоты при F= Fd =
Значение частоты при F= Fd =
Значение частоты при F= Fd =
Значение частоты при F= Fd =

Для выполнения пунктов 1.1-1.4 задания введите в программу исходные данные из таблицы 1, задав первое из приведённых значений параметра i_s.

Примечание: шаг изменения времени Δt в тексте программы обозначается как delta_t и его значение вводится без указания единиц измерения (см. приложение Б к лабораторной работе №1).

Сохраните программу (File-Save) и запустите её (Execute-Load into Scilab). Появится окно Scilab Graphic, подобное тому, что представлено на рисунке 1.

Рисунок 1

Убедитесь в том, что значения частот спектральных составляющих сигнала до и после дискретизации соответствуют выполненному расчету.

Повторите расчет и эксперимент при в 2 раза большем значении параметра i_s и значениях остальных параметров, указанных в таблице.

Результаты расчёта запишите в таблицу 4.

Запишите в отчет вывод о влиянии частоты сигнала на спектр дискретной синусоиды.

Повторите расчет и эксперимент при в 2 раза большем значении параметра i_d и значениях остальных параметров, указанных в таблице.

Результаты расчёта запишите в таблицу 4.

Запишите в отчет вывод о влиянии частоты дискретизации на спектр дискретной синусоиды.

Рассчитайте частоту синусоидального сигнала при втором значении параметра i_s, приведённом в таблице 1, и частоты первых пяти составляющих спектра дискретной синусоиды.

Результаты расчета запишите в таблицу 4.

Введите в программу исходные данные из таблицы 1 со вторым значением параметра i_s и запустите программу. Пронаблюдайте временные и спектральные диаграммы. Обратите внимание на то, что частота восстановленной синусоиды отличается от частоты аналоговой синусоиды.

Определите и запишите в отчет значение частоты восстановленной синусоиды.

Изменяя значение параметра i_s на относительно последнего значения, указанного в таблице 1, рассчитайте значения частот аналоговой синусоиды и частот первых пяти спектральных составляющих спектра дискретного сигнала. Запишите рассчитанные значения в таблицу 4.

Пронаблюдайте временные и спектральные диаграммы при изменённых значениях i_s.

Для выполнения п.2.1 - п.2.5 задания откройте программу Diskret2.sce (File-Open-..Рабочий стол – ЦОС в Scilab – Diskret2). Текст программы приведён в Приложении В. Эта программа отличается от предыдущей только видом сигнала, который подвергается дискретизации. Вместо синусоиды формируется случайная последовательность элементарных посылок – прямоугольных импульсов.

Формирование посылок осуществляется в цикле по порядковому номеру расчетной точки i.

Сначала моделируется последовательность единичных отсчётов I(i), период следования которых равен длительности элементарной посылки i_s (строки 30 – 33). Используемая при моделировании функция floor возвращает целую часть аргумента.

Затем на границе элементарной посылки при I(i)=1 проверяется значение случайной функции rand(1), которая выдаёт случайное число в интервале от нуля до единицы. Если rand(1) < 0.5, то элементарной посылке присваивается значение X_min, которое остаётся неизменным до появления следующего единичного отсчёта. В противном случае элементарной посылке присваивается значение X_max.

По исходным данным таблицы 2 рассчитайте значение частоты дискретизации и запишите его в отчет.

Введите в программу исходные данные из таблицы 2. Сохраните программу (File-Save) и запустите её (Execute-Load into Scilab).

Примечание: шаг изменения времени Δt в тексте программы обозначается как delta_t и его значение вводится без указания единиц измерения (см. приложение В к лабораторной работе №1).

Появится окно Scilab Graphic, подобное тому, что представлено на рисунке 2.

Сравните аналоговый сигнал, восстановленный из дискретного, с исходным аналоговым сигналом. Сравните спектры исходного аналогового и дискретного сигналов. Определите причину искажений восстановленного сигнала и укажите её в отчете.

Рисунок 2

Увеличьте значение параметра i_d в 2 раза, пронаблюдайте временные и спектральные диаграммы и запишите в отчет вывод о влиянии частоты дискретизации на искажения восстановленного сигнала.

Для выполнения п.3.1 - п.3.6 воспользуйтесь программой Diskret3.sce (Приложение Г). Эта программа отличается от предыдущей тем, что дискретизации подвергается модулированный сигнал x_s(i), а случайная последовательность элементарных посылок x(i) является модулирующим сигналом. Модуляция осуществляется путём умножения функции x(i) на функцию, описывающую синусоидальную несущую, (строка 41). В зависимости от вида модулирующего сигнала формируется сигнал или амплитудной, или фазовой манипуляции.

Предварительно рассчитайте частоту дискретизации F_d и частоту несущей f₀ модулированного аналогового сигнала, воспользовавшись значениями параметров i_d, i_s0 и Δt таблицы 3.

Рассчитайте частоты спектра дискретного сигнала, соответствующие частоте аналоговой несущей и запишите значения 5 частот, начиная с минимальной, в таблицу 5 в порядке их возрастания.

Таблица 5

Частота несущей в спектре дискретного сигнала	f01	f02	f03	f04	f05
Значение частоты при f0= Fd =
Значение частоты при f0= Fd =
Значение частоты при f0= Fd =

Изменив значение параметра i_s0 на 10%, заполните следующие две строки таблицы 5.

Введите в программу Diskret3 значения параметров из таблицы 3 и запустите программу.

Примечание: шаг изменения времени Δt в тексте программы обозначается как delta_t и его значение вводится без указания единиц измерения (см. приложение Г к лабораторной работе №1).

Появится окно Scilab Graphic, подобное тому, что представлено на рисунке 3, при фазовой модуляции или подобное тому, что приведено на рисунке 4, при амплитудной модуляции.

Обратите внимание на равномерность сгустков спектра дискретного сигнала и на отличие частоты несущей восстановленного сигнала от частоты несущей модулированного сигнала на входе дискретизатора. Сравните рассчитанные частоты с размноженными в процессе дискретизации частотами несущей аналогового сигнала сигнала.

Увеличьте параметр i_s0 на 10% и повторите эксперимент. Обратите внимание на распределение сгустков спектра дискретного сигнала вдоль оси частот и искажения восстановленного сигнала.

Уменьшите параметр i_s0 на 10% и повторите эксперимент. Обратите внимание на распределение сгустков спектра дискретного сигнала вдоль оси частот.

В отчет запишите вывод о влиянии частоты несущей аналогового сигнала на искажения аналогового сигнала, восстановленного из дискретного.

Рисунок 3

Рисунок 4

Приложение А

к лабораторной работе №1

Дискретизация непрерывных сигналов

1. Спектр дискретной косинусоиды. Эффект размножения спектра

Дискретизацией называется замена непрерывного сигнала дискретными отсчетными значениями (отсчетами), взятыми через определенный интервал времени - интервал дискретизации T_Д.

На рисунке 1 показаны косинусоидальный сигнал x(t) и вспомогательное колебание u(t), представляющее последовательность коротких прямоугольных импульсов с периодом T_Д и длительностью .

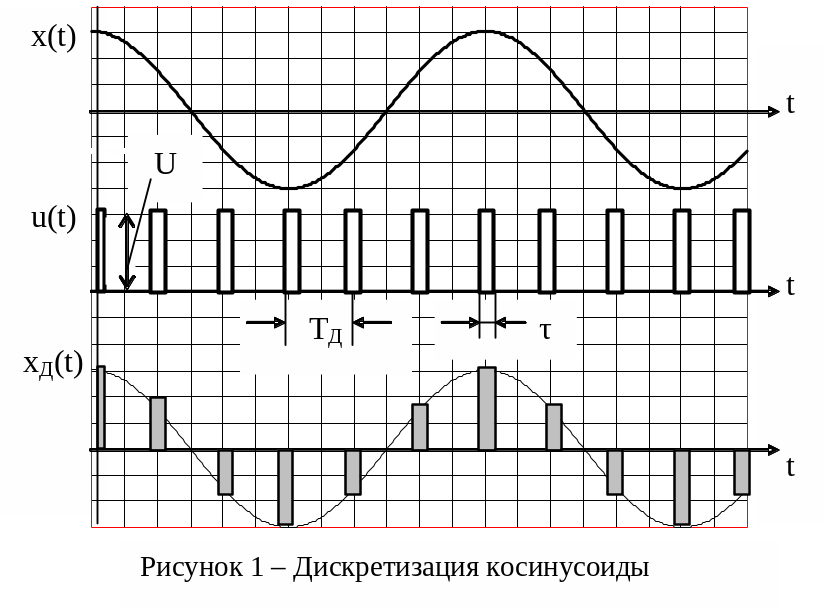
Дискретный сигнал с математической точки зрения можно рассматривать как результат перемножения функций и .

Периодическая функция u(t) может быть представлена рядом Фурье

(1)

где С₀ и С_k - коэффициенты ряда Фурье, определяемые следующими соотношениями:

, ,

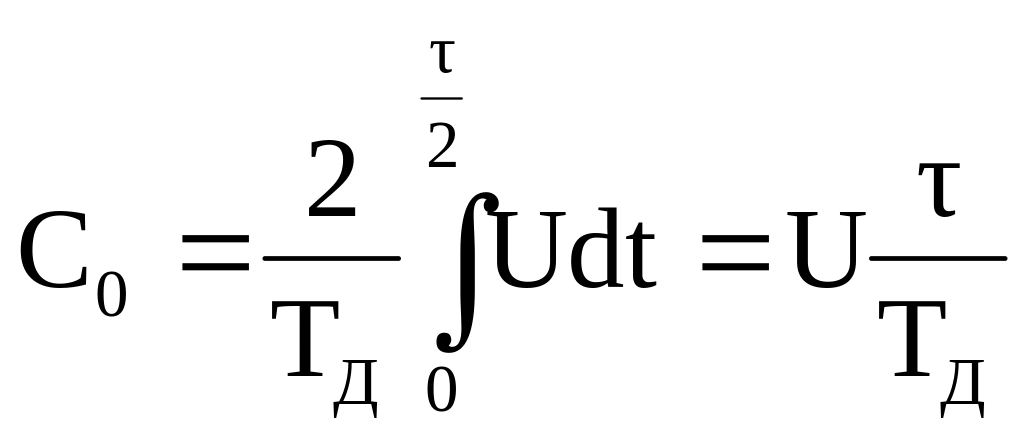- частота дискретизации.

После подстановки последних соотношений в (1) получим

. (2)

Из (2) видно, что амплитуда k-ой гармоники вспомогательного колебания u(t) пропорциональна функции sin(x)/x, где x = k π τ / T_Д. При x = 0 эта функция равна единице. Первый нуль функции имеет место при x = π. Это означает, что при τ / T_Д = 0.001 амплитуда 1000-ой гармоники равна нулю. Однако при амплитуда k-ой гармоники отличается от амплитуды первой гармоники не более чем на 1.6%.

В этом случае можно воспользоваться приближенным соотношением

(3)

При сигнал на выходе дискретизатора определяется соотношением

(4)

Из него видно, что спектр дискретной косинусоиды содержит спектральную составляющую на частоте входного аналогового сигнала и бесконечное множество составляющих на частотах . Причем амплитуды всех спектральных составляющих в пределах сделанного допущения одинаковы и пропорциональны амплитуде входного аналогового сигнала. Амплитудный спектр аналогового и дискретного косинусоидальных сигналов показан на рисунке 2.

Рисунок 2 – Спектр косинусоиды до (а) и после (б) дискретизации

Из рисунка видно, что в результате дискретизации возникает размножение спектра аналогового сигнала.

Спектр дискретной косинусоиды представляет собой периодическую функцию частоты, период которой равен частоте дискретизации.

2. Дискретизация периодического аналогового сигнала с ограниченным спектром. Эффект наложения спектров. Выбор частоты дискретизации

Пусть сигнал x(t) представляет собой периодическую функцию времени с периодом Т и с ограниченным спектром, которая может быть представлена рядом Фурье

, (5)

где с₀ – постоянная составляющая сигнала, a_i и b_i – коэффициенты ряда Фурье для функций синуса и косинуса соответственно

, , ,

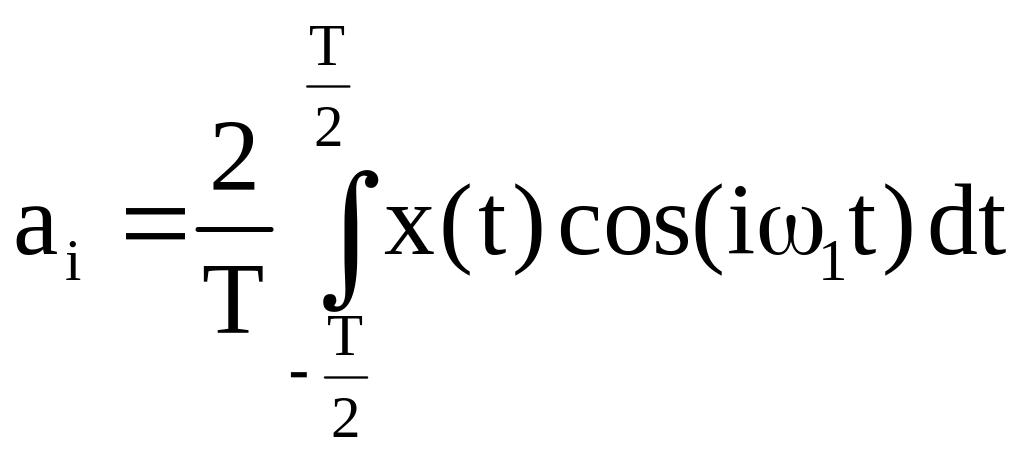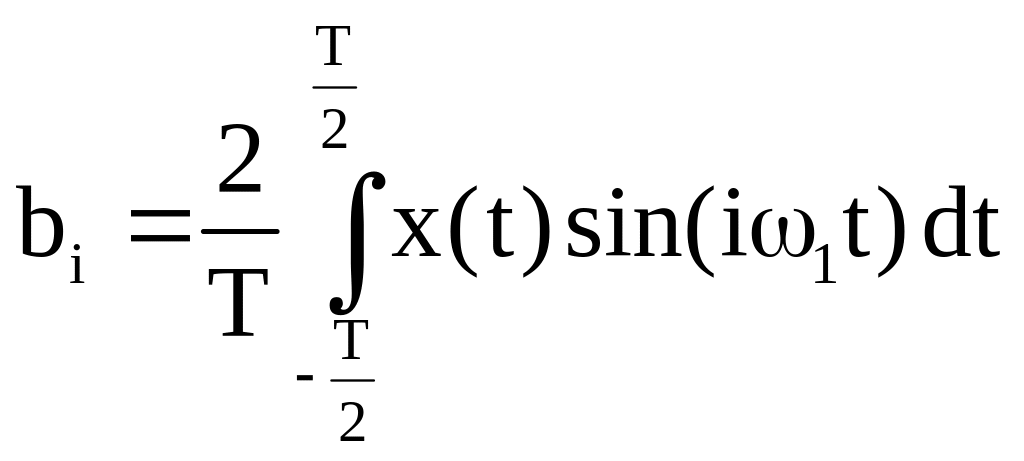ω₁ – частота первой гармоники сигнала, iω₁ – частота i-ой гармоники, I – максимальный номер гармоники.

Амплитуда и фаза i –ой гармоники определяются следующими соотношениями:

.

Зависимость c_i от частоты представляет собой амплитудный спектр сигнала, а зависимость φ_i от частоты – его фазовый спектр.

Учитывая последние соотношения, представим (5) в виде суммы гармоник с амплитудами c_i и фазами φ_i

при _.

Определим дискретный сигнал

Последнее соотношение определяет спектр после дискретизации периодического аналогового сигнала с ограниченным спектром. Из него видно:

1. В спектре дискретного сигнала присутствуют все составляющие спектра аналогового сигнала с частотами iω₁ (первое слагаемое). Амплитуды этих спектральных составляющих пропорциональны соответствующим амплитудам спектральных составляющих аналогового сигнала (коэффициент пропорциональности - Uτ / T_Д).

2. В спектре дискретного сигнала имеются сгустки спектральных составляющих вблизи частот kω_Д (второе слагаемое). Амплитуды этих спектральных составляющих пропорциональны соответствующим амплитудам спектральных составляющих аналогового сигнала (коэффициент пропорциональности - Uτ / T_Д). Период следования сгустков спектра равен частоте дискретизации.

На рисунке 3 показан амплитудный спектр аналогового периодического сигнала до и после дискретизации при двух разных значениях частоты дискретизации.

В спектре сигнала до дискретизации присутствуют 3 спектральные составляющие с частотами F₁=ω₁ /(2π), 2F₁, F_max=5F₁. Чтобы сформировать спектр дискретного сигнала нужно для каждой из этих составляющих найти составляющие спектра дискретного сигнала, которые она порождает, как при нахождении спектра дискретной косинусоиды. При этом нужно учитывать значение амплитуды исходной составляющей спектра аналогового сигнала. Результирующий спектр находится методом суперпозиции.

Из рисунка 3б видно, что если из спектра дискретного сигнала выделить составляющие, соответствующие спектру исходного аналогового сигнала, то таким образом можно восстановить аналоговый сигнал из дискретного. Такую селекцию можно осуществить с помощью фильтра, АЧХ которого показана на рисунке.

Рисунок 3 – Спектр периодического аналогового сигнала до дискретизации (а), после дискретизации при F_Д>2F_max (б), после дискретизации при F_Д<2F_max (в)

В восстановленном сигнале будут отсутствовать искажения, если

• АЧХ фильтра равномерна,

• ФЧХ линейна в диапазоне частот от F₁ до F_max,

• коэффициент передачи равен нулю на частотах .