2.2 Методический инструментарий оценки стоимости денег во времени.
Учет фактора времени осуществляется с помощью специальных методов (операций) наращения и дисконтирования, в основу которых положена техника процентных вычислений. Сущностью этих методов является приведение денежных сумм, относящихся к различным временным периодам к требуемому моменту времени в настоящем или будущем. В качестве нормы приведения используется процентная ставка.
Брикхэм Ю. и Эрхардт М. определяют процесс наращения (compounding) «как процесс перехода от текущей (приведенной) стоимости (present value, PV), к будущей стоимости (future value, FV)»1, а дисконтирование (discounting) определяет как процесс «определения текущей (приведенной) стоимости»2. Из отечественных авторов, Ковалев В.В. дает следующее определение: «Процесс, в котором заданы исходная сумма (PV) и ставка (процентная или учетная), в финансовых вычислениях называется наращением, искомая величина – наращенной суммой, а используемая в операции ставка – ставкой наращения. Процесс, в котором заданы ожидаемая в будущем к получению (возвращаемая) сумма (FV) и ставка, называется дисконтированием, искомая величина – дисконтированной суммой (иногда используется термин приведенная сумма), а используемая в операции ставка – ставкой дисконтирования».3 Аналогичное определение дает Бланк И.А. и другие.
В зависимости от условий проведения финансовых операций как наращение (будущая стоимость), так и дисконтирование (приведенная стоимость) могут осуществляться с применением простых и сложных процентов.
Формула для вычисления простых процентов имеет следующий вид
(5)
где PV – основная или исходная сумма, заимствованная (или одолженная) в первоначальный момент времени (в точке (о) в начале первого периода),
r – процентная ставка за один период времени,
n – количество периодов времени.
Если продолжительность
краткосрочной операции меньше года
(т.е. t
), то
(6)
Т - число календарных дней периода, на который установлена процентная ставка (годовая – 360 дней, месячная – 30 дней)
t – длительность финансовой операции в днях
Дисконтирование (встречается название математическое дисконтирование) предполагает, что в качестве нормы приведения используют ставку r , применяемую при наращении. Т.о. математическое дисконтирование представляет собой задачу, обратную наращению (см. выше) и сводится к определению PV по известным значениям FV, r, n .
Из зависимости
(5)
(7)
Из зависимости
(6)
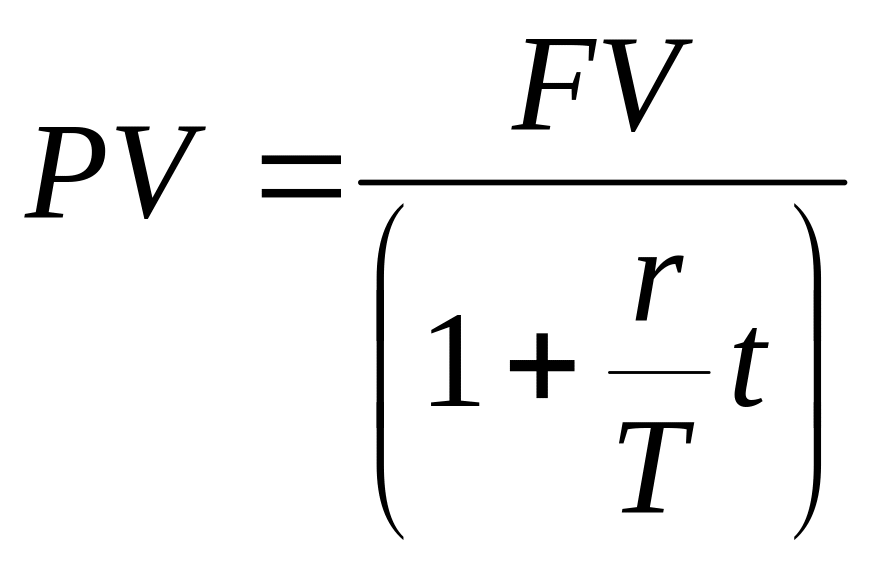(8)
Большинство операций в финансах, связанных со стоимостью денег во времени не имеет вообще никакого отношения к простым процентам. Обычно в таких ситуациях используются сложные проценты.
Чтобы определить будущую (конечную) стоимость, расчет делают по следующим формулам.
Если проценты начисляются один раз в год:
(9)
Данная формула является базовой, описывающей накопленную сумму единицы.
Период накопления может быть и более коротким, чем год, например, месяц, квартал, полугодие (т.е.m-раз в год).
Если проценты начисляются m - раз в год
(10)
Определение текущей стоимости единицы (приведенной стоимости или дисконтирование) - действие обратное начислению сложных процентов.
из зависимости
(9)
(11)
из зависимости
(10),
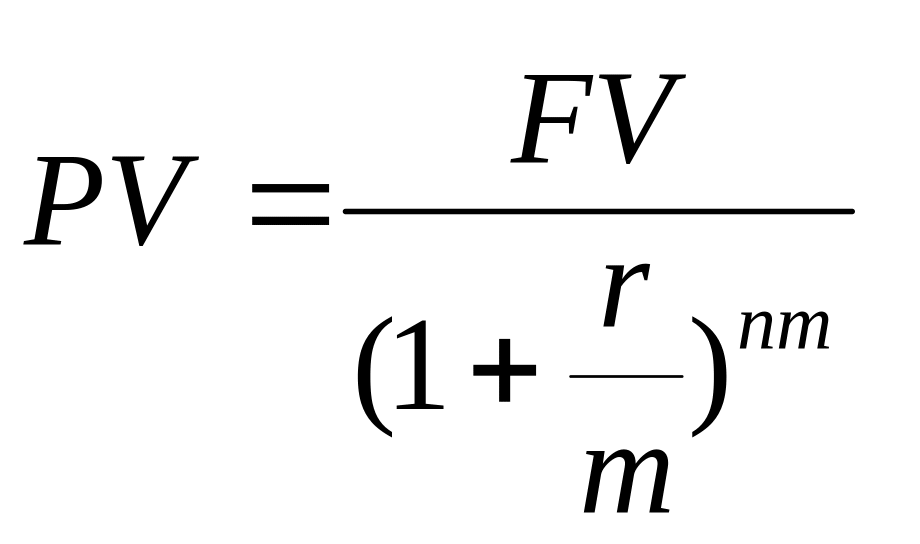(12)
Решение задач
1. Сделан вклад в банк на депозит в сумме 100000 д.ед. под 19% годовых сроком на три месяца. Определить размер вклада к концу срока.
Решение. Размер вклада = 100000×[1 + (0,19/360×90)] = 104750 д.ед.
2. Заемщик получил кредит на 6 месяцев под 23% годовых с условием вернуть 200000 д.ед. Какую сумму получил заемщик в момент заключения договора.
Решение. Полученная заемщиком сумма = 200000/(1 + 0,23/360×180) = 179372 д.ед.
3. Выдана ссуда в размере 350000 д.ед. на 1 год под 11% годовых. Определить размер платежа к погашению.
Решение. Размер платежа = 350000×(1 + 0,11×1) = 388500 д.ед.
4. Кредит в размере 100000 д.ед. выдан под сложные проценты по ставке 20% годовых сроком на 2 года. Найти полную сумму долга к концу срока.
Решение. Сумма долга = 100000×(1 + 0,2)2 = 144000 д.ед.
5. Сделан вклад в банк в сумме 250000 д.ед. Срок вклада 24 месяца. Годовая процентная ставка 15%, проценты сложные и начисляются по полугодиям. Определить наращенную сумму к концу срока.
Решение. Наращенная сумма = 250000(1 + 0,15/2)4 = 333867 д.ед.
6. В контракте предусматривается погашение обязательств в сумме 110 тыс. руб. через 120 дней. Первоначальная сумма долга 90 тыс. руб. определить доходность ссудной операции для кредитора в виде ставки процента.
Решение. Доходность = [(110 – 90)×360] / (90×120) = 0, 6667 или 66,67%
7. Выдана ссуда в размере 5000 тыс. д.ед. на 1 месяц под 16% годовых. Определить размер платежа к погашению.
Решение. Размер платежа = 5000× [1+(0,16×30/360)] = 5066, 7 тыс. д.ед.
8. Сделан вклад в банк на депозит в сумме 5000 тыс. д.ед. под простые проценты по ставке 25% годовых сроком на 2 года. Определить величину вклада в конце срока.
Решение. Величина вклада = 5000×(1 + 0,25×2) = 7500 тыс. д.ед.
9. Банк выдал ссуду в размере 150 тыс. д.ед. сроком на 5 месяцев под проценты по ставке 11% в месяц. Рассчитать наращенное значение долга.
Решение. Наращенное значение долга = 150×[1+(0,11×150/30)] = 232,5 тыс.д.ед.
10. Сделан вклад в банк на 2 года в сумме 20000 д.ед. по сложной процентной ставке 30% годовых. Проценты начисляются раз в квартал Какова величина в клада к концу срока.
Решение. Величина вклада = 20000× (1 + 0,3/4)8 = 35669,6 д.ед.